8. laborgyakorlat
Numerikus számítások fizikusoknak
Az anyag bizonyos részei nem publikálódnak html formátumba. Ezek a részek kikommentelve szerepelnek a fájlban.
Contents
clear all, close all
Adatbekérés
Szöveg vagy szám bekérése.
%{ n=input('Adjunk egy egész számot! '); n/2 pause nev=input('Mi a neve? '); nev % A szöveget karakterláncként tárolja a matlab. whos nev %}
Grafikus adatbekérés.
%{ ezplot(@sin) pontok=ginput(4) hold on plot(pontok(:,1),pontok(:,2)) %}
Szöveg kiírása a képernyőre
A disp paranccsal egyszerű szöveget irathatunk ki a képernyőre, formázási lehetőség nélkül. Formázott szöveget az fprintf paranccsal tudunk a képernyőre írni.
Egy karakterlánc kiírása a képernyőre.
disp('Az A mátrix:')
A=[1,2;3,4];
disp(A)
Az A mátrix:
1 2
3 4
Több karakterláncot vektorba kell foglalni, a mátrixokat karaktereket tartalmazó mátrixba kell konvertálni a num2str paranccsal. Itt is figyelni kell a karakterekből álló mátrixok méretére!
num2str(A) % disp(['Az A mátrix:',num2str(A),' alakú.']) % hibaüzenetet adna disp(['Az A mátrix első sora: ', num2str(A(1,:)),' alakú.']) whos
ans = 1 2 3 4 Az A mátrix első sora: 1 2 alakú. Name Size Bytes Class Attributes A 2x2 32 double ans 2x4 16 char
Formázott kiírás az fprintf paranccsal. fprintf(szöveg formázójelekkel, a formázójelek által meghatározott változók felsorolása) Az általában használt formázások f (fixpontos), e (normál alak), g (a kettő közül a rövidebb), \n új sor, \t tabuláció, \b backspace. %a.bf: a: a kiírt karakterek minimális száma, b: tizedesjegyek száma Lásd bővebben a Matlab helpjét!
x=sqrt(2); y=-sqrt(2); fprintf('Az egyenlet egyik megoldása %f,\na másik %f.\n',x,y) fprintf('Az egyenlet egyik megoldása %10.2f,\na másik %10.2e.\n',x,y) fprintf('A hiba %4.2f%%-os\n',x)
Az egyenlet egyik megoldása 1.414214, a másik -1.414214. Az egyenlet egyik megoldása 1.41, a másik -1.41e+000. A hiba 1.41%-os
Példa: egész számok és négyzeteik.
fprintf(' i i^2\n') for i=1:10 fprintf('%2.0f %4.0f\n',i,i^2) end
i i^2 1 1 2 4 3 9 4 16 5 25 6 36 7 49 8 64 9 81 10 100
Hibaüzenet a képernyőre
% error('Hiba történt') % Figyelmeztető hangjelzés beep
Elágazások
if elágazás
x=15; if x<16 beep % a felhasználó figyelmeztetése disp('A zh sikertelen.') else % opcionális disp('A zh sikeres.') end
A zh sikertelen.
elseif elágazás
pont=25; if pont<16 beep % a felhasználó figyelmeztetése disp('A gyakjegy ''elégtelen''.') elseif pont<55 disp('A gyakjegy ''elégséges''.') elseif pont<70 disp('A gyakjegy ''közepes''.') elseif pont<85 disp('A gyakjegy ''jó''.') else disp('A gyakjegy ''jeles''.') end
A gyakjegy 'elégséges'.
Switch/case elágazás
jegy=3; switch jegy case 1 beep disp('Elégtelen') case 2 disp('Elégséges') case 3 disp('Közepes') case 4 disp('Jó') case 5 disp('Jeles, gratulálok!') otherwise % opcionális error('Ilyen jegy nincs, adjon meg másikat!') % hibaüzenet írása end
Közepes
Példa
%{ cel=input('Budapestre vagy Szegedre szeretne utazni (''B''/''S'')?: '); switch cel case 'B' disp('2855 Ft') case 'S' disp('5680 Ft') otherwise disp('Helytelen település') end %}
Nemlineáris egyenletek megoldása (egyváltozós eset)
fzero parancs
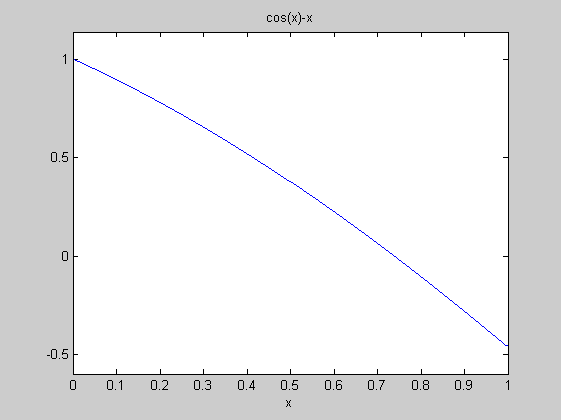
f=@(x)cos(x)-x; ezplot(f,[0,1]) fzero(f,0.6) % közelítő zérushely pause fzero(f,[0.5,0.8]) % előjelváltó intervallum pause [x,ertek,flag]=fzero(f,0.6)
ans =
0.739085133215161
ans =
0.739085133215161
x =
0.739085133215161
ertek =
0
flag =
1
Hátrányok - rossz eredményt ad
fzero(@tan,2)
ans = 1.570796326794896
A zérushelykeresési paraméterek beállítása.
% optimset('fzero') % Megnézi a jelenlegi paraméterbeállítást % pause options=optimset('Display','iter','TolFun',10^-8) fzero(f,0.6,options)
options =
Display: 'iter'
MaxFunEvals: []
MaxIter: []
TolFun: 1.000000000000000e-008
TolX: []
FunValCheck: []
OutputFcn: []
PlotFcns: []
ActiveConstrTol: []
Algorithm: []
AlwaysHonorConstraints: []
BranchStrategy: []
DerivativeCheck: []
Diagnostics: []
DiffMaxChange: []
DiffMinChange: []
FinDiffType: []
GoalsExactAchieve: []
GradConstr: []
GradObj: []
HessFcn: []
Hessian: []
HessMult: []
HessPattern: []
HessUpdate: []
InitialHessType: []
InitialHessMatrix: []
InitBarrierParam: []
InitTrustRegionRadius: []
Jacobian: []
JacobMult: []
JacobPattern: []
LargeScale: []
LevenbergMarquardt: []
LineSearchType: []
MaxNodes: []
MaxPCGIter: []
MaxProjCGIter: []
MaxRLPIter: []
MaxSQPIter: []
MaxTime: []
MeritFunction: []
MinAbsMax: []
NodeDisplayInterval: []
NodeSearchStrategy: []
NonlEqnAlgorithm: []
NoStopIfFlatInfeas: []
ObjectiveLimit: []
PhaseOneTotalScaling: []
Preconditioner: []
PrecondBandWidth: []
RelLineSrchBnd: []
RelLineSrchBndDuration: []
ScaleProblem: []
ShowStatusWindow: []
Simplex: []
SubproblemAlgorithm: []
TolCon: []
TolConSQP: []
TolGradCon: []
TolPCG: []
TolProjCG: []
TolProjCGAbs: []
TolRLPFun: []
TolXInteger: []
TypicalX: []
UseParallel: []
Search for an interval around 0.6 containing a sign change:
Func-count a f(a) b f(b) Procedure
1 0.6 0.225336 0.6 0.225336 initial interval
3 0.583029 0.251769 0.616971 0.198664 search
5 0.576 0.262648 0.624 0.187548 search
7 0.566059 0.277962 0.633941 0.171758 search
9 0.552 0.299477 0.648 0.149293 search
11 0.532118 0.329617 0.667882 0.117253 search
13 0.504 0.371658 0.696 0.0714129 search
15 0.464235 0.429929 0.735765 0.00555337 search
17 0.408 0.509916 0.792 -0.0895768 search
Search for a zero in the interval [0.408, 0.792]:
Func-count x f(x) Procedure
17 0.792 -0.0895768 initial
18 0.734622 0.00746157 interpolation
19 0.739034 8.5067e-005 interpolation
20 0.739085 -3.23665e-009 interpolation
21 0.739085 3.64153e-014 interpolation
22 0.739085 0 interpolation
Zero found in the interval [0.408, 0.792]
ans =
0.739085133215161