8. laborgyakorlat, házik megoldásai

Contents

clear all, close all

1. feladat

q0=10; R=50; L=5; C=1e-4;
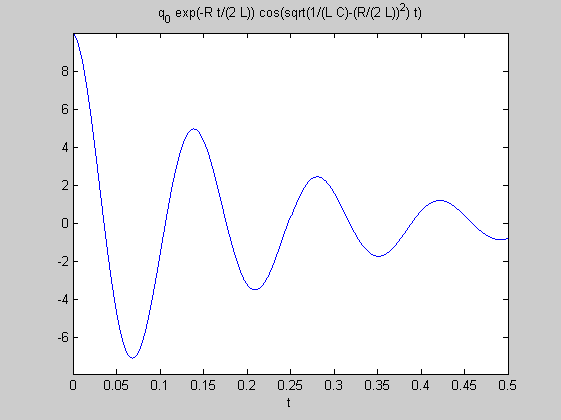
q=@(t)q0*exp(-R*t/(2*L))*cos(sqrt(1/(L*C)-(R/(2*L))^2)*t);
disp('A töltés alakulása a [0,0.5] időintervallumon.')
ezplot(q,[0,0.5])

A töltés alakulása a [0,0.5] időintervallumon.

2. feladat

n=20; P=4; r=1+P/100;
B=4;
n=1:25;
A=B*(r-1)*r.^n./(r.^n-1);
C=A.*n/B*100;
fprintf('Futamidő (mFt) Törlesztő (mFt) Visszafizetés (%%)\n')
for i=1:25
fprintf('%2.0f          %8.4f           %8.4f\n',n(i),A(i),C(i))
end

pause
% vagy mert több oszlop esetén oszloponként hajtja végre a Matlab a kiírást
fprintf('Futamidő (mFt) Törlesztő (mFt) Visszafizetés (%%)\n')
fprintf('%2.0f          %8.4f           %8.4f\n',[n;A;C])

Futamidő (mFt) Törlesztő (mFt) Visszafizetés (%)
 1            4.1600           104.0000
 2            2.1208           106.0392
 3            1.4414           108.1046
 4            1.1020           110.1960
 5            0.8985           112.3136
 6            0.7630           114.4571
 7            0.6664           116.6267
 8            0.5941           118.8223
 9            0.5380           121.0437
10            0.4932           123.2909
11            0.4566           125.5639
12            0.4262           127.8626
13            0.4006           130.1868
14            0.3787           132.5366
15            0.3598           134.9117
16            0.3433           137.3120
17            0.3288           139.7375
18            0.3160           142.1880
19            0.3046           144.6634
20            0.2943           147.1635
21            0.2851           149.6882
22            0.2768           152.2374
23            0.2692           154.8108
24            0.2623           157.4084
25            0.2560           160.0299
Futamidő (mFt) Törlesztő (mFt) Visszafizetés (%)
 1            4.1600           104.0000
 2            2.1208           106.0392
 3            1.4414           108.1046
 4            1.1020           110.1960
 5            0.8985           112.3136
 6            0.7630           114.4571
 7            0.6664           116.6267
 8            0.5941           118.8223
 9            0.5380           121.0437
10            0.4932           123.2909
11            0.4566           125.5639
12            0.4262           127.8626
13            0.4006           130.1868
14            0.3787           132.5366
15            0.3598           134.9117
16            0.3433           137.3120
17            0.3288           139.7375
18            0.3160           142.1880
19            0.3046           144.6634
20            0.2943           147.1635
21            0.2851           149.6882
22            0.2768           152.2374
23            0.2692           154.8108
24            0.2623           157.4084
25            0.2560           160.0299

3. feladat

% A=input('Adjunk meg egy mátrixot! ');
A=[1,2;3,4]
s=size(A);
if s(1)==s(2)
    disp('Négyzetes')
else
    disp('Nem négyzetes')
end

A =
     1     2
     3     4
Négyzetes

4. feladat

%{
nev=input('Mi a neved? ','s');
disp(['Helló ',nev,'!'])
%}

5. feladat

% g=input('Adjuk meg a gravitációs gyorsulást! ')
g=9.81;
% t0=input('Adjuk meg a kezdő időpontot! ')
t0=10;
% t1=input('Adjuk meg a záró időpontot! ')
t1=100;
t=linspace(t0,t1,10);
s=g*t.^2/2;
disp([num2str(g),' gyorulás mellett az alábbi helyadatokat kapjuk:'])
fprintf('  Idő (s)      Hely (m)        \n')
for i=1:10
fprintf('  %10.2f    %10.4f        \n',t(i),s(i))
end

pause
% vagy mert több oszlop esetén oszloponként hajtja végre a Matlab a kiírást
fprintf('  Idő (s)      Hely (m)        \n')
fprintf('  %8.2f    %10.4f        \n',[t;s])

9.81 gyorulás mellett az alábbi helyadatokat kapjuk:
  Idő (s)      Hely (m)        
       10.00      490.5000        
       20.00     1962.0000        
       30.00     4414.5000        
       40.00     7848.0000        
       50.00    12262.5000        
       60.00    17658.0000        
       70.00    24034.5000        
       80.00    31392.0000        
       90.00    39730.5000        
      100.00    49050.0000        
  Idő (s)      Hely (m)        
     10.00      490.5000        
     20.00     1962.0000        
     30.00     4414.5000        
     40.00     7848.0000        
     50.00    12262.5000        
     60.00    17658.0000        
     70.00    24034.5000        
     80.00    31392.0000        
     90.00    39730.5000        
    100.00    49050.0000        

6. feladat

7. feladat

8. feladat

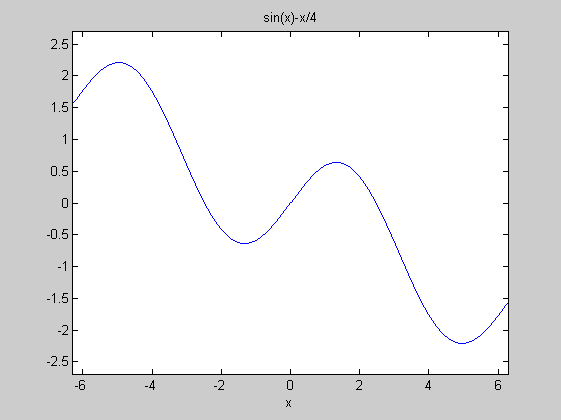
f=@(x)sin(x)-x/4;
ezplot(f)
fzero(f,[2,4])

ans =
   2.474576787369829

9. feladat

P=10^4; T=340; a=364; b=0.03; R=1.618;
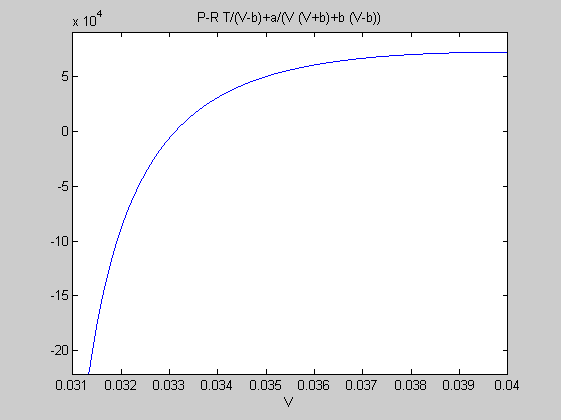
f=@(V)P-R*T/(V-b)+a/(V*(V+b)+b*(V-b));
ezplot(f,[0.031,0.04])
fzero(f,[0.031,0.04])
f(ans)

ans =
   0.033112854261202
ans =
    5.820766091346741e-011

10. feladat

% pl.
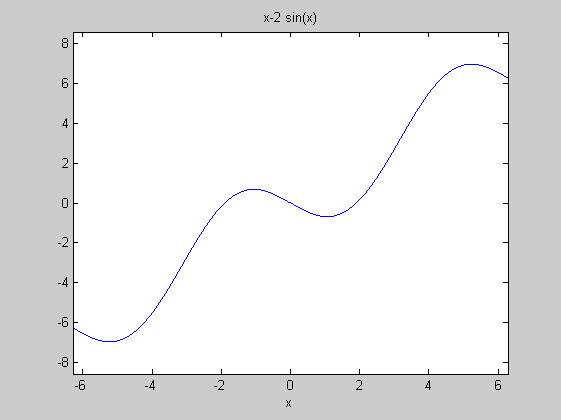
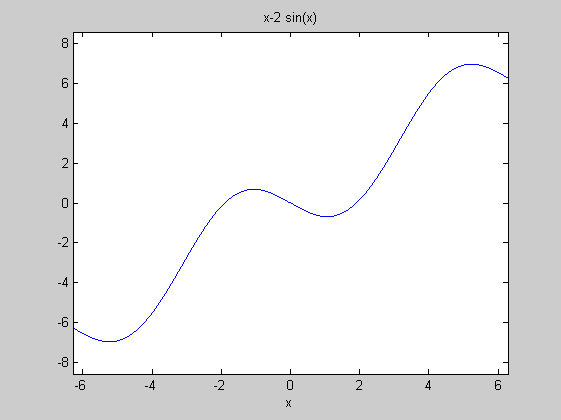
f=@(x)x-2*sin(x);
ezplot(f)
zh=fzero(f,2)
disp(['Három zérushely van: 0, ',num2str(-zh),', ',num2str(zh)])

zh =
   1.895494267033981
Három zérushely van: 0, -1.8955, 1.8955

11. feladat

% pl.
f=@(x)x-2*sin(x);
fd=@(x)1-2*cos(x);
ezplot(f)
disp('2.5-ről indítható a Newton-módszer')
fprintf('lépés         x\n')
x=2.5;
for i=1:8
    x=x-f(x)/fd(x);
    fprintf('%2.0f     %16.14f\n',i,x)
end

2.5-ről indítható a Newton-módszer
lépés         x
 1     1.99926522475217
 2     1.90092359542913
 3     1.89551119515304
 4     1.89549426719978
 5     1.89549426703398
 6     1.89549426703398
 7     1.89549426703398
 8     1.89549426703398

Published with MATLAB® 7.6