9. laborgyakorlat

Numerikus számítások fizikusoknak

Contents

clear all, close all

Newton-iteráció egyenletrendszerre

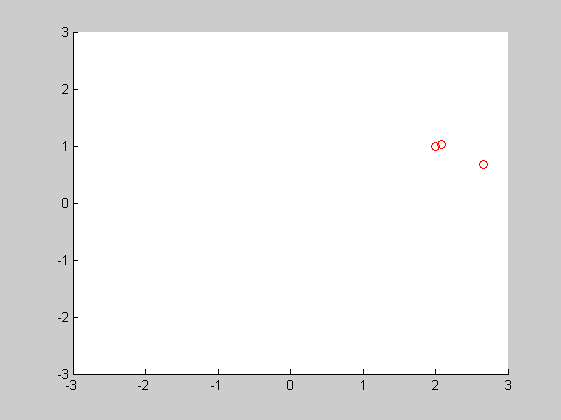
close all
F=@(x)[x(1).^2+x(2)-5;x(1)+x(2).^2-3]
J=@(x)[2*x(1),1;1,2*x(2)];

x=[1;1];
hold on
for i=1:10
    x=x-J(x)\F(x)
    plot(x(1),x(2),'ro')
    axis([-3,3,-3,3])
    pause
end
hold off

F = 
    @(x)[x(1).^2+x(2)-5;x(1)+x(2).^2-3]
x =
    2.6667
    0.6667
x =
    2.0788
    1.0242
x =
    2.0016
    0.9995
x =
    2.0000
    1.0000
x =
    2.0000
    1.0000
x =
    2.0000
    1.0000
x =
    2.0000
    1.0000
x =
    2.0000
    1.0000
x =
    2.0000
    1.0000
x =
    2.0000
    1.0000

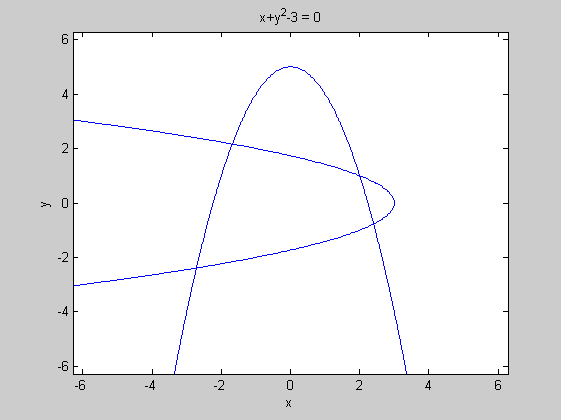
Implicit függvények ábrázolása segíthet

ezplot('x^2+y-5')
hold on
ezplot('x+y^2-3')

Nemlineáris egyenletrendszerek megoldása (optimization toolbox)

Az fsolve parancs alkalmazása

F=@(x)[x(1).^2+x(2)-5;x(1)+x(2).^2-3]
[x,f,flag]=fsolve(F,[0 1])
fsolve(F,[0 1],optimset('TolFun',10^-15,'TolX',10^-10,'MaxIter',600))

F = 
    @(x)[x(1).^2+x(2)-5;x(1)+x(2).^2-3]
Optimization terminated: first-order optimality is less than options.TolFun.
x =
    2.0000    1.0000
f =
  1.0e-006 *
    0.0070
    0.3399
flag =
     1
Optimization terminated: first-order optimality is less than options.TolFun.
ans =
     2     1

Interpolációs feladatok megoldása

interp1, polyfit, polyval, polyder, polyint parancsok

Egyváltozós függvények interpolációja

interp1 - alapértelmezés szakaszonkét lineáris 'spline' - szakaszonként spline 'pchip' - alakmegőrző

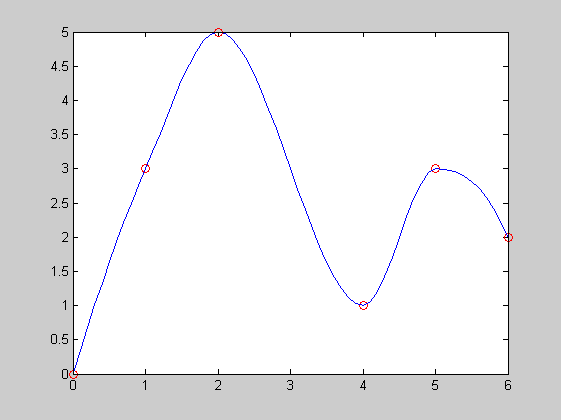
close
x=[0,1,2,4,5,6]
y=[0,3,5,1,3,2]
plot(x,y,'ro')
interp1(x,y,4.5)
xx=0:0.1:6;
yy=interp1(x,y,xx);
hold on
plot(xx,yy,'b-')

close
x=[0,1,2,4,5,6]
y=[0,3,5,1,3,2]
plot(x,y,'ro')
interp1(x,y,4.5,'spline')
xx=0:0.1:6;
yy=interp1(x,y,xx,'spline');
hold on
plot(xx,yy,'b-')

close
x=[0,1,2,4,5,6]
y=[0,3,5,1,3,2]
plot(x,y,'ro')
interp1(x,y,4.5,'pchip')
xx=0:0.1:6;
yy=interp1(x,y,xx,'pchip');
hold on
plot(xx,yy,'b-')

x =
     0     1     2     4     5     6
y =
     0     3     5     1     3     2
ans =
     2
x =
     0     1     2     4     5     6
y =
     0     3     5     1     3     2
ans =
    1.7813
x =
     0     1     2     4     5     6
y =
     0     3     5     1     3     2
ans =
     2

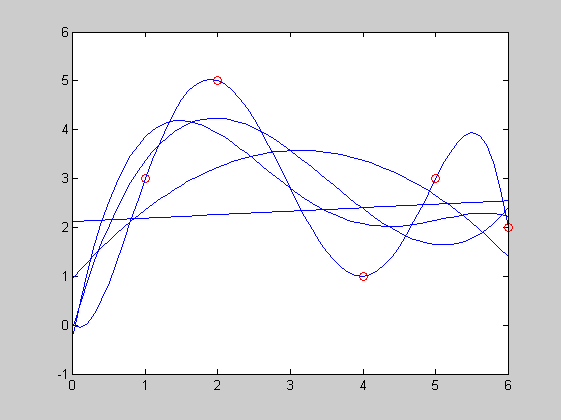
Egyváltozós polinomillesztés

polyfit, polyval

close
x=[0,1,2,4,5,6]
y=[0,3,5,1,3,2]
plot(x,y,'ro')
xx=0:0.1:6;
hold on
for i=1:5
polinom=polyfit(x,y,i);
yy=polyval(polinom,xx);
plot(xx,yy,'b-')
pause
end

x =
     0     1     2     4     5     6
y =
     0     3     5     1     3     2

polider, polyint parancsok

polyder([1,0,0])
polyint([1,0,0])

ans =
     2     0
ans =
    0.3333         0         0         0

Published with MATLAB® 7.6