9. laborgyakorlat, házik megoldásai

Contents

clear all, close all

1. feladat

% pl. az első egyenletrendszerre

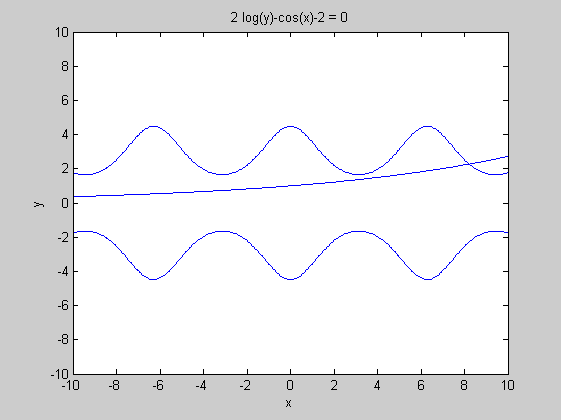
ezplot('exp(x/10)-y',[-10,10])
hold on
ezplot('2*log(y)-cos(x)-2',[-10,10])
hold off

f=@(x)[exp(x(1)/10)-x(2);2*log(x(2))-cos(x(1))-2]
J=@(x)[exp(x(1)/10)/10,-1;sin(x(1)),2/x(2)]

x=[8;2]
for i=1:10
    x=x-J(x)\f(x)
end

fsolve(f,[8,2])

f = 
    @(x)[exp(x(1)/10)-x(2);2*log(x(2))-cos(x(1))-2]
J = 
    @(x)[exp(x(1)/10)/10,-1;sin(x(1)),2/x(2)]
x =
     8
     2
x =
    8.2002
    2.2701
x =
    8.2183
    2.2746
x =
    8.2183
    2.2747
x =
    8.2183
    2.2747
x =
    8.2183
    2.2747
x =
    8.2183
    2.2747
x =
    8.2183
    2.2747
x =
    8.2183
    2.2747
x =
    8.2183
    2.2747
x =
    8.2183
    2.2747
Optimization terminated: first-order optimality is less than options.TolFun.
ans =
    8.2183    2.2747

2. feladat

f=@(x)[x(1)+x(2)+x(3);x(1)^2+x(2)^2+x(3)^2-2;x(1)*(x(2)+x(3))+1];
J=@(x)[1,1,1;2*x(1),2*x(2),2*x(3);x(2)+x(3),x(1),x(1)]

fsolve(f,[1,1,1])

 x=[-1;0;1]
 for i=1:10
     x=x-J(x)\f(x)
 end

J = 
    @(x)[1,1,1;2*x(1),2*x(2),2*x(3);x(2)+x(3),x(1),x(1)]
Optimization terminated: first-order optimality is less than options.TolFun.
ans =
   -1.0000   -0.0000    1.0000
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1
x =
    -1
     0
     1

3. feladat

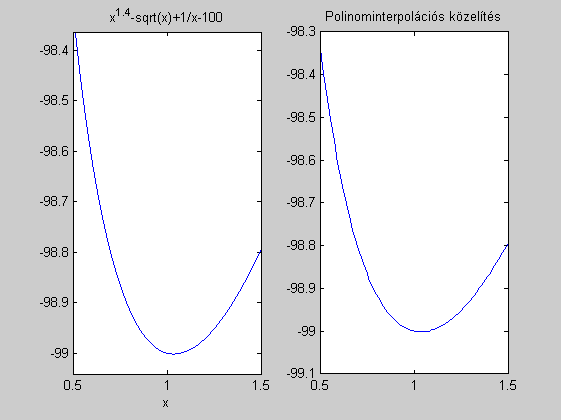
f=@(x)x.^(1.4)-sqrt(x)+1./x-100;
x=(0.5:0.2:1.5)';
disp('Adattáblázat')
format short
disp([x,f(x)])

z=polyfit(x,f(x),length(x)-1);
fv=polyval(z,1);
disp(['Polinominterpoláció hibája: ',num2str(abs(fv-f(1)))])

fv=interp1(x,f(x),1);
disp(['Szakaszonként lineáris interpoláció hibája: ',num2str(abs(fv-f(1)))])

fv=interp1(x,f(x),1,'spline');
disp(['Spline interpoláció hibája: ',num2str(abs(fv-f(1)))])

fv=interp1(x,f(x),1,'pchip');
disp(['Alakmegőrző interpoláció hibája: ',num2str(abs(fv-f(1)))])

subplot(1,2,1)
ezplot(f,[0.5,1.5])
subplot(1,2,2)
xx=0.5:0.01:1.5;
zz=polyval(z,xx);
plot(xx,zz)
title('Polinominterpolációs közelítés')

Adattáblázat
    0.5000  -98.3282
    0.7000  -98.8012
    0.9000  -98.9747
    1.1000  -98.9970
    1.3000  -98.9271
    1.5000  -98.7940
Polinominterpoláció hibája: 0.00034077
Szakaszonként lineáris interpoláció hibája: 0.014157
Spline interpoláció hibája: 0.00043395
Alakmegőrző interpoláció hibája: 0.0092252

4. feladat

x=[1,2,3,4]
y=[1,2,2,3]

format rat
polyfit(x,y,3)
disp('3x^3-(5/2)x^2+37/6x-3')
format short

x =
     1     2     3     4
y =
     1     2     2     3
ans =
       1/3           -5/2           37/6           -3       
3x^3-(5/2)x^2+37/6x-3

5. feladat

close all
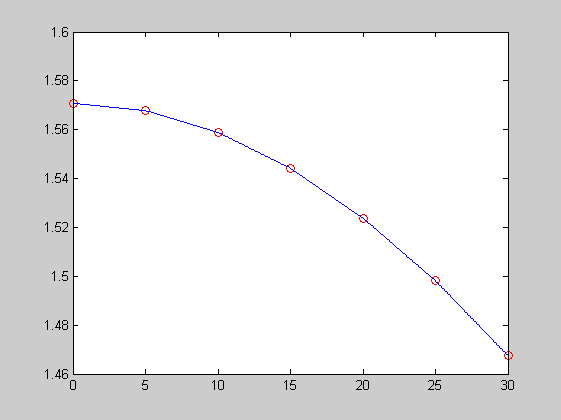
a=0:5:30;
I=[1.57079  1.56780 1.55888 1.54415 1.52379 1.49811 1.46746]

disp('I(18)')
interp1(a,I,18)

disp('I(22)')
interp1(a,I,22)

aa=0:0.1:30;
II=interp1(a,I,aa);
plot(a,I,'ro',aa,II,'b-')

I =
    1.5708    1.5678    1.5589    1.5441    1.5238    1.4981    1.4675
I(18)
ans =
    1.5319
I(22)
ans =
    1.5135

Published with MATLAB® 7.6