NUMERIKUS SZÁMÍTÁSOK 2. ÉVFOLYAMZH

Contents

KEDDI CSOPORT

A. csoport

1. feladat

%{
function [ertek,jel]=spint(v)
x=[0,1,2,3,4,5]; y=[2,4,5,3,2,1];
if v>=min(x) & v<=max(x)
    ertek=interp1(x,y,v,'spline');
    jel=1;
else
    ertek=interp1(x,y,(min(x)+max(x))/2,'spline');
    jel=0;
end
%}

2. feladat

f=@(x)[(x(1).^3.*sin(x(1))).^2+x(2).^2-3;x(1)-10*x(2)];
y=-2;
for x=-6:2:6
   mo=fsolve(f,[x,y]);
   fprintf('A (%2.0f,%2.0f) pontból indulva az (%9.6f,%9.6f) megoldást kapjuk.\n',x,y,mo(1),mo(2))
end

Optimization terminated: first-order optimality is less than options.TolFun.
A (-6,-2) pontból indulva az (-6.276657,-0.627666) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A (-4,-2) pontból indulva az (-3.193868,-0.319387) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A (-2,-2) pontból indulva az (-1.224643,-0.122464) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 0,-2) pontból indulva az (-1.224643,-0.122464) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 2,-2) pontból indulva az ( 1.224643, 0.122464) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 4,-2) pontból indulva az ( 3.193868, 0.319387) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 6,-2) pontból indulva az ( 6.276657, 0.627666) megoldást kapjuk.

3. feladat

f=@(x)x.*sin(x).^2;
b=2; %input('Adjuk meg az integrál felső határát (b>0)! ')
h=b/10;
x=0:h:b;
y=f(x);
Itrap=h*(y(1)/2+y(end)/2+sum(y(2:end-1)))
Imatlab=quad(f,0,b)

Itrap =
   1.582826106628502
Imatlab =
   1.585106701585246

4. feladat

f=@(t,y)[y(2);-0.083*y(2)^2];
[t,y]=ode45(f,[0,120],[0,6]);
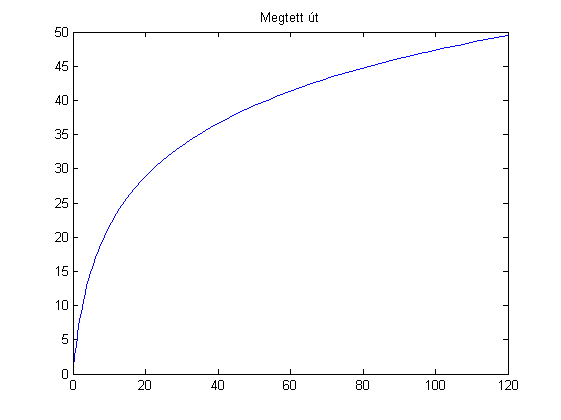
figure(1)
plot(t,y(:,1))
title('Megtett út')
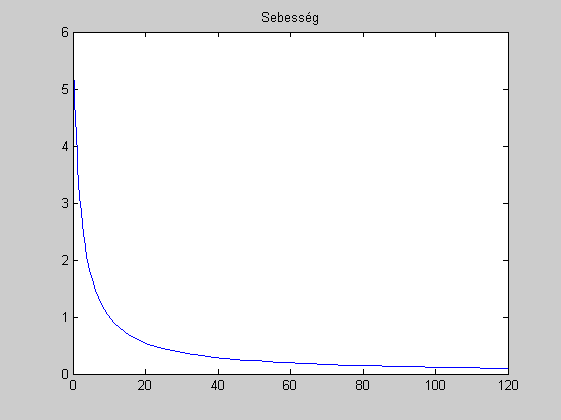
figure(2)
plot(t,y(:,2))
title('Sebesség')
disp('1 perc múlva a távolsága (méter)')
Hely_1perc=interp1(t,y(:,1),60)
sebesseg=@(ido)interp1(t,y(:,2),ido)-3;
disp('A fél sebesség elérésének ideje (másodperc)')
t_sebessegfel=fzero(sebesseg,20)
disp('Fél sebességnél a távolság (méter)')
Hely_sebfel=interp1(t,y(:,1),t_sebessegfel)

1 perc múlva a távolsága (méter)
Hely_1perc =
  41.347592024581594
A fél sebesség elérésének ideje (másodperc)
t_sebessegfel =
   2.014395178323106
Fél sebességnél a távolság (méter)
Hely_sebfel =
   8.361233064264264

B. csoport

1. feladat

%{
function [ertek,jel]=spint(s)
x=[0,2,4,6,8,10]; y=[2,4,5,3,2,1];
if s>=min(x) & s<=max(x)
    ertek=interp1(x,y,s,'pchip');
    jel=1;
else
    ertek=interp1(x,y,(min(x)+max(x))/2,'pchip');
    jel=0;
end
%}

2. feladat

f=@(x)[(x(1).^3.*sin(x(1))).^2+x(2).^2-3;x(1)-20*x(2)];
y=2;
for x=-6:2:6
   mo=fsolve(f,[x,y]);
   fprintf('A (%2.0f,%2.0f) pontból indulva az (%10.7f,%10.7f) megoldást kapjuk.\n',x,y,mo(1),mo(2))
end

Optimization terminated: first-order optimality is less than options.TolFun.
A (-6, 2) pontból indulva az (-6.2762955,-0.3138148) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A (-4, 2) pontból indulva az (-3.1945214,-0.1597261) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A (-2, 2) pontból indulva az (-1.2253119,-0.0612656) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 0, 2) pontból indulva az ( 1.2253119, 0.0612656) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 2, 2) pontból indulva az ( 1.2253119, 0.0612656) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 4, 2) pontból indulva az ( 3.1945214, 0.1597261) megoldást kapjuk.
Optimization terminated: first-order optimality is less than options.TolFun.
A ( 6, 2) pontból indulva az ( 6.2762955, 0.3138148) megoldást kapjuk.

3. feladat

f=@(x)x.*cos(x).^2;
b=2; %input('Adjuk meg az integrál felső határát (b>0)! ')
h=b/20;
x=0:h:b;
y=f(x);
Itrap=h*(y(1)/2+y(end)/2+sum(y(2:end-1)))
Imatlab=quad(f,0,b)

Itrap =
   0.415465080521440
Imatlab =
   0.414893298414754

4. feladat

f=@(t,y)[y(2);-0.073*y(2)^2];
[t,y]=ode45(f,[0,180],[0,15]);
figure(1)
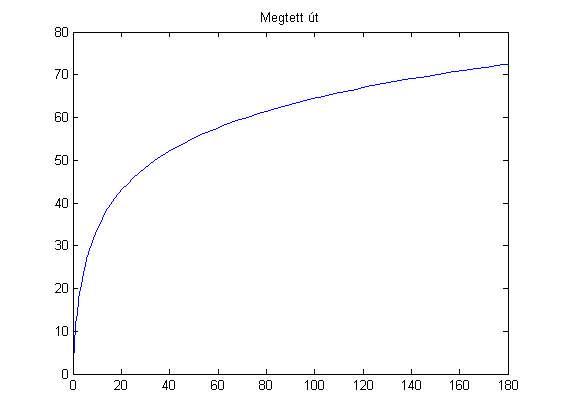
plot(t,y(:,1))
title('Megtett út')
figure(2)
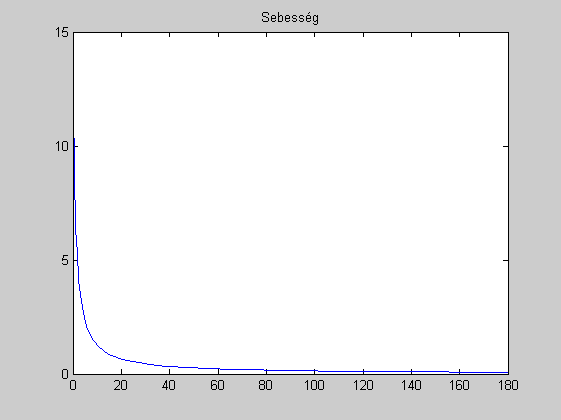
plot(t,y(:,2))
title('Sebesség')
disp('2 perc múlva a távolsága (méter)')
Hely_2perc=interp1(t,y(:,1),120)
sebesseg=@(ido)interp1(t,y(:,2),ido)-1.5;
disp('A tized sebesség elérésének ideje (másodperc)')
t_sebessegtized=fzero(sebesseg,40)
disp('A tized sebességnél a távolság (méter)')
Hely_sebtized=interp1(t,y(:,1),t_sebessegtized)

2 perc múlva a távolsága (méter)
Hely_2perc =
  66.972372684053184
A tized sebesség elérésének ideje (másodperc)
t_sebessegtized =
   8.232645714275407
A tized sebességnél a távolság (méter)
Hely_sebtized =
  31.569651399126201

Csütörtöki csoport

A. csoport

1. feladat

%{
function [I,modszer]=elso(f,a,b)
if b-a<10
   h=(b-a)/20;
   x=a:h/2:b;
   y=f(x);
   I=h/6*(y(1)+y(end)+4*sum(y(2:2:end-1))+2*sum(y(3:2:end-2)));
   modszer=0;
else
    I=quad(f,a,b);
    modszer=1;
end;
%}

2. feladat

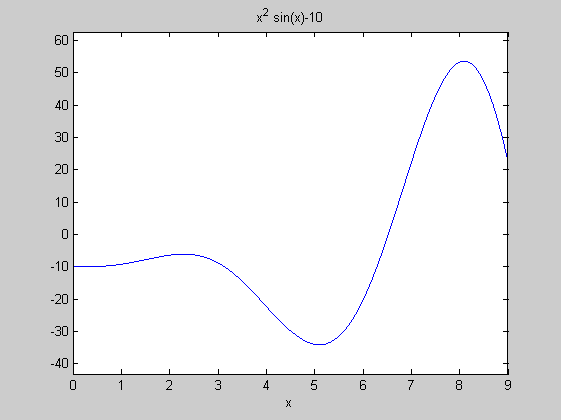
f=@(x)x.^2.*sin(x)-10;
ezplot(f,[0,9])
fd=@(x)2*x*sin(x)+x.^2.*cos(x)
fprintf('Kezdőérték    Matlab        Newton\n');
for x=1:8
    xM=fzero(f,x);
    xN=x;
    for i=1:30
        xN=xN-f(xN)/fd(xN);
    end
    fprintf('%1f      %10.8f     %10.8f\n',x,xM,xN);
end

fd = 
    @(x)2*x*sin(x)+x.^2.*cos(x)
Kezdőérték    Matlab        Newton
1.000000      -3.87184599     40.83470736
2.000000      6.52060253     12.62910989
3.000000      6.52060253     6.52060253
4.000000      6.52060253     6.52060253
5.000000      6.52060253     -9.53499250
6.000000      6.52060253     6.52060253
7.000000      6.52060253     6.52060253
8.000000      6.52060253     103.67162715

3. feladat

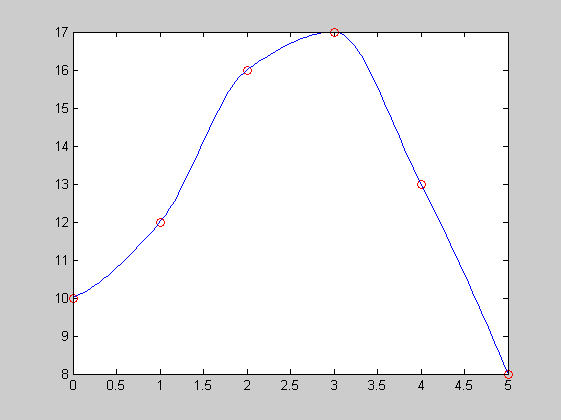
t=[0,1,2,3,4,5]
T=[10,12,16,17,13,8]

% ido=input('Időpont 0 és 5 között:')
ido=3.5
Kozelito_homerseklet=interp1(t,T,ido,'pchip')
xx=linspace(0,5,100);
yy=interp1(t,T,xx,'pchip');
plot(t,T,'ro',xx,yy,'b-')

t =
     0     1     2     3     4     5
T =
    10    12    16    17    13     8
ido =
   3.500000000000000
Kozelito_homerseklet =
  15.555555555555555

4. feladat

a=0.002; r=1.05;
f=@(t,y)[-a*y(1).*y(2);a*y(1).*y(2)-r*y(2)];
[t,y]=ode45(f,[0,4],[10000,1]);
figure(1)
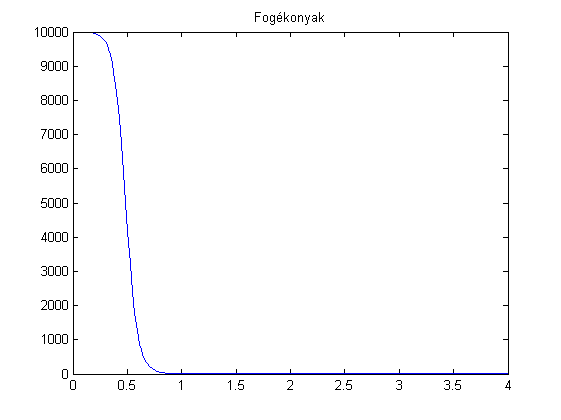
plot(t,y(:,1))
title('Fogékonyak')
figure(2)
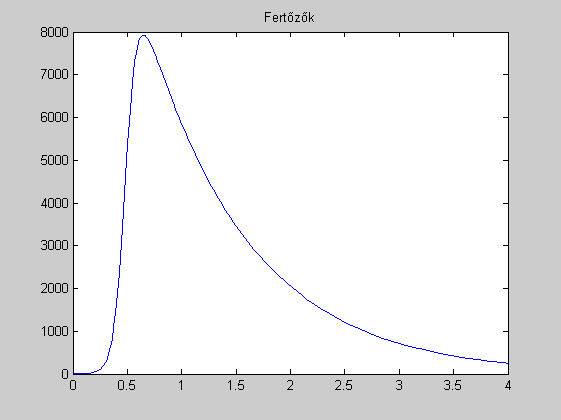
plot(t,y(:,2))
title('Fertőzők')
[Max_fertozoszam,p]=max(y(:,2));
Max_fertozoszam
Max_fertozes_ideje=t(p)
fertozo=@(ido)interp1(t,y(:,2),ido)-1000;
t_1000=fzero(fertozo,0.5);
Egeszseges_1000fertozo=interp1(t,y(:,1),t_1000)

Max_fertozoszam =
    7.927416783988494e+003
Max_fertozes_ideje =
   0.652746194559316
Egeszseges_1000fertozo =
    8.942236600553270e+003

B. csoport

1. feladat

%{
function [I,modszer]=elso(f,a,b)
if b-a<5
   h=(b-a)/10;
   x=a:h/2:b;
   y=f(x);

   I=h/6*(y(1)+y(end)+4*sum(y(2:2:end-1))+2*sum(y(3:2:end-2)));
   modszer=1;
else
    I=quad(f,a,b);
    modszer=0;
end;
%}

2. feladat

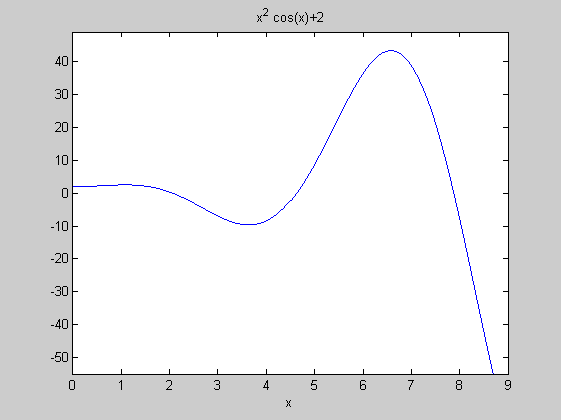
f=@(x)x.^2.*cos(x)+2;
ezplot(f,[0,9])
fd=@(x)2*x*cos(x)-x.^2.*sin(x)
fprintf('Kezdőérték    Newton        Matlab\n');
for x=5:12
    xM=fzero(f,x);
    xN=x;
    for i=1:30
        xN=xN-f(xN)/fd(xN);
    end
    fprintf('%1f      %11.8f     %11.8f\n',x,xN,xM);
end

fd = 
    @(x)2*x*cos(x)-x.^2.*sin(x)
Kezdőérték    Newton        Matlab
5.000000       4.61848831      4.61848831
6.000000       4.61848831      4.61848831
7.000000       7.88614602      7.88614602
8.000000       7.88614602      7.88614602
9.000000       7.88614602      7.88614602
10.000000      10.97898125     10.97898125
11.000000      10.97898125     10.97898125
12.000000      10.97898125     10.97898125

3. feladat

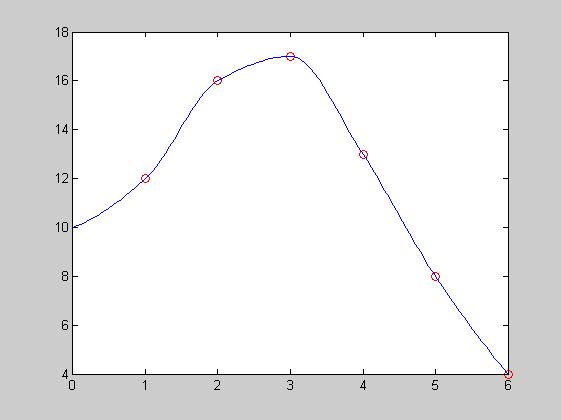
t=[0,1,2,3,4,5,6]
T=[10,12,16,17,13,8,4]

%ido=input('Időpont 0 és 6 között:')
ido=3.5;
Kozelito_homerseklet=interp1(t,T,ido,'pchip')
xx=linspace(0,6,100);
yy=interp1(t,T,xx,'pchip');
plot(t,T,'ro',xx,yy,'b-')

t =
     0     1     2     3     4     5     6
T =
    10    12    16    17    13     8     4
Kozelito_homerseklet =
  15.555555555555555

4. feladat

a=0.01; r=1.1;
f=@(t,y)[-a*y(1).*y(2);a*y(1).*y(2)-r*y(2)];
[t,y]=ode45(f,[0,6],[1000,1]);
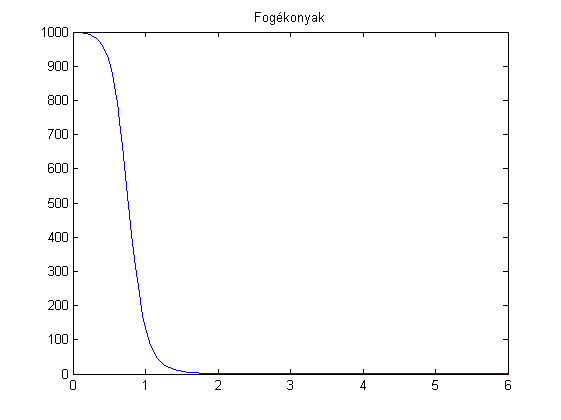
figure(1)
plot(t,y(:,1))
title('Fogékonyak')
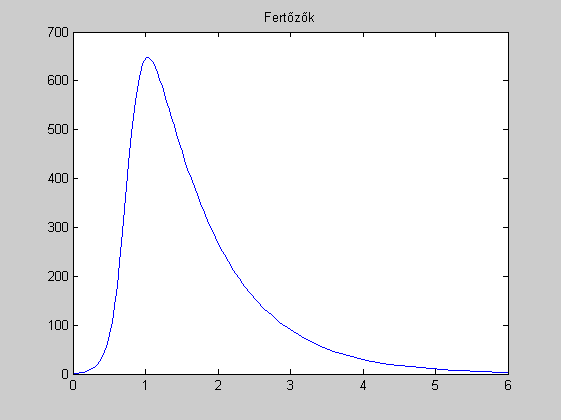
figure(2)
plot(t,y(:,2))
title('Fertőzők')
[Max_fertozoszam,p]=max(y(:,2));
Max_fertozoszam
Max_fertozes_ideje=t(p)
fertozo=@(ido)interp1(t,y(:,2),ido)-100;
t_100=fzero(fertozo,0.5);
Egeszseges_100fertozo=interp1(t,y(:,1),t_100)

Max_fertozoszam =
    6.480025694222253e+002
Max_fertozes_ideje =
   1.042219175114514
Egeszseges_100fertozo =
    8.879092572431989e+002

Published with MATLAB® 7.6