Hatodik labor: Gyakorló óra
1. feladat: Írjunk egy olyan szorzoTabla(n,m) nevű függvényt, melynek bemenete n és m pozitív egészek, és a kimenete egy mátrix, melynek elemei a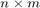 
-es szorzótábla értékei.
2. feladat: Írjunk egy olyan fibonacciSzorzat(n) nevű függvényt, melynek bemenete n pozitív egész, és a kimenete a Fibonacci-sorozat n-edik és n+1-edik tagjának szorzata. (A Fibonacci sorozat elsõ és második tagja 1, és minden elem az õt megelőző két elem összege.)
3. feladat: Írjunk egy olyan idenJanuar(n) nevű függvényt, melynek bemenete n egy és 31 közötti pozitív egész, és kiírja, hogy idén január n-edike milyen napra esett.
4. feladat: Írjunk olyan idosebb(ev1, ho1, nap1, ev2, ho2, nap2) nevű függvényt, melynek bemenete 6 pozitív valós szám, melyek két ember születésnapját jelentik. A kimenet legyen 0, ha egyidősek, 1 ha az első ember idõősebb, 2, hogy ha a második.
5. feladat: Írjunk egy olyan hanyadikelem(v,n) nevű függvényt melynek elsõ bemenete egy számokból álló sorvektor, a második egy valós szám. A függvény határozza meg, hogy hányadik helyen szerepel elõször v-ben n, a kimenet legyen ezen index. Ha nem szerepel n a vektorban, akkor a kimenet legyen -1.
6. feladat: Írjunk egy olyan csere(v,a,b) nevû függvényt, melynek 3 bemenete van: egy v vektor, és két valós szám: a és b. A függvény cserélje ki v minden a-val egyenlõ elemét b-re.
7. feladat: Írjunk egy olyan szamolAtlag(v) nevû függvényt, amelynek bemenete egy sorvektor, amelyben valós számok vannak. A függvény kimenete legyen a v vektor 0 és -1 közé eső elemeinek összege.
8. feladat: Írjunk olyan mennyiDb(v) nevű függvényt amely meghatározza a bemenetként kapott v vektor páratlan indexű helyein lévõ egész elemeinek számát.