Harmadik labor
Contents
Ciklusszervezés
for ciklus
for futó index= vektor parancsblokk end
Vektorok létrehozására kifejezetten lassú
tic %stopert indít for i=1:1e7 nemtuljo(i)=i; end toc %megmondja mennyi ideig futott
Elapsed time is 1.911445 seconds.
Voltaképpen a legtöbb időt azzal veszítettük, hogy minden iterációban törölnie kellett a régi nemjo valtozó értékét, mert megváltoztattuk a méretét. Ezen a problémán preallokációval segíthetünk, ha előre tudjuk a méretet.
tic kozepes=zeros(1,1e7); for i=1:1e7 kozepes(i)=i; end toc
Elapsed time is 0.105547 seconds.
Viszont a legjobb megoldás
tic jobb=1:1e7; toc
Elapsed time is 0.066837 seconds.
ezért használjuk a múlt órán megismert : operátort amikor csak lehet
Valójában a for ciklus változója sem kötelező, hogy számok számtani sorozata legyen, lehet bármilyen előre definiált vektor.
v=[ 1 6 2 9 4 6]; for i=v fprintf('Az i változó értéke:%d\n',i) end
Az i változó értéke:1 Az i változó értéke:6 Az i változó értéke:2 Az i változó értéke:9 Az i változó értéke:4 Az i változó értéke:6
while ciklus while feltétel igaz parancsblokk end
i=0;% nincs saját futó indexe, ha szükség van rá nekünk kell létrehozni while i<10 i=i+1; end % CTRL+C hatására megszakítja a számítást
Viszont a for ciklus nagyon meglepően viselkedik:
for i=1:3 fprintf('Az i változó értéke:%d\n',i) i=3; fprintf('Az i változó értéke:%d\n',i) end
Az i változó értéke:1 Az i változó értéke:3 Az i változó értéke:2 Az i változó értéke:3 Az i változó értéke:3 Az i változó értéke:3
A ciklusváltozó értéke ugyan megváltoztatható a ciklus belsejében, de a következő iterációra ez nincsen hatással!
Például ennek segítségével megkereshetjük az első 0 elem pozícióját egy vektorban
v=[1 4 2 8 5 79 8]; i=1; while i<=length(v) && v(i)~=0 i=i+1; end if i<=length(v) fprintf('Az első 0 pozíciója: %d \n', i) else fprintf('Nincs a vektorban 0 elem\n') end
Nincs a vektorban 0 elem
Break, continue, return és error használata
a break hatására megszakítja a ciklust, így az előbbi programunk:
v=[1 3 2 5 8 0 5 2 7]; i=1; while v(i)~=0 i=i+1; if i>length(v) break end end if i<=length(v) fprintf('Az elsõ 0 poziciója: %d \n', i) else fprintf('Nincs a vektorban 0 elem\n') end
Az elsõ 0 poziciója: 6
A continue hatására átugorja a hátralévő parancsokat, és a következő iterációval folytatja. Mind a break, mind a continue csak a belső ciklusból ugrik ki egymásba ágyazott ciklusok esetén.
A return parancsot nem csak ciklus belsejében adhatjuk ki, hanem egy függvényen belül bárhol. Hatására a Matlab megszakítja a függvény futását és kilép. Amennyiben addig kapott értéket a kimenet, akkor a függvény azzal visszatér.
A bemeneteket ellenőrizve az error parancs segítségével megállíthatjuk a függvény futását és kilépünk belőle. Ekkor a függvény egyetlen kimenet értékét sem adja vissza, akkor sem, ha más definiáltuk.
Tippeljük meg az alábbi függvény kimenetét az alábbi bemenetekkel meghívva: 1.5, 7, 2.5, -1.5.
function ki=furapelda(be) ki=0; if be<0 error('Negatív számmal hívtad meg') end if be>2 ki=2; end return ki=3;
Lebegőpontos számítások furcsaságai
Túlcsordulás
A Matlab dupla pontosságú lebegőpontos ábrázolásában 52 bit jut a mantisszára (értékes jegyek száma), 1 előjelbit, 11 jegy a karakterisztikára (de ebből egy előjelbit). Ennek következménye:
(2^53+1)-2^53
ans =
0
A legkisebb ábrázolható szám: 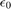
realmin
ans = 2.2251e-308
Viszont ez nem azt jelenti, hogy ilyen finomsággal tudjuk ábrázolni a lebegőpontos számokat. Ezt az 1 utáni legkisebb ábrázolható szám adja meg: 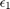
format long
1+2^-52==1
ans = logical 0
1+2^-53==1
ans = logical 1
Ez nagyjából 15 értékes jegynek felel meg, ennyi a maximális szóba jövő számítási pontosság. Sajnos ez sem mindig elérhető.
Összeadás
s=1; p=0; for i=1:10 s=s+10^(-16); p=p+10^(-16); end s
s =
1
p=p+1
p = 1.000000000000001
Azaz érdemes először a kicsi tagokat összeadni, nem mindegy a sorrend.
Kivonás
Vegyük a két elvben egyforma mennyiséget: sqrt(a)-sqrt(a-1), illetve 1/(sqrt(a)+sqrt(a-1)).
c=sqrt(10^6)-sqrt(999999)
c =
5.000001250436981e-04
d=1/(sqrt(10^6)+sqrt(999999))
d =
5.000001250000625e-04
Kiegyszerűsödés: két közeli szám kivonásakor fellépő jegyveszteség Ha a két számban az első k jegy azonos, akkor a különbségükben az első k jegy értéktelen Az elsőben az utolsó 6 jegy nem stimmel, a második a jó. Tanulság: numerikusan megbízhatatlan egymáshoz közeli számok kivonása.
Órai feladatok
1. feladat: Írjunk olyan függvényt, amelynek bemenete egy A mátrix, és kimenetként listázza azon elemek pozícióját amely nagyobbak, mint a két indexük összege.
2.feladat: Írjunk olyan függvényt, amely egy bemenetként kapott v vektor első 6-nál nagyobb elemének pozicióját adja kimenetként. Ha nincs ilyen elem, akkor a kimenet értéke legyen -1.
3. feladat: Írjunk egy olyan függvényt, melynek bemenete egy v vektor. A kimenet legyen egy olyan vektor, melyben v elemei helyett 0-k szerepelnek addig, amíg el nem érünk az első 100-nál nagyobb elemhez v-ben. Onnan pedig v elemei legyen benne változtatás nélkül.
4. feladat: Írjunk olyan reciprokOsszeg(n) nevű függvényt, amelynek kimenete a legkisebb olyan k pozitív egész, melyre az 1 + 1/2 + 1/3 + · · · + 1/k összeg nagyobb, mint a bemenetként kapott pozitív n szám. Ha 10^5 -nél is több tag kellene, akkor a kimenet legyen −1.
5. feladat: Készítsünk egy olyan függvényt, amely minél pontosabban oldja meg a másodfokú egyenletet (vizsgálja, hogy lehet-e kiegyszerűsödés a megoldóképletben). A függvény három bemenete legyen az ax^2+bx+c=0 egyenletből az a, b, és c együtthatók, a kimenet legyen a két gyök.
6. feladat: Írjunk egy olyan függvényt, amelynek bemenete egy pozitív egész szám (mondjuk n). A függvény számítsa ki minél pontosabban az alábbi sorösszeg első n tagjának felhasználásával ln(1.5) értékét 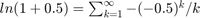 .
.