Órai feladatok

1. feladat: Írjunk olyan függvényt, amelynek bemenete egy A mátrix, és kimenetként listázza azon elemek pozícióját amely nagyobbak, mint a két indexük összege.

function ki=nagyElem(bematrix)
ki=[];
for i=1:size(bematrix,1)
    for j=1:size(bematrix,2)
        if bematrix(i,j)>i+j
            ki=[ki; i j];
        end
    end
end

2.feladat: Írjunk olyan függvényt, amely egy bemenetként kapott v vektor első 6-nál nagyobb elemének pozicióját adja kimenetként. Ha nincs ilyen elem, akkor a kimenet értéke legyen -1.

function ki=nagye(v)

ki=-1;
i=1;

while i<=length(v)
    if v(i)>6 
        ki=i; 
        return 
    end
    
    i=i+1;
end

3. feladat: Írjunk egy olyan függvényt, melynek bemenete egy v vektor. A kimenet legyen egy olyan vektor, melyben v elemei helyett 0-k szerepelnek addig, amíg el nem érünk az első 100-nál nagyobb elemhez v-ben. Onnan pedig v elemei legyen benne változtatás nélkül.

function ki=nullaz(v)
ki=v;
k=1;
while k<=length(v)
   if v(k)>100
       break
   end
   ki(k)=0;
   k=k+1;
end

4. feladat: Írjunk olyan reciprokOsszeg(n) nevű függvényt, amelynek kimenete a legkisebb olyan k pozitív egész, melyre az 1 + 1/2 + 1/3 + · · · + 1/k összeg nagyobb, mint a bemenetként kapott pozitív n szám. Ha 10^5 -nél is több tag kellene, akkor a kimenet legyen −1.

function ki=reciprokOsszeg(n)

osszeg=0;

for i=1:1e5
    osszeg=osszeg+1/i;
    if osszeg>n 
        ki=i; 
        return
    end
end
ki=-1;

5. feladat: Készítsünk egy olyan függvényt, amely minél pontosabban oldja meg a másodfokú egyenletet (vizsgálja, hogy lehet-e kiegyszerűsödés a megoldóképletben). A függvény három bemenete legyen az ax^2+bx+c=0 egyenletből az a, b, és c együtthatók, a kimenet legyen a két gyök.

function [gyok1, gyok2]=masodfoku(a,b,c)
% Thf nem hiányos, azaz a~=0
if a==0
    error('A kapott másodfokú egyenlet hiányos')
end

D=sqrt(b^2-4*a*c);

if b>0
    gyok1=-2*c/(b+D);
    gyok2=(-b-D)/(2*a);
elseif b<0
    gyok1=(-b+D)/(2*a);
    gyok2=(-2*c)/(b-D);
else
    gyok1=(+D)/(2*a);  
    gyok2=(-D)/(2*a);    
end

6. feladat: Írjunk egy olyan függvényt, amelynek bemenete egy pozitív egész szám (mondjuk n). A függvény számítsa ki minél pontosabban az alábbi sorösszeg első n tagjának felhasználásával ln(1.5) értékét 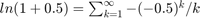$ln(1+0.5)=\sum_{k=1}^{\infty} -(-0.5)^k/k$ .

function kbln=sorLn(n)

kbln=0;
for i=n:-1:1
    kbln=kbln-(-0.5)^i/i;
end