Negyedik labor: Adatok importálása és megjelenítése

Contents

Számokat tartalmazó .csv formátumú fájlok (az egyes értékek sorokon belül vesszővel vannak elválasztva, sorok végén új sor karakter) a dlmread parancs segítségével olvasható be. A fájlnak vagy ugyanabban a könyvtárban kell lennie, vagy meg kell adnunk a helyét. Pl:

ad=dlmread('adatok.csv');

Ez egy olyan fájl, amiben 20000 ember adatai vannak. Oszloponként: magasság cm-ben, testsúly kg-ban, kor évben .

Hisztogram készítése

Egy hisztogramon ábrázolhatjuk például a magasság eloszlását.

ladak=histogram(ad(:,1))

ladak = 

  Histogram with properties:

             Data: [20000×1 double]
           Values: [1×41 double]
          NumBins: 41
         BinEdges: [1×42 double]
         BinWidth: 2
        BinLimits: [140 222]
    Normalization: 'count'
        FaceColor: 'auto'
        EdgeColor: [0 0 0]

  Use GET to show all properties

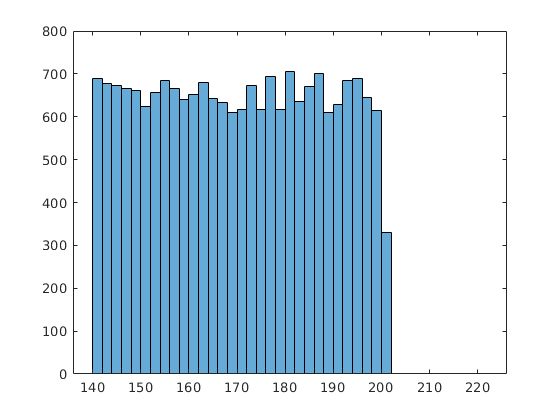
Egy kimenettel meghívva egy struct típusú változót kapunk. A struct típusú változókban egyszerre tárolhatunk többféle típusú adatot. Akárhány mezője lehet a változónak (itt a ladak változónak), de egy mezőben egyféle adat található. Itt például a BinEdges nevű mezőben vannak a szakaszok határai, a NumBins mező mondja meg, hogy hány intervallumot hozott létre, a Values mező, hogy egy intervallumba hány elem esik. Ha a mező konkrét értékére van szükségünk, akkor az a pont segítségével érhetjük el, például:

ladak.Values

ans =

  Columns 1 through 13

   690   677   674   667   662   623   657   684   665   640   653   679   642

  Columns 14 through 26

   634   609   617   673   618   695   618   706   635   670   702   610   629

  Columns 27 through 39

   685   689   646   615   331     1     0     1     0     0     0     1     0

  Columns 40 through 41

     0     2

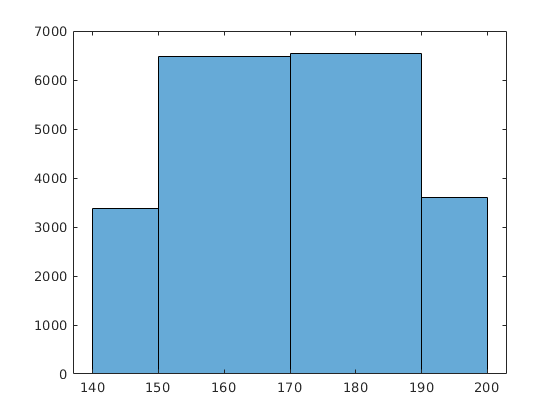
Amennyiben szükségünk van rá, megváltoztathatjuk a szakaszok beosztását, például megadhatjuk az intervallumok határait, így gyorsan megtudhatjuk az egyes intervallumokba eső adatok számát.

ladak2=histogram(ad(:,1),[140,150,170,190,200])

ladak2 = 

  Histogram with properties:

             Data: [20000×1 double]
           Values: [3370 6486 6544 3595]
          NumBins: 4
         BinEdges: [140 150 170 190 200]
         BinWidth: 'nonuniform'
        BinLimits: [140 200]
    Normalization: 'count'
        FaceColor: 'auto'
        EdgeColor: [0 0 0]

  Use GET to show all properties

Boxplot

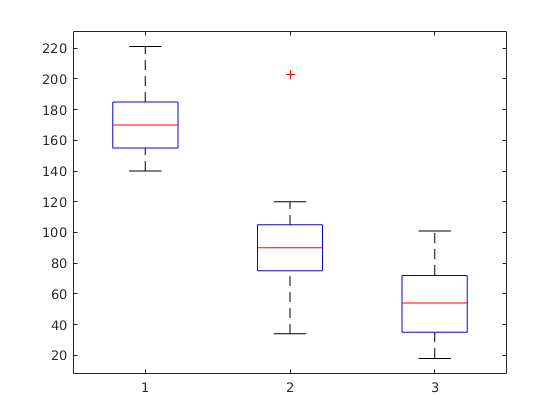
A változónk terjedelmét, illetve mediánját a boxplot paranccsal jeleníthetjük meg. A box alja és teteje a 25%-os ill. 75%-os percentilis, de ábrázolja a szélsőséges értékeket is piros kereszttel.

boxplot(ad)

Függvények ábrázolása

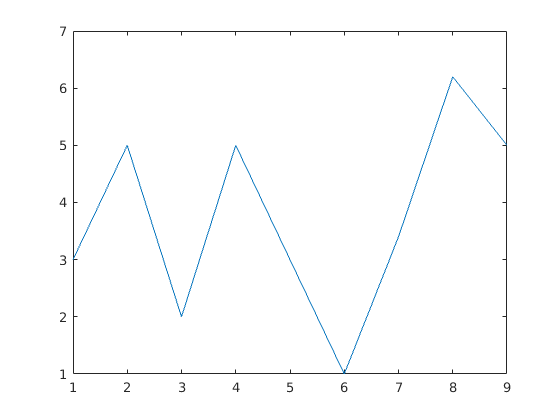
ha csak egy vektor elemeit akarom ábrázolni

v=[3 5 2 5 3 1 3.4 6.2 5];
plot(v)

Adhatunk stílusparancsokat is

plot(v,'ro')

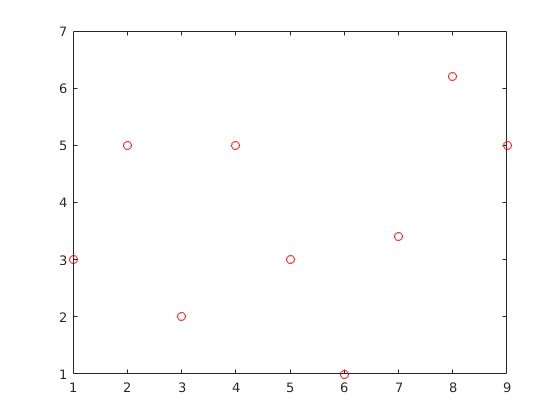
Ha egy egy függvényt, akkor először létrehozok egy sorvektort, ez lesz az x tengelyen:

t=linspace(0,2*pi,100);
plot(t,sin(t),'r');

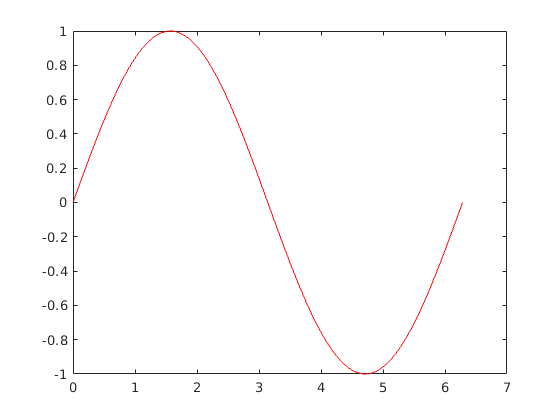
Vigyázat, bár az alábbi megoldás sem ad errort, mégis félrevezető (tengelyek!)

plot(sin(t));

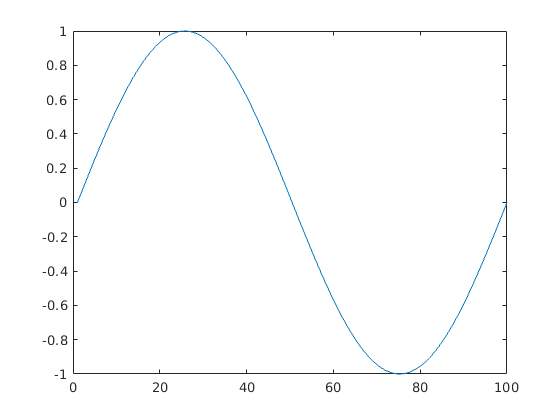
Több függvény egy ábrán

Lehet több vektor is egy plot belsejében, csak páronként kell egyforma hosszúaknak lenniük

plot(0,0,'r+',sin(t),cos(t));

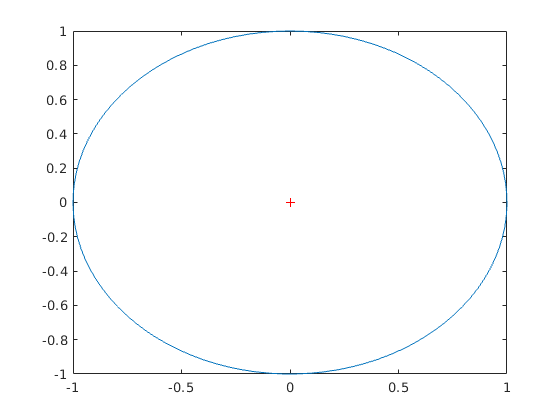
vagy: hold on parancs, akkor több különböző plot-ot is egy ábrára rak, például:

plot(v,'ro')
hold on
plot(t,sin(t))

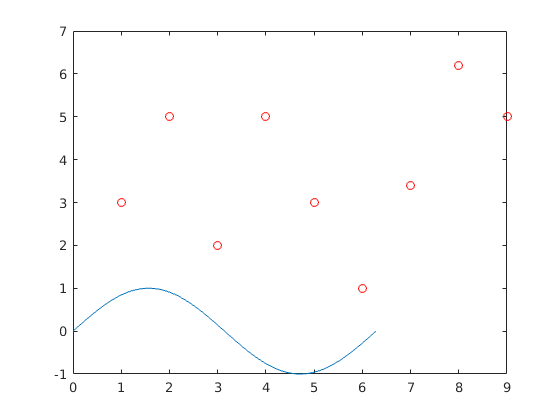
látjuk, hogy a tengelyt igazítja a legnagyobb értékekhez

hold off % ez kapcsolja ki

Paraméteres görbe kirajzolása

Ekkor nem egy függvényt ábrázolunk, hanem külön megadjuk az x és y koordinátákat.

x=linspace(0,2*pi);
plot(cos(x),sin(x))

text(cos(x(1)),sin((x(1))), 'Kezdőpont');
xlabel('x tengely')
ylabel('y tengely')
title('Ez egy kör')
axis('equal','square')
grid on;

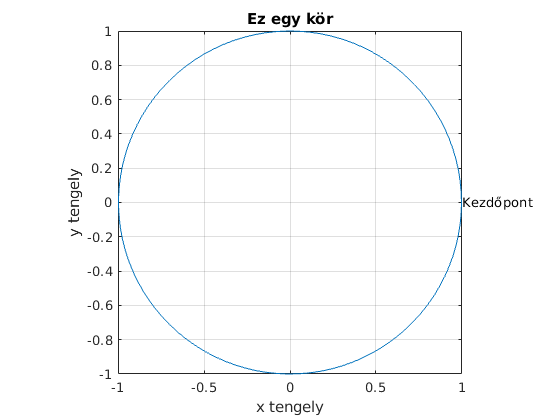
Több kép egy ábrán

t=-4:0.1:4;
subplot(2,1,1);
plot(t,sin(t))
title('A sin függvény');
subplot(2,2,3);
plot(t,cos(t))
title('A cos függvény');
subplot(2,2,4);
plot(t,exp(t))
title('Az exponenciális függvény');

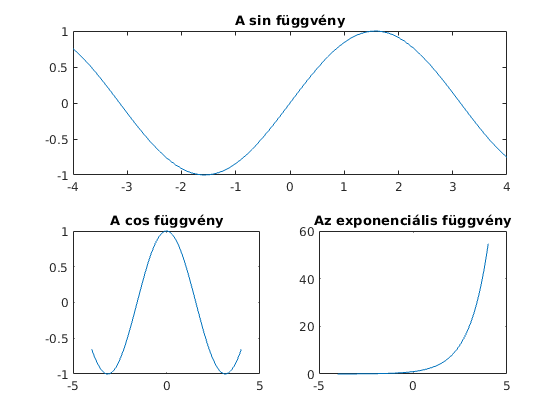
Képek exportálása

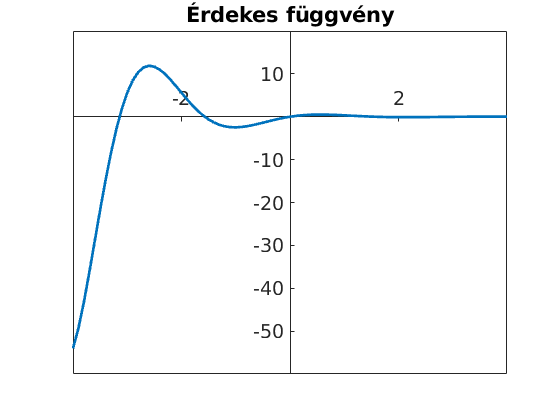
Betűméretre ügyeljünk, az alap fontméret nem fog látszani az importált képen, célszerű a vonalszélességet is átállítani. A már megismert struct segítségével további beállításokat is elérhetünk, az alábbi példában a betűméreten kívül azt állítottuk be, hogy a tengelyek az origóban metsszék egymást.

figure
plot(t,sin(2*t)./exp(t),'LineWidth',2)
title('Érdekes függvény')
ax=gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
set(gca,'fontsize',14)

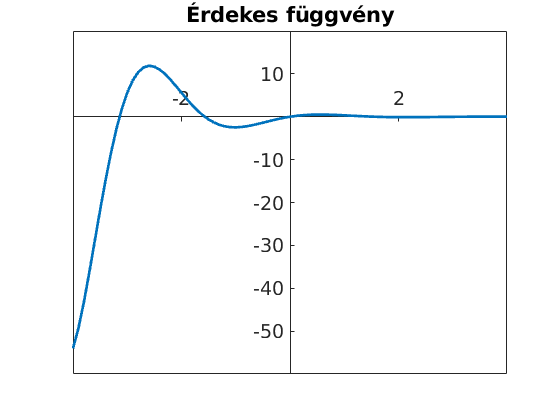
A saveas parancs végzi a tényleges mentést. Többféle formátum is lehetséges: pdf, jpg, eps, ...

saveas(gca, 'abra.jpg')

Térbeli ábrák kirajzolása

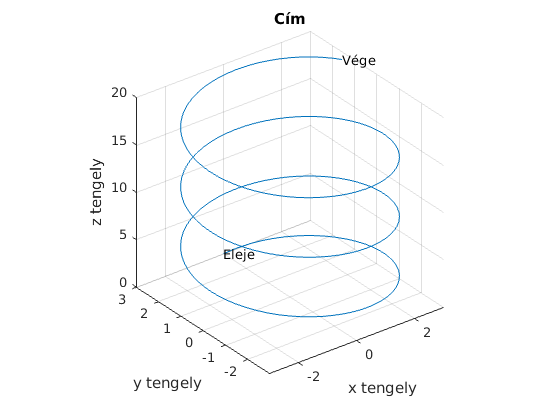
A plot3 paranccsal térbeli vonalat rajzolhatunk ki:

x=0:0.1:20;
plot3(3*sin(x),3*cos(x),x)
text(3*sin(x(1)),3*cos(x(1)),x(1), 'Eleje');
text(3*sin(x(201)), 3*cos(x(201)),x(201),'Vége');
xlabel('x tengely'), ylabel('y tengely'), zlabel('z tengely')
title('Cím')
axis('equal','square')
grid on;

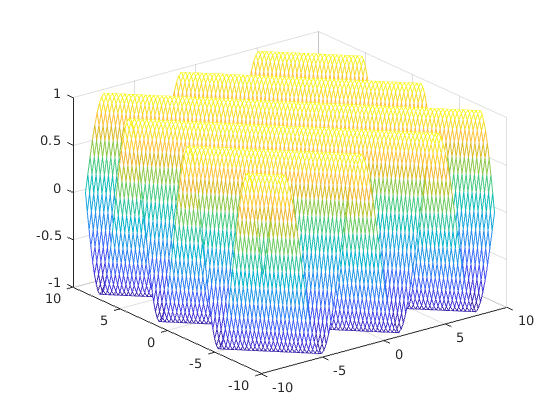
Míg felületek ábrázolására a mesh parancs szolgál. Először egy rácsot kell definiálnunk, ami felett ábrázolunk. Az x és y tengely beosztása:

x=linspace(-3*pi,3*pi);
y=x;

A meshgrid parancs hozza létre magát a rácsot:

[xx,yy]=meshgrid(x,y);

Végül kiszámoljuk az ábrázolandó függvényértékeket ezen rács felett:

z=sin(xx+yy);

És végül a mesh parancs segítségével ábrázoljuk:

mesh(x,y,z)

Órai feladatok

A kérések megválaszolásánál igyekezzünk elkerülni a ciklusok használatát!

1. feladat: Ábrázoljuk az emberek testtömegindexének (súly kg-ban osztva magasság négyzetével m-ben) eloszlását az adatok.csv fájl alapján. Derítsük ki, hogy

2. feladat: Válaszoljuk meg az előbbi kérdéseket külön-külön a 30 év alatti és a 45 év feletti emberekre is.

3. feladat: Próbáljuk ki, mit történik, ha az A=[3 4 2 3; 1 3 5 1; -9 5 2 5] mátrixot ábrázoljuk, azaz kiadjuk a plot(A) parancsot. Keressünk magyarázatot a látottakra.

4. feladat: Ábrázoljuk az x(t)=t*cost(t), y(t)=t*sin(t) paraméteres görbét a síkon, a t paraméter értéke menjen 0 és 10 között. Lássuk el az ábrát feliratokkal, majd mentsük egy .jpg fájlba.

5. feladat: Írjunk egy olyan fvElojel(a,b,f) nevű függvényt, melynek első két bemenete egy-egy valós szám, amelyek egy intervallum két végpontját jelentik (és a<b), a harmadik bemenete pedig egy függvény. A fvElojel(a,b,f) ábrázolja az f függvényt az [a,b] intervallumon, valamint írja ki a képernyőre, hogy a két végpontban eltérő-e a függvényértékek előjele. A függvények ne legyen kimenete.

6. feladat: Rajzoljunk egy 1 sugarú felső félgömböt.

Published with MATLAB® R2018b