Hatodik labor: Gyakorló óra
1. feladat: Írjunk egy olyan szorzoTabla(n,m) nevű függvényt, melynek bemenete n és m pozitív egészek, és a kimenete egy mátrix, melynek elemei a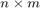 
-es szorzótábla értékei.
2. feladat: Írjunk egy olyan fibonacciSzorzat(n) nevű függvényt, melynek bemenete n pozitív egész, és a kimenete a Fibonacci-sorozat n-edik és n+1-edik tagjának szorzata. (A Fibonacci sorozat első és második tagja 1, és minden elem az azt megelőző két elem összege.)
3. feladat: Írjunk egy olyan idenJanuar(n) nevű függvényt, melynek bemenete n egy és 31 közötti pozitív egész, és kiírja, hogy idén január n-edike milyen napra esett.
4. feladat: Írjunk olyan idosebb(ev1, ho1, nap1, ev2, ho2, nap2) nevű függvényt, melynek bemenete 6 pozitív valós szám, melyek két ember születésnapját jelentik. A kimenet legyen 0, ha egyidősek, 1 ha az első ember idősebb, 2, hogy ha a második.
5. feladat: Írjunk egy olyan csere(v,a,b) nevű függvényt, melynek 3 bemenete van: egy v vektor, és két valós szám: a és b. A függvény cserélje ki v minden a-val egyenlő elemét b-re.
6. feladat: Írjunk egy olyan szamolAtlag(v) nevű függvényt, amelynek bemenete egy sorvektor, amelyben valós számok vannak. A függvény kimenete legyen a v vektor 0 és -1 közé eső elemeinek átlaga.
7. feladat: Írjunk egy elliP(a,b) nevű függvényt, amelynek két bemenete egy-egy pozitív valós szám. A függvény rajzolja ki a x(t)=a*cos(t), y(t)=b*sin(t) paraméteres görbét, ahol a t paraméter 0 és 2*pi között megy, majd mentse el a címmel és tengelyfeliratokkal ellátott ábrát egy jpg-fájlba. A függvénynek ne legyen kimenete.
8. feladat: Írjon egy histMod(v,a,b) nevű függvényt, amely v bemenete egy sorvektor, a és b valós számok. A függvény dobja el v minden olyan elemét, amelynek értéke kevesebb mint a vagy több mint b, majd ábrázolja a megmaradt elemek eloszlását hisztogramon.
9. feladat: Adott egy xls fájl, melynek első oszlopában nevek vannak, a másodikban a születési dátumok éééé.hh.nn formátumban. Írjunk egy celKoz(s) nevű függvényt, melynek bemenete a fájl teljes neve sztringként, a kimenete pedig a 30 év feletti emberek száma a mai napon.
10. feladat: Írjunk egy hazArak(s) nevű függvényt, amelynek bemenete egy szrting. Ez a sztring egy excel fájl neve, amelyről felteheti, hogy az aktuális munkakönyvtárban van. Az excel-táblázat soraiban eladó ingatlanok adatai találhatóak. Az első oszlopbanban az árak forintban, a második oszlopban az alapterület négyzetméterben, a harmadik oszlopban a szobák száma. A függvény kimenete legyen a 2 szobás ingatlanok átlag négyzetméterára. (Felteheti, hogy az xls fájlban csak számok vannak).
11. feladat: Írjunk olyan maganhangzo(s1) nevű függvényt amelynek bemenete egy s1 sztring és a függvény kimenete, hogy hány magánhangzó van s1-ben (csak az angol ábécé magánhangzóit ideértve).
12. feladat: Adott egy csv fájl, amiben egy ismeretlen, egész számokból álló mátrix elemei vannak (a mátrix nem feltételen négyzetes). Írjunk egy olyan nagyNegyzet(s) nevű függvényt, amelynek bemenete a fájl neve sztringként. A függvény keresse meg azon 3*3-as négyzetet a mátrixon belül, amelyben a számok összege a legnagyobb. A kimenet legyen ezen négyzet bal felső sarkának pozíciója.
13. feladat*: Írjunk egy flipP(A) nevű függvényt, amelynek bemenete egy négyzetes mátrix. A kimenet legyen ezen mátrix (1,n), (n,1) elemeket átmenő átlójára tükrözöttje.
Példa: flipP([1 2 3; 4 5 6; 7 8 9]) kimenete [9 6 3; 8 5 2; 7 4 1].