Hetedik labor: Hipotézisvizsgálat

Contents

Bevezető: polimorf függvények

Láttuk, hogy a beépített gyári függvényeket többféleképpen is meg lehet hívni. Például a

rand

ans =

    0.1162

egy darab 0 és 1 közötti véletlen számot ad, míg

rand(4)

ans =

    0.4886    0.8244    0.1911    0.8284
    0.3474    0.1731    0.0504    0.9085
    0.7739    0.8636    0.5484    0.7053
    0.2853    0.9261    0.0095    0.2433

egy 4*4-es mátrixot,

rand(3,4)

ans =

    0.5892    0.6062    0.5601    0.4319
    0.9389    0.7924    0.0007    0.4307
    0.8955    0.8362    0.2513    0.8752

pedig egy 3*4-eset.

Ezt nevezik polimorf függvénynek: többféle számú bemenettel is működik, a kimenet pedig függ a meghívás módjától. Mi is készíthetünk ilyen függvényeket a nargin parancs felhasználásával. A nargin parancsot a függvény belsejében kiadva megkapjuk, hogy hány bemenettel (argumentummal) hívták meg a függvényt.

Példa: készítsünk szorzótáblát. Ha két bemenettel hívták meg a függvényt, akkor n*m-eset, ha eggyel akkor négyzeteset. Ha nullával, akkor 10*10-eset.

function ki=szorzotabla(n,m)
 
if nargin==0 
    n=10;
    m=10;
elseif nargin==1
   m=n;
end

v1=1:n;
v2=1:m;
ki=v1'*v2;

A nargin parancs párja a nargout, ami a meghíváskori kimenetek számát adja vissza.

Alapfeladat

Az alapfeladatunk a következő: feltesszük egy mérhető mennyiségről, hogy az ismeretlen háttéreloszlása rendelkezik egy bizonyos tulajdonsággal. El szeretnénk dönteni, hogy tényleg rendelkezik-e ezen tulajdonsággal a háttéreloszlás.

Első példa feladat: Miért nem elég az átlag?

Egy gép gyufákat tölt a gyufásdobozokba. Persze nem kerül mindegyikbe ugyanannyi, egy 100 db-os dobozon gyakran olvasható a 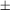$\pm$ 5% felirat. Ha le szeretnénk ellenőrizni a gépet, akkor megszámolhatjuk néhány dobozban a gyufák számát. Tegyük fel, hogy 10 dobozban rendre 98, 96,102, 104,92, 100, 108, 101, 99, 101 darab gyufát találtunk. Ezek átlaga:

meres1=[91, 96,102, 104,92, 100, 108, 101, 96, 101];
mean(meres1)

ans =

   99.1000

Kérdés, hogy ezek eltérése a 100-től a véletlennel magyarázható-e, vagy a 99.1-es átlag az jelenti, hogy a gép nagy átlagban is kevesebb gyufát csomagol? Mivel az általunk kiválasztott 10 dobozban lehet véletlenül is kevesebb 100-nál, ezért teljesen biztosak nem lehetünk a válaszunkban. De azt meg tudjuk mondani, hogy mekkora esélye van annak, hogy 10 ilyen számot kapjunk, ha valóban 100 az átlag. Erre valók a statisztikai próbák.

Statisztikai alapfogalmak

A fenti példánkban azt a feltevést, hogy átlagban 100 gyufa kerül egy dobozba nevezzük nullhipotézisnek. Általános esetben a nullhipotézis lehet egy olyan állítás, hogy a várható érték (hosszútávon az átlag a nszgyt szerint) egyenlő egy számmal, de akár az is, hogy két átlag egyenlő, vagy az, hogy két dolog független egymástól. Ezzel szemben áll az ellenhipotézis.

Ha a nullhipotézis az volt, hogy az eloszlás egy paramétere egyenlő egy bizonyos értékkel, akkor többféle ellenhipotézist állíthatunk fel: vagy azt, hogy nem egyenlő ezzel az értékkel (kétoldali ellenhipotézis), vagy azt, hogy szigorúan nagyobb (jobboldali ellenhipotézis), illetve szigorúan kisebb (baloldali ellenhipotézis). Ez utóbbi kettőt nevezik egyoldali ellenhipotézisnek.

Az statisztikai próba abból áll, hogy a mért értékekből kiszámítunk egy értéket (ezt nevezik statisztikai próbafüggvénynek), és ezen érték ismeretében vagy a nullhipotézist vagy az ellenhipotézist fogadjuk el igaznak.

Az eljárás folyamán kétféle hibát követhetünk el: vagy a nullhipotézis elutasítjuk, pedig igaz volt, ezt nevezik elsőfajú hibának. Vagy elfogadjuk a nullhipotézist, pedig hamis volt, ez a másodfajú hiba. Az elsőfajú hiba elkövetésének esélyét nevezzük szignifikancia-szintnek (gyakran jelölik $\alpha$-val). Annak esélye, hogy a nullhipotézis elfogadjuk, feltéve, hogy ő igaz a konfidenciaszint ($1-\alpha$). Általában elmondható, hogy az első és másodfajú hiba egymás ellen dolgozik, azaz ha magasabb konfidenciaszinten szeretnénk dönteni, azzal növeljük a másodfajú hiba esélyét. Mindkettőt egyszerre csökkenteni a minta elemszámának növelésével lehet.

Egymintás t-próba alkalmazása

Tegyük fel, hogy a gyufák száma normális eloszlást követ (ez nem egy nagy megszorítás általában a cht miatt). Ekkor a példafeladat kérdésére a egymintás, kétoldali t-próbával kereshetjük meg a választ, Matlabban a ttest a beépített függvény erre. Ennek visszatérési értéke 0, ha a nullhipotézis (a próba szerint) igaz, 1 hogy ha hamis:

ttest(meres1,100)

ans =

     0

A ttest alapból 5%-os szignifikanciaszinten dönt, ezt csak indokolt esetben változtassuk meg.

Ha csak arra vagyunk kíváncsiak, hogy kevesebbet tölt-e a gép a dobozokba, akkor baloldali egymintás t-próbára van szükségünk. Teszteljük azon nullhipotézist, hogy a várható érték 100, az ellenhipotézis legyen az, hogy a várható érték 100-nál kevesebb:

ttest(meres1,100,'Tail', 'left')

ans =

     0

Viszont ha az lenne a nullhipotézisünk, hogy a várható érték 98, azon ellenhipotézis mellett, hogy nem 98:

ttest(meres1,98)

ans =

     0

Ez az eredmény azt mutatja, hogy ebből a 10 mérésből nem tudjuk megkülönböztetni a 98 és a 100 várható értéket 5%-os szignifikanciaszinten. Ehhez több dobozt kell megszámolnunk, a Matlab azt is kiszámítja nekünk, hogy pontosan mennyit, ha tudjuk a mintánk szórását (legyen a mostani példánkban 5):

sampsizepwr('t',[100,5],98)

ans =

    68

A sampsizepwr függvény defaultja a 90%-os konfidenciaszint, ezt is állíthatjuk:

sampsizepwr('t',[100,5],98,0.95)

ans =

    84

A sampsizepwr függvény azt is kiszámítja nekünk, hogy ha adott elemszámú mintánk van (most éppen 10), akkor a két értékek milyen szignifikanciaszinten tudjuk megkülönböztetni egymástól:

sampsizepwr('t',[100,5],98,[],10)

ans =

    0.2051

Második mintapélda

Van összesen 20 darab nőstény garnélánk. Az első akváriumban lakik 9 darab, itt 25 fokos a vízhőmérséklet. Megmértük a "vemhességük" (a lárvák hasukhoz leengedésétől azok elengedéséig tartó időtartamot) időtartamát, és a következő értékeket kaptuk: 19, 17, 23, 23, 18, 20, 25, 22, 19 nap. A második akváriumban 21 fokos hőmérsékleten tartjuk őket, itt a az időtartamok: 18, 19, 26, 22, 19, 27, 24, 29, 23, 31, 27 nap. El szeretnénk dönteni, hogy hatással van-e a víz hőmérséklete az elengedésig eltelt napok számára.

Kétmintás t-próba

Most azt szeretnénk eldönteni, hogy két minta ugyanolyan várható értékű normális eloszlásból származik-e (a szórások egyenlőségét nem tesszük fel). Ehhez kétmintás kétoldali t-próbált alkalmazunk, a Matlabban ttest2:

akv25=[19, 17, 23, 23, 18, 20, 25, 22, 18];
mean(akv25)

ans =

   20.5556


akv21=[18, 19, 26, 22, 19, 27, 24, 29, 23, 31, 27 ];
mean(akv21)

ans =

   24.0909

Az átlagok eltérnek, de kérdés, hogy az eltérés magyarázható-e a vemhesség időtartamában lévő véletlennel. A t-próba alkalmazásával:

ttest2(akv21, akv25)

ans =

     1

95%-os konfidenciaszinten kijelenthetjük, hogy a víz hőmérséklete befolyásolja az elengedésig eltelt napok számát.

Órai feladatok

1. feladat: Írjunk olyan függvényt csere(v,a,b) nevű függvényt, amely kicseréli a v vektor minden a-val egyenlő elemét b-re. Ha csere(v,a) módon hívtuk meg, akkor minden a-val egyenlő elemet 1-re cseréljen. Ha csere(v) módon, akkor pedig minden 0-t cseréljen 1-re.

2. feladat Ellenőrizni szeretnénk, hogy igaz-e, hogy a 90 darabos papírzsebkendőben tényleg 90 db-ot csomagol-e a gyár. Tegyük fel, hogy a gép által csomagolt zsepik számának szórása 4.5.

3. feladat: Egy lázcsillapító gyógyszer hatásosságát szeretnénk tesztelni. Megmértük 10 ember hőmérsékletét a gyógyszer beadása előtt, az alábbi értékeket kaptuk: 38.1, 39.2, 37.9, 38.3, 39.5, 39.4, 38.5, 39.1, 38.4, 39.1 Fél órával a gyógyszer beadása után: 37.3, 36.9, 37.3, 37.2, 38.2, 37.4, 36.5, 37.3, 37.4, 36.8. Milyen nullhipotézist és ellenhipotézist kell feltennünk, hogy eldöntsük, hatásos-e a gyógyszer? Ellenőrizzük is Matlabbal a hipotézisünket!


Published with MATLAB® R2018b