Interpoláció
Contents
Az alapfeladat a következő: adott néhány pont, ahol ismert a függvény értéke (ezeket nevezzük mérési pontnak vagy alappontnak). Célunk, hogy olyan pontokra is meghatározzuk a függvényt, amelyekben nem mértem, ezt nevezzük interpolációs pontnak (ha a pont a két szélső mérési pont közé esik). Ha ezen intervallumon kívűl van, akkor extrapolációnak a nevezik feladatot.
Lineáris interpoláció
A mért értékeket összekötöm egy-egy szakasszal. Ezt e közelítést az interp1 függvény számolja ki:
x=[0 pi/3 pi/2]; % alappontok (itt mértem) y=[0 sqrt(3)/2 1]; % függvényértékek (ezeket az értékeket) hol=0.4; % mely pontokon szeretném közelíteni az ismeretlen függvényértékeket ert=interp1(x,y,hol)
ert =
0.3308
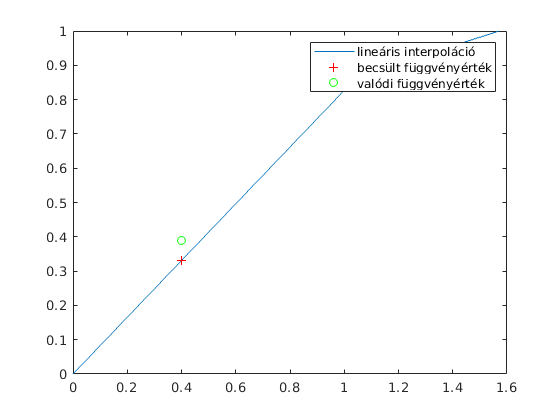
Ez a fajta közelítés bár gyorsan számolható, de cserébe nem túl pontos. Példaul, ha kiderül, hogy a közelítendő függvény valójában egy sin volt, akkor még a közelítés hibáját is meg tudom mondani:
plot(x,y, hol,ert,'r+',hol,sin(hol),'go') legend('lineáris interpoláció', 'becsült függvényérték', 'valódi függvényérték')
Spline interpoláció
Felhasználhatunk a közelítésre simább függvényt is, ezeket spline-nak hívják és a spline nevű függvénnyel lehet kiszámolni.
ert2=spline(x,y,hol)
ert2 =
0.4249
t=linspace(0,1); plot(t, sin(t),hol, ert,'r+',hol,ert2,'k*') % mérési pontokat összekötő vonal = legend('valódi függvény','becsült függvényérték (lin)', 'becsült függvényérték (spline)')
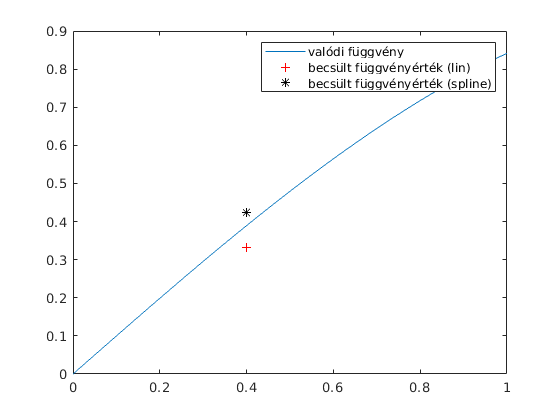
Összehasonlítva a kettőt láthatjuk, hogy a spline interpoláció sokkal jobb értékeket adott (bár némileg nagyobb a számolási igénye).
Adott fokszámú polinom illesztése
A polyfit paranccsal előre megadott fokszámú polinomot illeszthetünk az adatainkra, az alábbi példában egy parabolát. Ekkor a polyfit parancs a polinom együtthatóit adja vissza.
ehok=polyfit(x,y,2)
ehok = -0.3636 1.2077 0.0000
Ennek segítségével akár egyenes is illeszthető ha elsőfokú polinomot illeszthetünk.
A polyval függvény helyettesít be egy együtthatókkal adott polinomba:
ert3=polyval(ehok, hol)
ert3 =
0.4249
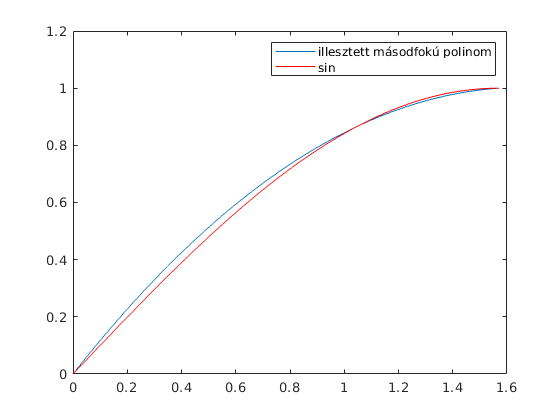
Itt ábrázolhatjuk az interpolációs polinomot is
t=linspace(0,pi/2); plot(t,polyval(ehok,t), t, sin(t),'r') legend('illesztett másodfokú polinom', 'sin')
Viszont...
t=linspace(-1,5); plot(t,polyval(ehok,t), t, sin(t),'r') legend('illesztett másodfokú polinom', 'sin')
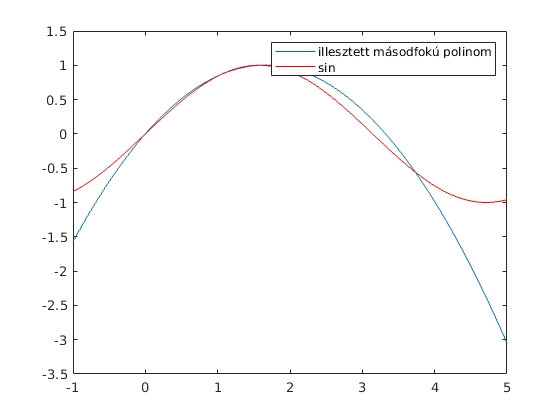
az extrapoláció (olyan pontban becsülni a függvényértékeket ami kívűl esik a mérési tartományon) kényes feladat, ha lehet kerüljük.
Órai feladatok
1.feladat: Írjunk olyan linkoz(v1,v2) nevű függvényt, melynek első bemente az alappontok egy vektorban sorban elrendezve, a második pedig a mért értékek vektora. A függvény határozza meg ezen értékekre legjobban illeszkedő egyenest, és ábrázolja is a pontokkal együtt. A függvény kimenete legyen az egyenes meredeksége.
2. feladat: Vegyük az (0.5, 1, 1.5, 2, 2.5, 3, 3.5) alappontkat, és a (3.27, 6.1, 9.7, 12.9, 15.1, 19.4, 21.3) mért értékeket. Írjon egy olyan függvényt, ami a legkisebb négyzetes értelemben legjobban közlítő n-edfokú polinomot ábrázolja a pontokkal együtt, majd menti is a képet egy jpg fájlba.
3.feladat: Írjunk olyan rungell(n) nevű függvényt, melynek bemenete egy n pozitív egész. A függvény interpolálja egy (n-1)-edfokú polinommal a 1/(1+x^2)függvényt az [-5,5] intervallumon vett n darab egyforma távolságra lévő ponton. Ábrázoljuk az eredeti függvényt és az interpoláló polinomot is a [-5,5] szakaszon. Küldjék be az .m fájl és két darab .jpg képet az n=5 és n=20 értékekkel. Segítség: n=3 esetén a három alappont a -5,0,5 és a "mért értékek" 1/26, 1, 1/26, ekkor másodfokú polinommal kell interpolálni).
4. feladat: Írjunk olyan interpolals(x,y,x0) nevű függvény Matlabban, amelynek bemeneti közül az első valós számokból álló sorvektor, a második bemenet pedig egy függvény helyettesítési értékei ezen pontokban szintén egy sorvektorban adva. A függvény kimenete legyen az ezen pontokra illesztett spline interpoláló polinom helyettesítési értéke az x0 pontban.