Contents
1.feladat
A kőhajításnál vegyük figyelembe a légellenállást is, ami jó közelítéssel a sebességgel egyenesen arányos (valamely k arányossági tényezővel), azaz most y''(t)=-9.8-k*y'(t). Ezt átírjuk rendszerré, hasonlóan az előbbiekhez a sebesség lesz az új változó, azaz: y'=v; v'=-9.8-k*v; A k értéke legyen 0.1. Derítsük ki, hogy mennyi idő alatt esik le a kő a földre.
MEGOLDÁS
function dyv = ko2(t,yv) %yv(1), a magasság: y(t) %yv(2) a függőleges sebesség: v(t) k=0.1; dyv = [yv(2); -9.8-k*yv(2)]; %fontos, hogy oszlopvektorként adjuk meg
function [ertek,megalle,irany] = esemeny(t,y) % Ez a függvény veszi észre, hogy elérjük a 0 magasságot, % és megállítja a megoldót ekkor. ertek = y(1)-0; % a 0 magasságot keresem, de lehetne más érték is megalle = 1; % állítsa-e meg a megoldót irany = 0; % csak ha csökken: -1, bármikor amikor eléri: 0, csak ha nő: 1
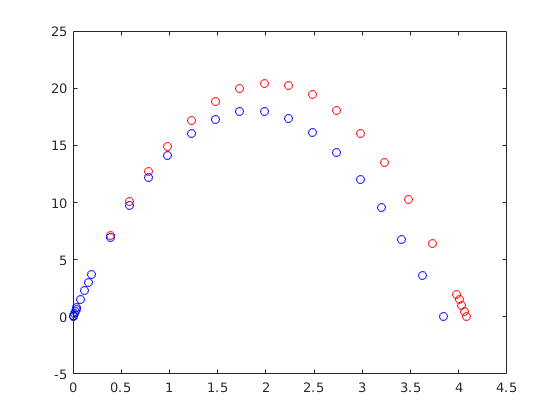
beallitasok = odeset('Events',@esemeny); [T4,Y4] = ode45(@ko,[0 10],[0,20],beallitasok); [T5,Y5] = ode45(@ko2,[0 10],[0,20],beallitasok); plot(T4,Y4(:,1), 'rO') T4(end) hold on plot(T5,Y5(:,1), 'bO') T5(end) hold off
ans =
4.0816
ans =
3.8369
2.feladat
Tegyük fel, hogy két halfaj él egy területen: egy növényevő és egy ragadozó. Ekkor a halászás hatását úgy írhatjuk le, hogy mindkét faj egy hányadát elveszítjük egy adott idő alatt. Ha Lotka-Volterra modellt használunk, akkor mindkét fajnál megjelenik negatív tag; a növényevőknél egy -e*N(t) illetve ragadozóknál egy -e*P(t) tag. Oldjuk meg ezen új egyenletet Matlabban, ha e=0.05. Ábrázoljuk az új rendszer fázisportréját a régivel egy képen.
MEGOLDÁS
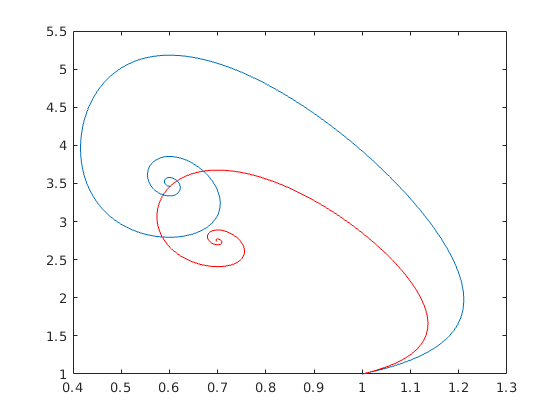
function dy = lotvol2(t,y) r=0.5; K=2; a=0.1; b=0.3; c=0.5; e=0.05; dy = [ r*(1-y(1)/K)*y(1)-a*y(1)*y(2)-e*y(1);... -b*y(2)+c*y(1)*y(2)-e*y(2)];
beallitasok = odeset('RelTol',1e-8); [T,Y]=ode45(@lotvol,[0,60],[1,1],beallitasok); [T2,Y2]=ode45(@lotvol2,[0,60],[1,1],beallitasok); plot(Y(:,1),Y(:,2)) plot(Y(:,1),Y(:,2)) hold on, plot(Y2(:,1),Y2(:,2),'r') hold off %Figyelemre méltó, hogy a növényevők száma nőtt...