labor12mo

1.feladat A Verlust-modellben legyen r=0.03, K=10. Tegyük fel, hogy a 0. időpillanatban a populációsűrűség N(0)=12. Állapítsuk meg az eseménykezelő segítségével, hogy mikor csökken a populációsűrűség először 10.5 alá!

A differenciálegyenletet definiáló függvények

function dy=verlust1fel(t,y)

r=0.03;
K=10;
dy=r*(1-y/K)*y;

Az eseményfigyelő függvény

function [ertek,megalle,irany] = esemeny1fel(t,y)


ertek = y-10.5; %ha lecsökken a populációsűrűség 10.5 alá     
megalle = 1;   
irany = -1;

A megoldó

beallitasok=odeset('Events',@esemeny1fel);
[T,Y] = ode45(@verlust1fel,[0 1000],12,beallitasok);
T(end)

ans =

   42.7922

2. feladat: Ismert, hogy ha a Lotka--Volterra-modellben a ragadozó nem elég hatékonyan használja fel a zsákmányt, akkor kihal. Ez történik például az r=0.5, K=2, a=0.1, b=0.3, c=0.1 paraméterek esetén. Állapítsuk meg az esemény-kezelő segítségével, hogy mikor csökken a ragadozók száma a [10, 10] kezdeti feltételből indulva 1 alá.

A differenciálegyenletet definiáló függvények

function dy = lotvol2fel(t,y)

r=0.5;
K=2;
a=0.1;
b=0.3;
c=0.1;

dy = [r*(1-y(1)/K)*y(1)-a*y(1)*y(2);...
      -b*y(2)+c*y(1)*y(2)];

Az eseményfigyelő függvény

function [ertek,megalle,irany] = esemeny2fel(t,y)


ertek = y(2)-1;     % a ragadozó sűrűsége 1 alatt
megalle = 1;   
irany = -1;

A megoldó

beallitasok=odeset('Events',@esemeny2fel);
[T,Y] = ode45(@lotvol2fel,[0 1000],[10,10],beallitasok);
T(end)

ans =

   10.9445

3.feladat: Tekintsük az y'(x)=y^2(x)-1, y(0)=0.5 kezdeti érték feladatot. Írjunk olyan diffKiert(z) nevű függvényt, amely megoldja a differenciálegyenletet, és a kimenete a megoldás (közelítő) értéke a z pontban, azaz y(z). A megoldást egyetlen függvénnyel készítsük el.

function ki=diffKiert(z)

[~,Y]=ode45(@(t,y) y^2-1,[0,z],0.5);
ki=Y(end);

end

4. feladat: Írjunk olyan kozelit(t,v) nevű függvényt, amelynek bemenetei sorvektorok. A t pontokban megmértük egy ismeretlen függvény értékeit, amelyről annyik tudunk, hogy a*sin(t)+b*sin(2t)+c*exp(-t) alakú, a mérési eredmények szerepelnek a v vektorban. A függvényünk kimenete legyen az a,b,c számok egyetlen oszlopvektorban.

function ki=kozelit(t,v)

E = [sin(t') sin(2*t') exp(-t')]; 

ki = E\(v');

5.feladat: Írjuk olyan kbSin1(n) függvényt, amelynek bemenete egy pozitív egész szám. A függvény készítse el a \sin függvény 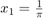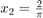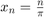$x_1=\frac{1}{\pi}$ , $x_2=\frac{2}{\pi}$ , $\dots$ , $x_n=\frac{n}{\pi}$ , alappontokra illeszkedő spline- interpolációját majd ez alapján adjon becslést a \sin(1) értékre, amely legyen a függvény kimenete.

function ki=kbSin1(n)

t=(1:n)/pi;
fvert=sin(t);

ki=spline(t,fvert,1);

6. feladat: Írjunk egy olyan teglaLap(a,b,x0,y0) nevű függvényt amelynek bemenetei valós számok. A függvény rajzoljon ki egy olyan téglalapot, amelynek bal alsó sarka az (x_0, y_0) pont, az x tengellyel párhuzamos oldala a, az y tengellyel párhuzamos oldala pedig b hosszú. Ha csak két kimenettel hívtuk meg, akkor a bal alsó sarok legyen az origó, ha csak eggyel akkor a bal alsó sarok legyen az (1,1) és rajzoljunk a oldalhosszú négyzetet. A függvények ne legyen kimenete.

function teglaLap(a,b,x0,y0)

if nargin==2
    x0=0;
    y0=0;
elseif nargin==1
    x0=1;
    y0=1;
    b=a;
end

plot([x0,x0+a],[y0,y0], [x0+a,x0+a],[y0,y0+b], [x0,x0],[y0,y0+b],[x0,x0+a],[y0+b,y0+b]);
axis([x0-1, x0+a+1,y0-1,y0+b+1],'equal');

7. feladat: Írjunk egy olyan egeszRitka(s) nevű függvényt, amelynek bemenete egy csv fájl neve sztringként. A függvény olvassa be egy mátrixba a fájlban található számokat. Ha az összes számok közül a nullák aránya meghaladja a 90%-ot, akkorezt írja ki a képernyőre. A függvény kimenete legyen az így kapott mátrix.

function adatok=egeszRitka(s)

adatok=dlmread(s);

nullakszama=sum(sum(adatok==0));

if nullakszama/(size(adatok,1)*size(adatok,2))>0.9
    fprintf('Sok a nulla \n');
end

8. feladat: Írjunk egy szigN(s) nevű függvényt, amelynek bemenete egy xls fájl neve sztringként. A fájl mérési eredményeket tartalmaz 2 oszlopban. Az első sorban egy-egy hőmérsékletérték található alatta pedig a mért hosszak centiméterben 150 tárgyra. Állapítsuk meg, hogy a két különböző hőmérséklet mellett mért hosszak szignifikánsan különböznek-e.

function szigN(s)

hosszak=xlsread(s);

elso=hosszak(2:151,1);
masodik=hosszak(2:151,2);

hip=ttest2(elso, masodik);

if hip==0 
    fprintf('A hosszak nem különböznek szignifikánsan\n')
else
    fprintf('A hosszak szignifikánsan különboznek')
end

9. Hány hal van a kois.jpg képen?