Első labor
Contents
Futásidő jellemzése
1.feladat Egy program futásidejére a 2,3, .. , 10 hosszú bemenetekre rendre 5, 16, 39, 76, 131, 209, 312, 444, 610 mp-t kaptunk. Feltéve, hogy polinomidejű algoritmusról van szó, adjunk becslést a kitevőre.
%{ MEGOLDÁS t=2:10; v=[5, 16, 39, 76, 131, 209, 312, 444, 610]; plot(log(t),log(v)), tools-> basic fitting-> linear & show equations %}
Első tesztfeladat a hátizsák-problémára
% Súlyok 1, 10, 1, 10,... % Értékek: 10, 1, 10, 1,... % Kapacitás: a tárgyak számának fele targyakszama=30; sulyok=ones(1, targyakszama); sulyok(2:2:end)=10; ertekek=ones(1, targyakszama); ertekek(1:2:end)=10; kapacitas=targyakszama*2.5; % ekkor az optimális pakolás 5.2*n lesz (156 itt) generacio=100; populaciomeret=30; keresztezesvaloszinusege=0.9; mutaciovaloszinusege=0.03; [fit, vege]=hatizsak_elitista(sulyok,ertekek,kapacitas,... keresztezesvaloszinusege, mutaciovaloszinusege, generacio, populaciomeret,5); vege(1,:) max(max(fit)) plot(1:generacio, sum(fit)/populaciomeret,'b', 1:generacio, max(fit,[],1),'g' ) xlabel('generációk száma') ylabel('fitnesz')
ans =
Columns 1 through 13
1 1 1 0 1 0 1 0 1 0 1 0 1
Columns 14 through 26
1 1 0 1 1 1 0 1 1 1 0 1 0
Columns 27 through 30
1 1 1 1
ans =
156

Második tesztfeladat
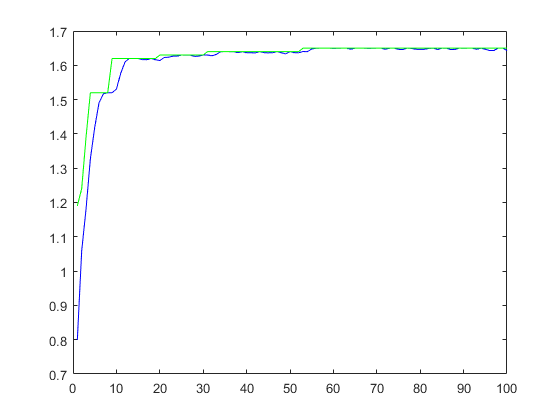
kapacitas=targyakszama*0.5; [fit, vege]=hatizsak_elitista(sulyok,ertekek,kapacitas,... keresztezesvaloszinusege, mutaciovaloszinusege, generacio, populaciomeret,5); vege(1,:) max(max(fit)) plot(1:generacio, sum(fit)/populaciomeret,'b',... 1:generacio, max(fit,[],1),'g' ) % Hogyan lehetne ezen javítani?
ans =
Columns 1 through 13
1 1 1 1 1 1 1 1 1 1 1 1 1
Columns 14 through 26
1 1 1 1 1 1 1 1 1 1 1 1 1
Columns 27 through 30
1 1 1 1
ans =
1.650000000000000
Paraméterek változtatása
Tegyük fel, hogy megváltoztatunk egy operátort egy genetikus algoritmusban. Hogyan tudnánk mérni, hogyan változott az algoritmus teljesítménye?
a=randn(1,10); % 10 darab normális eloszlású véletlen szám, 1 szórással a2=a-0.5; % -0.5 várható értékkel, szórás változatlan a3=a-2; % -2 várható értékkel b=randn(1,10); % 0 várható értékkel aa=randn(1,100); % 100 darab normális eloszlású véletlen szám, 1 szórással aa2=aa-0.5; bb=randn(1,100);
Vehetjük a minták átlagát a mean() parancssal, de ha az egyik nagyobb, az lehet az adatok véletlen szórásából (ami kicsi mintaméretnél különösen nagy). Az mintából számolt átlag egyben a legjobb tippünk a várható értékre is, azaz arra, hogy nagyon sok próbálkozás esetén mennyi lesz az átlag.
mean(a)
ans = -0.148645148273699
mean(b)
ans = 0.319834086398782
mean(aa)
ans = -0.064208184038062
mean(bb)
ans = -0.077617946811571
T-próba alkalmazása
Legyen v és w két normális eloszlásból származó vektor (például futásidők vagy megtalált legjobb megoldások lehetnek benne egy genetikus algoritmusból). Ekkor annak eldöntésére, hogy ugyanannyi-e a várható értékük, 2 mintás t-próbát alkalmazunk. Ez érzékeny a különböző átlagokra, de figyelembe veszi a természetes ingadozást is. Itt a 0 jenetése: azonos várható értékűek 95%-os valószínűséggel, 1 jelentése: különböző várható értékűek 95%-os valószínűséggel. Azaz van-e szignifikáns eltérés a két minta között, vagy csak a véletlen szórásból adodó ingadozás.
Azonos várható érték, kis elemszám:
ttest2(a,b)
ans =
0
Azonos várható érték, nagy elemszám:
ttest2(aa,bb)
ans =
0
Kicsit különböző várható érték, kis elemszám:
ttest2(a2,b)
ans =
0
Nagyon különböző várható érték, kis elemszám:
ttest2(a3,b)
ans =
1
Kicsit különböző várható érték, nagy elemszám:
ttest2(aa2,bb)
ans =
1
Tanulság: nagy méretű minta kell, különben nem működik (igazából nem elég érzékeny) a statisztikai próba. Ennek legyártása persze költséges. Ugyanakkor statisztikai próba nélkül "szemre" nem lehet kiértékelni az eltérést.
A genetikus algoritmus kódja
function [fitneszek, vegall]=hatizsak_elitista(sulyvektor,ertekvektor,... sulykorlat,keresztezesval,mutacioval,generaciokszama,populaciomeret,... tournamentmeret) % Hátizsák probléma: adott n db tárgy, s1,s2,..sn súlyúak, v1,v2,...,vn % értékek, és egy K teherbírású hátizsák. A cél, hogy kiválasszunk néhány % tárgyat, hogy azok összsúlya súlykorlátot ne haladja meg, és az % összértékük maximális legyen. % A függvény meghívásának módja: hatizsak_egyszeru(sulyvektor,ertekvektor,sulykorlat,... % keresztezesval,mutacioval,generaciokszama,populaciomeret,tournamentmeret), % ahol % sulyvektor: egy sorvektor, amelyben lévő pozitív valósak adják a tárgyak súlyát % ertekvektor : egy sorvektor, amelyben lévő pozitív valósak adják a % tárgyak értékét % Ezen két vektor elemszámának egyformának kell lennie % sulykorlat: pozitív valós szám, a kapacitást adja meg % keresztezesval, mutacioval, generaciokszama, populaciomeret: a genetikus % algoritmus kötelezően megadandó paraméretei % tournamentmeret: az egy körben kiválasztott potenciális szülők száma if length(sulyvektor)~=length(ertekvektor) || mutacioval<0 || mutacioval>1 ... || keresztezesval<0 || keresztezesval>1 || generaciokszama <0 ||... populaciomeret<0 || mod(populaciomeret,2)==1 error('Rossz bemeneti paraméterek'); end %A bemeneti paraméterek ellenőrzése %A kezdeti populáció létrehozása targyakszama=length(sulyvektor); populacio=ceil(rand(populaciomeret,targyakszama)-0.5); % a populáció egy mátrix, benne soronként vannak az egyes egyedek fitneszek=zeros(populaciomeret, generaciokszama); for i=1:generaciokszama populaciofitnesz=fitnesz(populacio,sulyvektor,ertekvektor,sulykorlat); fitneszek(:,i)=populaciofitnesz; [elitertek, elitpoz]=max(populaciofitnesz); elitegyed=populacio(elitpoz, :); populacio=kivalaszt_tournament(populacio,populaciofitnesz,tournamentmeret); populacio=keresztez_egypontos(populacio,keresztezesval); populacio=mutacio_egybit(populacio,mutacioval); populacio(1,:)=elitegyed; end vegall=populacio; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Tagfüggvények %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function populaciofitnesz=fitnesz(populacio,sulyvektor,ertekvektor,sulykorlat) populaciofitnesz=zeros(size(populacio,1),1); % preallokáció for i=1:size(populacio,1) if dot(populacio(i,:),sulyvektor)>sulykorlat populaciofitnesz(i)=0.01*dot(populacio(i,:),ertekvektor); else populaciofitnesz(i)=dot(populacio(i,:),ertekvektor); end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function szulok=kivalaszt_tournament(populacio,populaciofitnesz,tournamentmeret) szulok=zeros(size(populacio,1),size(populacio,2)); for i=1:size(populacio,1) poziciok=ceil(size(populacio,1)*rand(tournamentmeret,1)); [legjobbpoz,legjobbhely]=max(populaciofitnesz(poziciok)); szulok(i,:)=populacio(poziciok(legjobbhely),:); end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function utod=keresztez_egypontos(populacio,keresztezesval) utod=populacio; n=size(populacio,2); for i=1:2:size(populacio,1) if rand<keresztezesval vagopont=ceil((n-1)*rand); utod(i,:)=[populacio(i,1:vagopont), populacio(i+1,vagopont+1:n)]; utod(i+1,:)=[populacio(i+1,1:vagopont), populacio(i,vagopont+1:n)]; else utod(i,:)=populacio(i,:); utod(i+1,:)=populacio(i+1,:); end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function utod=keresztez_uniform(populacio,keresztezesval) utod=populacio; for i=1:2:size(populacio,1) if rand<keresztezesval for j=1:size(populacio,2) if rand<0.5 utod(i,j)=populacio(i+1,j); utod(i+1,j)=populacio(i,j); end end end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function utod=mutacio_egybit(populacio,mutacioval) utod=populacio; n=size(populacio,2); for i=1:size(populacio,1); if rand<mutacioval pozicio=ceil(n*rand); if populacio(i,pozicio)==0; utod(i,pozicio)=1; else utod(i,pozicio)=0; end end end