Contents

Negyedik labor

Tesztelő az utazóügynök problémához

tic
keresztezesvsz=1;
mutaciovsz=0.3;
generaciokszama=100;
populaciomeret=30;
tournamentmeret=5;

meret=14; % páros!
ismetlesekszama=30;

utak_e=zeros(ismetlesekszama,1);
utak_i=zeros(ismetlesekszama,1);

utak2_e=zeros(ismetlesekszama,1);
utak2_i=zeros(ismetlesekszama,1);

utak3_e=zeros(ismetlesekszama,1);
utak3_i=zeros(ismetlesekszama,1);

for i=1:ismetlesekszama

    [E, I]=egyszerukor(meret);
    [E2, I2]=laposfitnesz(meret);
    [E3, I3]=nemmoho(meret);

    [m,~]=utazougynok(E,keresztezesvsz,mutaciovsz,generaciokszama,populaciomeret, tournamentmeret);
    utak_e(i)=min(m);

    [m,~]=utazougynok(I,keresztezesvsz,mutaciovsz,generaciokszama,populaciomeret, tournamentmeret);
    utak_i(i)=min(m);

    [m,~]=utazougynok(E2,keresztezesvsz,mutaciovsz,generaciokszama,populaciomeret, tournamentmeret);
    utak2_e(i)=min(m);

    [m,~]=utazougynok(I2,keresztezesvsz,mutaciovsz,generaciokszama,populaciomeret, tournamentmeret);
    utak2_i(i)=min(m);

    [m,~]=utazougynok(E3,keresztezesvsz,mutaciovsz,generaciokszama,populaciomeret, tournamentmeret);
    utak3_e(i)=min(m);

    [m,~]=utazougynok(I3,keresztezesvsz,mutaciovsz,generaciokszama,populaciomeret, tournamentmeret);
    utak3_i(i)=min(m);
end
toc
fprintf('Ha a drága utak 7 és 10 között vannak: \n')
fprintf('Ennyiszer találta meg az optimumot az egyszerű körre: %d ennyi próbálkozásból: %d\n ',  sum(utak_e==meret), ismetlesekszama);
fprintf('Ennyiszer találta meg az optimumot az izomorf gráfra: %d ennyi próbálkozásból: %d\n ',  sum(utak_i==meret), ismetlesekszama);
fprintf('Ha a drága utak 2 és 5 között vannak: \n')
fprintf('Ennyiszer találta meg az optimumot az egyszerű körre: %d ennyi próbálkozásból: %d\n ',  sum(utak2_e==meret), ismetlesekszama);
fprintf('Ennyiszer találta meg az optimumot az izomorf gráfra: %d ennyi próbálkozásból: %d\n ',  sum(utak2_i==meret), ismetlesekszama);
fprintf('Amire a mohó nem működik: \n')
fprintf('Ennyiszer találta meg az optimumot az egyszerű körre: %d ennyi próbálkozásból: %d\n ',  sum(utak3_e==2*meret), ismetlesekszama);
fprintf('Ennyiszer találta meg az optimumot az izomorf gráfra: %d ennyi próbálkozásból: %d\n ',  sum(utak3_i==2*meret), ismetlesekszama);

Elapsed time is 9.114193 seconds.
Ha a drága utak 7 és 10 között vannak: 
Ennyiszer találta meg az optimumot az egyszerű körre: 30 ennyi próbálkozásból: 30
 Ennyiszer találta meg az optimumot az izomorf gráfra: 30 ennyi próbálkozásból: 30
 Ha a drága utak 2 és 5 között vannak: 
Ennyiszer találta meg az optimumot az egyszerű körre: 22 ennyi próbálkozásból: 30
 Ennyiszer találta meg az optimumot az izomorf gráfra: 16 ennyi próbálkozásból: 30
 Amire a mohó nem működik: 
Ennyiszer találta meg az optimumot az egyszerű körre: 20 ennyi próbálkozásból: 30
 Ennyiszer találta meg az optimumot az izomorf gráfra: 18 ennyi próbálkozásból: 30
 

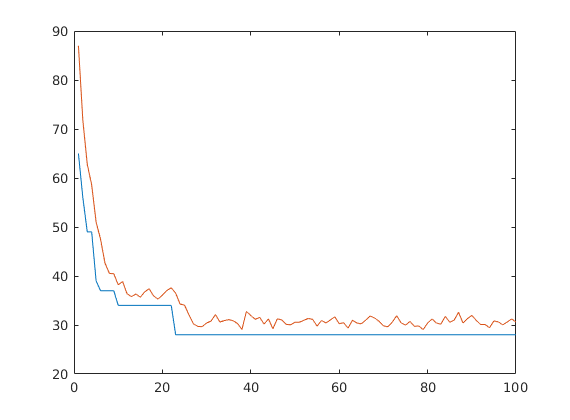
A futások vizsgalatához

[m,a]=utazougynok(I3,keresztezesvsz,mutaciovsz,generaciokszama,populaciomeret, tournamentmeret);
plot(1:generaciokszama, m, 1:generaciokszama, a)

A tesztfeladatok

Meredek fitnesz

function [ egyszeru, izomorf]=egyszerukor(meret)

% skálázható egyszerű kör

D=randi([7 10],meret);
egyszeru=triu(D,2)+triu(D,2)';

for j=1:meret-1
    egyszeru(j+1,j)=1;
end

for j=2:meret
    egyszeru(j-1,j)=1;
end

egyszeru(1,meret)=1;
egyszeru(meret,1)=1;

% izometria
p=randperm(meret);
permutacio=zeros(meret);

for j=1:meret
    permutacio(p(j),j)=1;
end

izomorf=permutacio'*egyszeru*permutacio;

Lapos fitnesz

function [ egyszeru, izomorf]=laposfitnesz(meret)

D=randi([2 5],meret);
egyszeru=triu(D,2)+triu(D,2)';

for j=1:meret-1
    egyszeru(j+1,j)=1;
end

for j=2:meret
    egyszeru(j-1,j)=1;
end

egyszeru(1,meret)=1;
egyszeru(meret,1)=1;

% izometria
p=randperm(meret);
permutacio=zeros(meret);

for j=1:meret
    permutacio(p(j),j)=1;
end

izomorf=permutacio'*egyszeru*permutacio;

Harmadik tesztfeladat

function [ egyszeru, izomorf]=nemmoho(meret)

% a mohó algortimus nagyon elrontja

D=randi([6 9],meret);
egyszeru=triu(D,2)+triu(D,2)';

for j=1:meret-1
    egyszeru(j+1,j)=2;
end

for j=1:2:meret-2
    egyszeru(j+2,j)=1;
end

for j=2:meret
    egyszeru(j-1,j)=2;
end

for j=3:2:meret
    egyszeru(j-2,j)=1;
end

egyszeru(1,meret)=2;
egyszeru(meret,1)=2;

% izometria
p=randperm(meret);
permutacio=zeros(meret);

for j=1:meret
    permutacio(p(j),j)=1;
end

izomorf=permutacio'*egyszeru*permutacio;

Megoldó: elitista, tournament kiválasztással, EX keresztezéssel

function [maxfit,atlagfit]=utazougynok(g,pc,pm,gen,pop, tournamentmeret)
% bemeneti paraméterek
% G: az élsúlyozott gráf szomszédsági mátrixa
% pc: a keresztezés valószínűsége
% pm: a mutáció valószónűsége
% gen: a generációk száma 
% pop: a populáció egyedszáma 
% tournamentmeret: az egy körben kiválasztott szülőjelöltek száma


if pm<0 || pm>1 || pc<0 || pc>1 || gen <0 || pop<0 
 error('Rossz bemenő paraméterek'); end 



n=length(g); %a gráf csúcsainak a száma
populacio=zeros(pop,n);

for i=1:pop
populacio(i,:)=randperm(n); % egy egyed egy sor
end


atlagfit=zeros(1,gen);
maxfit=zeros(1,gen);

for i=1:gen
    f=fittnesz(populacio,g,n,pop);
    
    atlagfit(i)=mean(f);
    [maxfit(i), elitpoz]=min(f);
    
    elitegyed=populacio(elitpoz,:);
    
    populacio=kivalaszt_tournament(populacio,f,tournamentmeret);
    populacio=keresztez(populacio,pc,pop);
    populacio=mutacio_inverzio(populacio,n,pm,pop);
    
    populacio(1,:)=elitegyed;
end

%-----------------------------------------------------------------------

function f=fittnesz(A,g,n,pop)

f=zeros(pop,1);

for i=1:pop    
    suly=g(A(i,n),A(i,1));
    
    for j=1:n-1
        suly=suly+g(A(i,j),A(i,j+1));      
    end   
    
    f(i)=suly;
end

%-------------------------------------------------------------------------

function szulok=kivalaszt_tournament(populacio,populaciofitnesz,k)

szulok=zeros(size(populacio));

for i=1:size(populacio,1)
    poziciok=ceil(size(populacio,1)*rand(k,1));
    [~,legjobbhely]=min(populaciofitnesz(poziciok));
    szulok(i,:)=populacio(poziciok(legjobbhely),:);
end

%------------------------------------------------------------------------

function B=keresztez(A,pc,pop)


B=A;

for i=1:2:pop

    if rand<pc % ha van keresztezés
    
       B(i,:)  =ex(A(i,:),A(i+1,:));
       B(i+1,:)=ex(A(i,:),A(i+1,:));
    end
end

%-------------------------------------------------------------------------

function A=mutacio_inverzio(B,n,pm,pop)
% egy kromoszomán belül kiválaszt egy szakaszt, majd megfordítja
A=B;
for i=1:pop
    if rand<pm
        a=ceil((n-1)*rand);
        b=ceil((n-1)*rand);
        if a<b
            vp1=a; vp2=b; %végpontok
        else
            vp1=b; vp2=a;
        end 
        A(i,vp1:vp2)=fliplr(B(i,vp1:vp2)); 
    end
end

%------------------------------------------------------------------------
function utod=ex(p1,p2)

n=length(p1);
ellista=zeros(n,4);
voltmar=zeros(n,1); %egy flag

%éllista elkészítése
for i=1:n
    if i==1
        ellista(p1(i),1)=p1(n);
        ellista(p1(i),2)=p1(2);
    elseif i==n
        ellista(p1(i),1)=p1(n-1);
        ellista(p1(i),2)=p1(1);
    else
        ellista(p1(i),1)=p1(i+1);
        ellista(p1(i),2)=p1(i-1);
    end
    
    if i==1
        ellista(p2(i),3)=p2(n);
        ellista(p2(i),4)=p2(2);
    elseif i==n
        ellista(p2(i),3)=p2(n-1);
        ellista(p2(i),4)=p2(1);
    else
        ellista(p2(i),3)=p2(i+1);
        ellista(p2(i),4)=p2(i-1);
    end
end

ellista=sort(ellista')'; %rendezett éllista, lehetnek benne duplák

% most jön a permutáció felépítése
utod=zeros(1,n);

pozicio=randi(n);


for j=1:n    
    utod(j)=pozicio;
    voltmar(pozicio)=1; % bejelölöm, hogy már volt
    if sum(voltmar)==n, return, end %
    ellista(ellista==pozicio)=0; % kitörlöm az aktuális elemre hivatkozást
    % Van közös csúcs? Segítség, hogy az éllista rendezett
    if ellista(pozicio,1)==ellista(pozicio,2)  && ellista(pozicio,1)~=0
        tmp= pozicio;
        pozicio=ellista(pozicio,1);
        ellista(tmp,:)=[0 0 0 0];
        continue;
    elseif ellista(pozicio,2)==ellista(pozicio,3) && ellista(pozicio,2)~=0
        tmp= pozicio;
        pozicio=ellista(pozicio,2);
        ellista(tmp,:)=[0 0 0 0];
        continue;
    elseif ellista(pozicio,3)==ellista(pozicio,4) && ellista(pozicio,3)~=0
        tmp= pozicio;
        pozicio=ellista(pozicio,3);
        ellista(tmp,:)=[0 0 0 0];
        continue;
    end
    % ha nincs közös él, akkor megnézem a listahosszakat
    mlh=zeros(1,4);
    for i=1:4
        if  ellista(pozicio,i)==0
            mlh(i)=5;
        else
        mlh(i)=sum(ellista(ellista(pozicio,i),:)~=0);
        end
    end
    
    if sum(mlh)==20 % Ha üres mindenki, akkor új véletlen pozició kell, az utód segítségével
        ranpoz=randi(n);
        while voltmar(ranpoz) % és olyan ami még nem szerepelt
            ranpoz=randi(n);
        end
        pozicio=ranpoz;
        continue; % itt nem kell nullázni az előző pozició listáját
    end
    % egyébként meg kell keresni a maradékban a legrövidebb listahosszt
  
    mini=min(mlh);   % a legrövidebb lista
    minipoz=(mlh==mini);% a legrövidebb lista 
    ranpoz=randi(4);
    while ~minipoz(ranpoz) % véletlen a minimális hosszúak közül
        ranpoz=randi(4); 
    end
    
    tmp= pozicio;
    pozicio=ellista(pozicio,ranpoz);  
    ellista(tmp,:)=[0 0 0 0];
end

Az n királynő probléma branchinggel

function [elrendezesek,joelrendezes]=queens(n)

sor=1; 
oszlop=zeros(1,n); 
utolso=0; 
utes=0; 
joelrendezes=[];
elrendezesek=0; 

while sor~=1 || utolso~=n

    if utolso<n
        oszlop(sor)=utolso+1;
        sor=sor+1; 
        t=1; 
    elseif sor==n+1
        elrendezesek=elrendezesek+1;
        joelrendezes=[joelrendezes; oszlop];
        sor=sor-1; 
        t=oszlop(sor)+1;
    elseif utolso==n
        sor=sor-1;
        t=oszlop(sor)+1; 
    end

    
    for i=t:n 
        utes=0;  
        for j=1:sor-1 
            if (oszlop(j)==i || abs(sor-j)==abs(i-oszlop(j)))
                utes=1; 
            end
        end
        if utes==0
            break
        end
    end
    
    if utes==0 
        utolso=i-1;
    else
        utolso=n; 
    end

end

Published with MATLAB® R2018b