Második labor
Contents
Tesztfeladat a szkémaszámoláshoz
Súlyok 1, 10, 1, 10, ...
Értékek: 10, 1, 10, 1, ...
targyakszama=10; sulyok=ones(1, targyakszama); sulyok(2:2:end)=10; ertekek=ones(1, targyakszama); ertekek(1:2:end)=10; generacio=30; populaciomeret=10; keresztezesvaloszinusege=0.9; mutaciovaloszinusege=0.03; kapacitas=targyakszama*2.5; % ekkor az optimális pakolás 5.2*n lesz, itt 52 tic [populacio,maximumfitnesz,atlagfitnesz, szkemaszam]=hatizsakGenetikusSzkema... (sulyok,ertekek,kapacitas,keresztezesvaloszinusege, mutaciovaloszinusege, generacio, populaciomeret); toc subplot(2,1,1) plot(1:generacio, szkemaszam) ylabel('Illeszkedő szkémák száma') xlabel('Generáció') subplot(2,1,2) plot(1:generacio, maximumfitnesz, 1:generacio, atlagfitnesz, 1:generacio, 52*ones(1,generacio)) ylabel('Fitnesz') xlabel('Generáció')
Elapsed time is 6.111881 seconds.
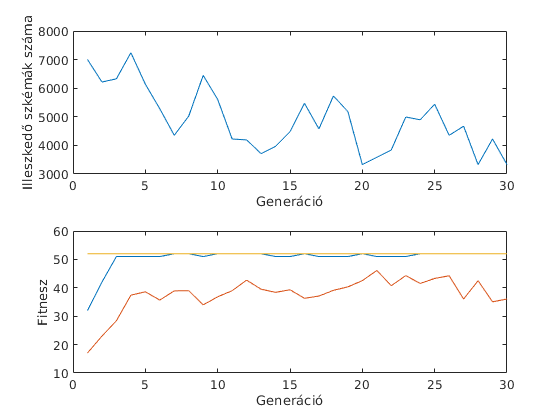
Tesztelés és validáció
A tesztelés célja a paraméterek optimalizálása (ide értve a fitneszfüggvény is), a validáció célja annak eldöntése, hogy mennyire jó általános feladatra az általunk készített algoritmus. Azaz a tesztfeladaton egy előre ismert optimumú függvényt tesztelünk, minnél többet az optimális paraméterek/fitneszfüggvény meghatározása céljából. A validáció folyamán egy (vagy több) előre nem ismert feladattal próbáljuk eldönteni, hogy jó-e (igazából jól általánosítható-e) az algoritmusunk a majdani, már nem ismert optimumú feladatra.
Órai feladat
Gondoljuk meg, hogyan reprezentálnánk az alábbi kérdés pontenciális megoldásait. Milyen tesztet és validációt javasolnánk?
Szeretnénk 1-hibajavító kódot készítése 8 hosszú bitsorozaton. Mekkora lehet maximum a szavak száma? Akkor lesz a kódunk 1 hibajavító, ha bármely 2 kódszó Hamming-távolsága legalább 3. A Hamming-korlátból tudjuk, hogy a szavak maximális száma 28 ebben a konkrét esetben.
A szkémaszámoló kódja
function [populacio,maximumfitnesz,atlagfitnesz, szkemaszam]=hatizsakGenetikusSzkema(sulyvektor,... ertekvektor,sulykorlat,keresztezesval,mutacioval,generaciokszama,populaciomeret) % Hátizsák-probléma: adott n db tárgy, s1,s2,..sn súlyúak, v1,v2,...,vn % értékűek, és egy fix teherbírású hátizsák. A cél, hogy kiválasszunk néhány % tárgyat, hogy azok összsúlya a sulykorlatott ne haladja meg, és az összértékük maximális % legyen. if length(sulyvektor)~=length(ertekvektor) || mutacioval<0 || mutacioval>1 ... || keresztezesval<0 || keresztezesval>1 || generaciokszama <0 ||... populaciomeret<0 || mod(populaciomeret,2)==1 error('Rossz bemenő paraméterek'); end %A bemeneti paraméterek ellenőrzése %A kezdeti populáció létrehozása targyakszama=length(sulyvektor); populacio=ceil(rand(populaciomeret,targyakszama)-0.5); %a populációt egy mátrixként kezeli a program a továbbiakban atlagfitnesz=zeros(generaciokszama,1); maximumfitnesz=zeros(generaciokszama,1); szkemaszam=zeros(generaciokszama,1); szkemak=szkemaepito(targyakszama); for i=1:generaciokszama %A leállási feltétel: fix generáció fut le populaciofitnesz=fitneszfv(populacio,sulyvektor,ertekvektor,sulykorlat); atlagfitnesz(i)=sum(populaciofitnesz)/populaciomeret; maximumfitnesz(i)=max(populaciofitnesz); szkemaszam(i)=szkema(populacio,szkemak); populacio=kivalaszt_rulettkerek(populacio,populaciofitnesz); populacio=keresztez_egypontos(populacio,keresztezesval); populacio=mutacio_egybit(populacio,mutacioval); end %----------------------------------------------------------------------- function populaciofitnesz=fitneszfv(populacio,sulyvektor,ertekvektor,sulykorlat) populaciofitnesz=zeros(size(populacio,1),1); %!!!preallokálás for i=1:size(populacio,1) if dot(populacio(i,:),sulyvektor)>sulykorlat populaciofitnesz(i)=dot(populacio(i,:),ertekvektor)... /(1+dot(populacio(i,:),sulyvektor)-sulykorlat); else populaciofitnesz(i)=dot(populacio(i,:),ertekvektor); end end %------------------------------------------------------------------------- function szulok=kivalaszt_rulettkerek(populacio,populaciofitnesz) %rullettkerék elven működik eloszlas=populaciofitnesz/sum(populaciofitnesz); osszegek=zeros(length(populaciofitnesz),1); osszegek(1)=eloszlas(1); for i=2:size(populaciofitnesz) osszegek(i)=osszegek(i-1)+eloszlas(i); end szulok=zeros(size(populacio,1),size(populacio,2)); for j=1:size(populacio,1) p=rand; for i=1:size(osszegek) if osszegek(i)>p break; end end szulok(j,:)=populacio(i,:); end %------------------------------------------------------------------------- function utod=keresztez_egypontos(populacio,keresztezesval) utod=populacio; n=size(populacio,2);%a kromoszómák hossza for i=1:2:size(populacio,1) if rand<keresztezesval vagopont=ceil((n-1)*rand); utod(i,:)=[populacio(i,1:vagopont), populacio(i+1,vagopont+1:n)]; utod(i+1,:)=[populacio(i+1,1:vagopont), populacio(i,vagopont+1:n)]; else utod(i,:)=populacio(i,:); utod(i+1,:)=populacio(i+1,:); end end %------------------------------------------------------------------------- function utod=mutacio_egybit(populacio,mutacioval) %random helyen lévő 1 bitet változtat %végigmegy az összes egyeden utod=populacio; for i=1:size(populacio,1) for j=1:size(populacio,2) if rand<mutacioval if populacio(i,j)==0 utod(i,j)=1; else utod(i,j)=0; end end end end %----------------------------------------------------------- function szam=szkema(populacio,szkemak) populaciomeret=size(populacio,1); targyakszama=size(populacio,2); osszesszkema=zeros(1,3^targyakszama); for i=1:populaciomeret for j=1:3^targyakszama flag=1; for k=1:targyakszama if ~(populacio(i,k)==szkemak(j,k) || szkemak(j,k)==2) flag=0; break; end end if flag==1; osszesszkema(j)=1; end end end szam=sum(osszesszkema); %--------------------------------------------------- function sz=szkemaepito(n) sz=uint8(zeros(3^n,n)); for i=2:3^n m=0; for j=1:n if sz(i-1,j)==0, sz(i,j)=1+m; sz(i,j+1:end)=sz(i-1,j+1:end); break; elseif sz(i-1,j)==1 && m==0, sz(i,j)=2; sz(i,j+1:end)=sz(i-1,j+1:end); break; elseif sz(i-1,j)==1 && m==1, sz(i,j)=0; m=1; elseif sz(i-1,j)==2 && m==0; sz(i,j)=0; m=1; elseif sz(i-1,j)==2 && m==1; sz(i,j)=1; m=1; end end end