Test problem for solving the Traveling Salesmen problem

Adjacency matrix
1. problem
Graph isomorphism
2. problem
3. problem
Brute force
Karp-Held algorithm

Adjacency matrix

The adjacency matrix of a graph (or digraph) is a 0-1 matrix. The element 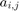$a_{i,j}$ is 1 if there is an edge between the i-th and j-th vertex, zero otherwise. If the graph is edge-weighted, then instead of the ones we write the weights.

1. problem

Let us denote the graph by G, its adjecency matrix by A.

When is A symmetric?
Prove that element (i,j) of 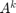is the number of routes of length k from vertex i to vertex j.
Can we prove that G is connected by investigating the powers of A?

Graph isomorphism

Let us suppose that the vertices of the graph are numbered. We call two graphs isomorphic if by permuting the vertices of the second graph, we get a graph identical to the first one.

Generally it's a hard problem to decide whether there is such a permutation. However, if we know the adjacency matrix of a graph, and have a permutation, then we can construct the adjacency matrix of the second graph. Let us suppose that we want to relabel the vertices 1,2,...,n with the permutation 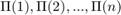$\Pi(1), \Pi(2),...,\Pi(n)$ . Let us create two 0-1 matrices. Each will contain n ones, and n^2-n zeros. In the matrix P1 there is a 1 in the k-th row and 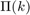$\Pi(k)$ -th column, while in matrix P2 there is a 1 in the m-th column, 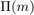$\Pi(m)$ -th row. In both matrices the other elements are zeros.

2. problem

Prove that both P1 and P2 contain exactly one 1 in each row and each column.
Prove that 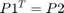and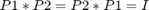
Prove that if we permute the vertices according to the permutation 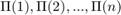$\Pi(1), \Pi(2),...,\Pi(n)$ , then the new adjacency matrix is .

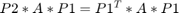3. problem

Construct you own test scalable problem for the Traveling Salesman. The following two algorithms take the adjacency matrix as an input. What is the maximum number of cities they can manage?

Brute force

function minham=tsbf(A)

n=length(A); 
p=perms(1:n);
minham=sum(sum(A));

for i=1:size(p,1)
    h=0;
    for j=1:n-1
    h=h+A(p(i,j),p(i,j+1));
    end
    h=h+A(p(i,end),p(i,1));
    if h<minham
        minham=h; 
    end
end

Karp-Held algorithm

function minham=tsdp(A)

minham=tsdpr(2:length(A),1,A);  

function y=tsdpr(S,l,A)
 
if length(S)==1 
    y=A(l,S)+A(S,1); 
else 
    lengthof=zeros(length(S),1);
     for m=1:length(S) 
        lengthof(m)=tsdpr(S([1:m-1, m+1:end]),S(m),A)+A(S(m),l);
     end
     y=min(lengthof);
end