Travelling Salesman, n-Queens
Contents
Testgraphs for the Travelling Salesman problem
tic
profofcrossover=1;
probofmutation=0.3;
numberofgen=100;
populationsize=30;
tournamentsize=5;
numberofcities=14;
numberoftrials=30;
routes_e=zeros(numberoftrials,1);
routes_i=zeros(numberoftrials,1);
routes22_e=zeros(numberoftrials,1);
routes2_i=zeros(numberoftrials,1);
routes3_e=zeros(numberoftrials,1);
routes3_i=zeros(numberoftrials,1);
for i=1:numberoftrials
[E, I]=simplecircle(numberofcities);
[E2, I2]=moderategrad(numberofcities);
[E3, I3]=notgready(numberofcities);
[m,~]=utazougynok(E,profofcrossover,probofmutation,numberofgen,populationsize, tournamentsize);
routes_e(i)=min(m);
[m,~]=utazougynok(I,profofcrossover,probofmutation,numberofgen,populationsize, tournamentsize);
routes_i(i)=min(m);
[m,~]=utazougynok(E2,profofcrossover,probofmutation,numberofgen,populationsize, tournamentsize);
routes22_e(i)=min(m);
[m,~]=utazougynok(I2,profofcrossover,probofmutation,numberofgen,populationsize, tournamentsize);
routes2_i(i)=min(m);
[m,~]=utazougynok(E3,profofcrossover,probofmutation,numberofgen,populationsize, tournamentsize);
routes3_e(i)=min(m);
[m,~]=utazougynok(I3,profofcrossover,probofmutation,numberofgen,populationsize, tournamentsize);
routes3_i(i)=min(m);
end
toc
fprintf('If the costly edges are between 4 and 7: \n')
fprintf('Found the optimum for the simple graph: %d out of: %d trials\n ', sum(routes_e==numberofcities), numberoftrials);
fprintf('Found the optimum for the isomorphic graph: %d out of: %d trials\n ', sum(routes_i==numberofcities), numberoftrials);
fprintf('If the costly edges are between 2 and 5: \n')
fprintf('Found the optimum for the simple graph: %d out of: %d trials\n ', sum(routes22_e==numberofcities), numberoftrials);
fprintf('Found the optimum for the isomorphic graph: %d out of: %d trials: %d\n ', sum(routes2_i==numberofcities), numberoftrials);
fprintf('The one the gready algorithm can''t solve \n')
fprintf('Found the optimum for the simple graph %d out of: %d trials \n ', sum(routes3_e==2*numberofcities), numberoftrials);
fprintf('Found the optimum for the isomorphic graph: %d out of: %d trials\n ', sum(routes3_i==2*numberofcities), numberoftrials);
Elapsed time is 9.080282 seconds.
If the costly edges are between 4 and 7:
Found the optimum for the simple graph: 30 out of: 30 trials
Found the optimum for the isomorphic graph: 29 out of: 30 trials
If the costly edges are between 2 and 5:
Found the optimum for the simple graph: 20 out of: 30 trials
Found the optimum for the isomorphic graph: 17 out of: 30 trials: The one the gready algorithm can't solve
Found the optimum for the simple graph 14 out of: 30 trials
Found the optimum for the isomorphic graph: 18 out of: 30 trials
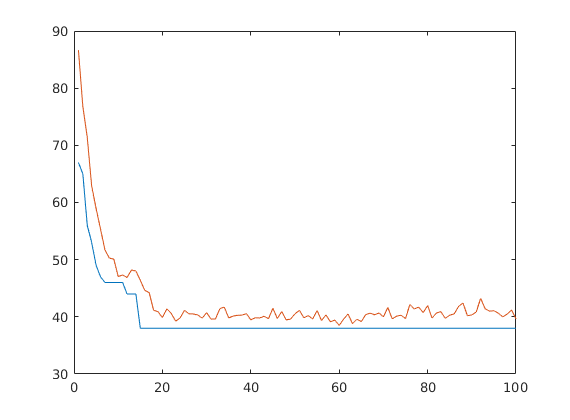
Examining the convergence
[m,a]=travsales(I3,profofcrossover,probofmutation,numberofgen,populationsize, tournamentsize);
plot(1:numberofgen, m, 1:numberofgen, a)
The testproblems
High gradient
function [ simplec, izomorphicc]=simplecircle(numberofcities)
D=randi([7 10],numberofcities);
simplec=triu(D,2)+triu(D,2)';
for j=1:numberofcities-1
simplec(j+1,j)=1;
end
for j=2:numberofcities
simplec(j-1,j)=1;
end
simplec(1,numberofcities)=1;
simplec(numberofcities,1)=1;
p=randperm(numberofcities);
permutation=zeros(numberofcities);
for j=1:numberofcities
permutation(p(j),j)=1;
end
izomorphicc=permutation'*simplec*permutation;
Low gradient
function [ simplec, isomorphicc]=moderategrad(numberofcities)
D=randi([2 5],numberofcities);
simplec=triu(D,2)+triu(D,2)';
for j=1:numberofcities-1
simplec(j+1,j)=1;
end
for j=2:numberofcities
simplec(j-1,j)=1;
end
simplec(1,numberofcities)=1;
simplec(numberofcities,1)=1;
p=randperm(numberofcities);
permutaction=zeros(numberofcities);
for j=1:numberofcities
permutaction(p(j),j)=1;
end
isomorphicc=permutaction'*simplec*permutaction;
The one the gready algoritmh can't solve
function [ simplec, izomorphicc]=notgready(numberofcities)
D=randi([6 9],numberofcities);
simplec=triu(D,2)+triu(D,2)';
for j=1:numberofcities-1
simplec(j+1,j)=2;
end
for j=1:2:numberofcities-2
simplec(j+2,j)=1;
end
for j=2:numberofcities
simplec(j-1,j)=2;
end
for j=3:2:numberofcities
simplec(j-2,j)=1;
end
simplec(1,numberofcities)=2;
simplec(numberofcities,1)=2;
p=randperm(numberofcities);
permutation=zeros(numberofcities);
for j=1:numberofcities
permutation(p(j),j)=1;
end
izomorphicc=permutation'*simplec*permutation;
The genetic algorithm
function [maxfit,meanfit]=travsales(g,pc,pm,gen,pop, tournamentmeret)
n=length(g);
population=zeros(pop,n);
for i=1:pop
population(i,:)=randperm(n);
end
meanfit=zeros(1,gen);
maxfit=zeros(1,gen);
for i=1:gen
f=fittnesz(population,g,n,pop);
meanfit(i)=mean(f);
[maxfit(i), elitpoz]=min(f);
elite=population(elitpoz,:);
population=tournament(population,f,tournamentmeret);
population=crossover(population,pc,pop);
population=mutation(population,n,pm,pop);
population(1,:)=elite;
end
function f=fittnesz(A,g,n,pop)
f=zeros(pop,1);
for i=1:pop
suly=g(A(i,n),A(i,1));
for j=1:n-1
suly=suly+g(A(i,j),A(i,j+1));
end
f(i)=suly;
end
function parents=tournament(populacio,populaciofitnesz,k)
parents=zeros(size(populacio));
for i=1:size(populacio,1)
poziciok=ceil(size(populacio,1)*rand(k,1));
[~,bestpos]=min(populaciofitnesz(poziciok));
parents(i,:)=populacio(poziciok(bestpos),:);
end
function B=crossover(A,pc,pop)
B=A;
for i=1:2:pop
if rand<pc
B(i,:) =ex(A(i,:),A(i+1,:));
B(i+1,:)=ex(A(i,:),A(i+1,:));
end
end
function A=mutation(B,n,pm,pop)
A=B;
for i=1:pop
if rand<pm
a=ceil((n-1)*rand);
b=ceil((n-1)*rand);
if a<b
vp1=a; vp2=b;
else
vp1=b; vp2=a;
end
A(i,vp1:vp2)=fliplr(B(i,vp1:vp2));
end
end
function offspring=ex(p1,p2)
n=length(p1);
edgelist=zeros(n,4);
alreadyused=zeros(n,1);
for i=1:n
if i==1
edgelist(p1(i),1)=p1(n);
edgelist(p1(i),2)=p1(2);
elseif i==n
edgelist(p1(i),1)=p1(n-1);
edgelist(p1(i),2)=p1(1);
else
edgelist(p1(i),1)=p1(i+1);
edgelist(p1(i),2)=p1(i-1);
end
if i==1
edgelist(p2(i),3)=p2(n);
edgelist(p2(i),4)=p2(2);
elseif i==n
edgelist(p2(i),3)=p2(n-1);
edgelist(p2(i),4)=p2(1);
else
edgelist(p2(i),3)=p2(i+1);
edgelist(p2(i),4)=p2(i-1);
end
end
edgelist=sort(edgelist')';
offspring=zeros(1,n);
position=randi(n);
for j=1:n
offspring(j)=position;
alreadyused(position)=1;
if sum(alreadyused)==n, return, end
edgelist(edgelist==position)=0;
if edgelist(position,1)==edgelist(position,2) && edgelist(position,1)~=0
tmp= position;
position=edgelist(position,1);
edgelist(tmp,:)=[0 0 0 0];
continue;
elseif edgelist(position,2)==edgelist(position,3) && edgelist(position,2)~=0
tmp= position;
position=edgelist(position,2);
edgelist(tmp,:)=[0 0 0 0];
continue;
elseif edgelist(position,3)==edgelist(position,4) && edgelist(position,3)~=0
tmp= position;
position=edgelist(position,3);
edgelist(tmp,:)=[0 0 0 0];
continue;
end
mlh=zeros(1,4);
for i=1:4
if edgelist(position,i)==0
mlh(i)=5;
else
mlh(i)=sum(edgelist(edgelist(position,i),:)~=0);
end
end
if sum(mlh)==20
ranpoz=randi(n);
while alreadyused(ranpoz)
ranpoz=randi(n);
end
position=ranpoz;
continue;
end
mini=min(mlh);
minipoz=(mlh==mini);
ranpoz=randi(4);
while ~minipoz(ranpoz)
ranpoz=randi(4);
end
tmp= position;
position=edgelist(position,ranpoz);
edgelist(tmp,:)=[0 0 0 0];
end
The n-queens problem
function elrendezesek=queen(n)
sor=1;
oszlop=1:n;
rossz=0;
szabad=0;
elrendezesek=0;
while 0<1
if rossz<n, oszlop(sor)=rossz+1; sor=sor+1; t=1;
elseif sor==n+1, elrendezesek=elrendezesek+1; sor=sor-1; t=oszlop(sor)+1;
elseif rossz==n, sor=sor-1; if sor==0, return, end; t=oszlop(sor)+1;
end ;
szabad=0;
for i=t:n
szabad=1;
for j=1:sor-1
if oszlop(j)==i || abs(sor-j)==abs(i-oszlop(j)), szabad=0; end
end,
if szabad==1, break, end,
end;
rossz=i-1;
szabad=0;
end,
