Continuous problems
Contents
Simple, convex test-function
x=linspace(-4,4,200); y=x; [xx,yy]=meshgrid(x,y); mesh(x,y,xx.^2+yy.^2);
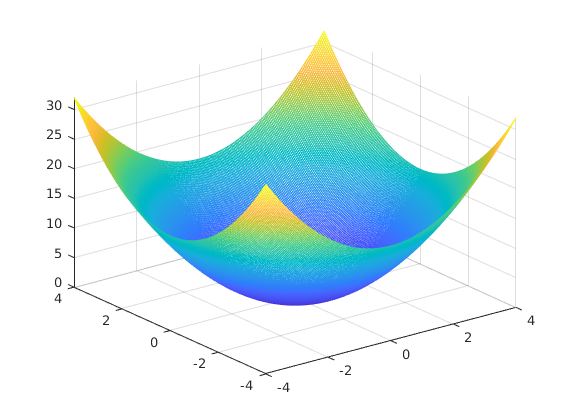
The global minimum is the origin, each algorithm can use at most 500 function evaluation.
Simulated annealing
figure(2) xMin=hutes_abra(1,1,5,2,0.2,100,@(x)x(1)^2+x(2)^2)
xMin =
0.1470
0.0608
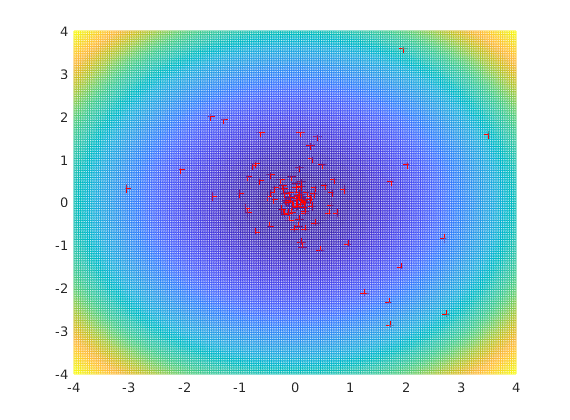
Rechenberg's algorithm
figure(3) rechenberg_abra(@(x) x(1)^2+x(2)^2,[1,1])
ans = -0.0024 -0.0123

Evolutionary strategy
figure(4) esUc1_abra(@(x) x(1)^2+x(2)^2,2)
ans =
1.0e-03 *
0.3384 -0.1276 0.6521
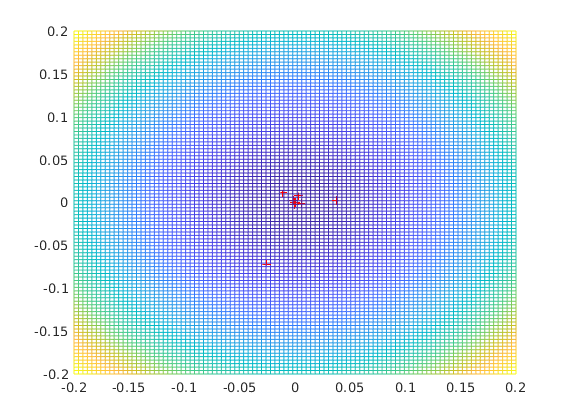
Uncorrelated Evolutionary strategy
figure(5) esUcn_abra(@(x) x(1)^2+x(2)^2,2)
ans =
0.0003 -0.0004 0.0005 0.0016

Long valley problem
figure(6) x=linspace(-4,4,200); y=x; [xx,yy]=meshgrid(x,y); mesh(x,y,10000*xx.^2+yy.^2);

It takes time the learn the directions, but might worth the effort
esUc1(@(x) 10000*x(1)^2+x(2)^2,2)
ans = -0.0006 -0.0713 0.0043
esUcn(@(x) 10000*x(1)^2+x(2)^2,2)
ans =
0.0033 0.2195 0.2027 3.0503
Recommended problem
Compare this algorithms to the gradient-method!