First practical lesson

Contents

Running time

1. problem: We measured the running time of a program for the following input sizes : 2,3,...,10 and got the following running times in seconds: 16, 39, 76, 131, 209, 312, 444, 610. Is it a polynomial algorithm? If yes, what is the exponent?

%{
 t=2:10;
 vmatlB&=[5, 16,  39, 76,  131,  209,  312, 444, 610];
 plot(log(t),log(v)), tools-> basic fitting-> linear & show equations
%}

First test-problem for backpacking:

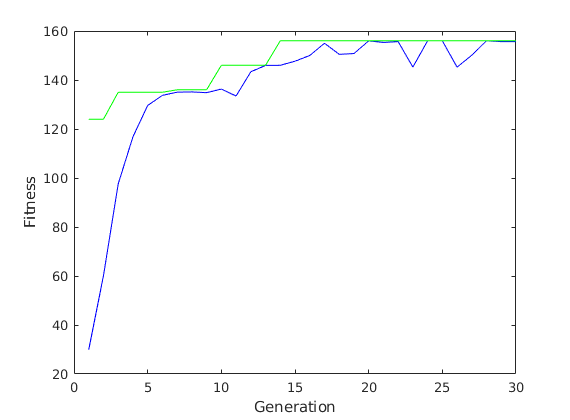
% weights:    1, 10,  1, 10,...

% Values:    10,  1, 10,  1,...

% Capacity:  the number of items multiplied by 2.5

numberofitems=30;
weights=ones(1, numberofitems);
weights(2:2:end)=10;

values=ones(1, numberofitems);
values(1:2:end)=10;

capacity=numberofitems*2.5;
% The value of optimal packing is 5.2*n (156 for 30 items)
generation=30;
populationsize=30;
probofcrossover=0.9;
probofmutation=0.05;

[fit, endpop]=hatizsak_elitista(weights,values,capacity,...
    probofcrossover, probofmutation, generation, populationsize,4);
endpop(1,:)
max(max(fit))
plot(1:generation, sum(fit)/populationsize,'b', 1:generation, max(fit,[],1),'g' )
xlabel('Generation')
ylabel('Fitness')

ans =

  Columns 1 through 13

     1     1     1     0     1     0     1     1     1     1     1     1     1

  Columns 14 through 26

     1     1     0     1     0     1     0     1     0     1     0     1     0

  Columns 27 through 30

     1     1     1     0


ans =

   156

Second test-problem

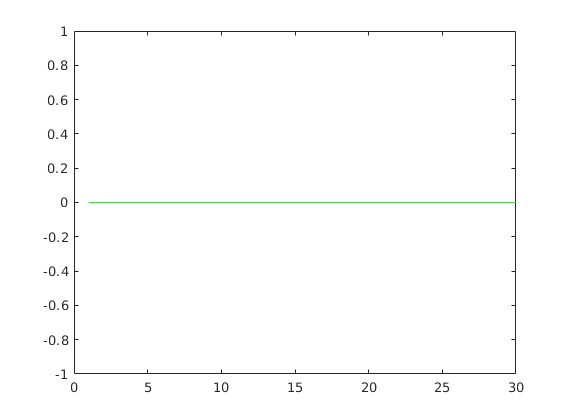
capacity=numberofitems*0.5;

[fit, endpop]=hatizsak_elitista(weights,values,capacity,...
    probofcrossover, probofmutation, generation, populationsize,4);
endpop(1,:)
max(max(fit))
plot(1:generation, sum(fit)/populationsize,'b',...
    1:generation, max(fit,[],1),'g' )

% Ideas to heal our algorithm?

ans =

  Columns 1 through 13

     0     0     0     0     1     1     0     0     1     1     1     1     0

  Columns 14 through 26

     1     0     1     0     1     0     0     0     0     1     0     0     0

  Columns 27 through 30

     0     1     0     0


ans =

     0

Statistics in Matlab

Let us suppose we change a parameter or an operator in a genetic algorithm. How can we decide, whether the performance has improved at all? The change we see can be due the the fact, that every genetic algorithm uses randomly generated numbers.

Let's see a simple example first:

a=randn(1,10); % 10 normally distributed numbers
b=randn(1,10); % the expected value is 0

Let's calculate the means

mean(a)

ans =

    0.2973

mean(b)

ans =

    0.1012

If we don't know the expected value of a probability distribution our best guess is the mean of the measurements. Now let's have 100 random numbers:

aa=randn(1,100);
bb=randn(1,100);

mean(aa)

ans =

   -0.0923

mean(bb)

ans =

    0.0471

We wish to decide, whether a and b (resp. aa and bb) has the same
expected values. In order to do this we apply two sampled t-test.

ttest2(a,b) %0 means: the t-test decided, that they expected values are the same.
% The probability of error (that is they are don't have the same expected value) is 5%.

ans =

     0

ttest2(aa,bb) % 1 wold mean, that the t-test decided, that they don't have the same expected value.

ans =

     0

Let's see how sensitive the t-test is:

a2=a-0.5;
ttest2(a2,b)

ans =

     0

a3=a-2;
ttest2(a3,b)

ans =

     1

aa2=aa-0.5;

ttest2(aa2,bb)

ans =

     1

The more data I have, the less differences becomes visible.

Source code:

function [fitn, endpop]=hatizsak_elitista(weights,values,...
    capacity,probofcrossover,probofmutation,generations,populationsize,...
    tournamentsize)


% Initial population:
numberofitems=length(weights); 
endpop=ceil(rand(populationsize,numberofitems)-0.5);  


fitn=zeros(populationsize, generations);

for i=1:generations 
    
    populaciofitness=fitness(endpop,weights,values,capacity);
    fitn(:,i)=populaciofitness;
    [~, elitpos]=max(populaciofitness);
    elitindividual=endpop(elitpos, :);
    endpop=selection_tournament(endpop,populaciofitness,tournamentsize);
    endpop=crossover_onepoint(endpop,probofcrossover);
    endpop=mutation_onebit(endpop,probofmutation);
    endpop(1,:)=elitindividual;
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function populationfitness=fitness(population,weights,values,capacity)

populationfitness=zeros(size(population,1),1); 

for i=1:size(population,1)
    
    if dot(population(i,:),weights)>capacity
        populationfitness(i)=0;
    else
        populationfitness(i)=dot(population(i,:),values);
    end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function parents=selection_tournament(population,populationfitnes,tournamentsize)

parents=zeros(size(population));

for i=1:size(population,1)
    positions=ceil(size(population,1)*rand(tournamentsize,1));
    [~,bestpos]=max(populationfitnes(positions));
    parents(i,:)=population(positions(bestpos),:);
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%


function offspring=crossover_onepoint(population,probofcrossover)

offspring=population;
n=size(population,2);

for i=1:2:size(population,1)

    if rand<probofcrossover
    
        breakpoint=ceil((n-1)*rand);
        offspring(i,:)=[population(i,1:breakpoint), population(i+1,breakpoint+1:n)];
        offspring(i+1,:)=[population(i+1,1:breakpoint), population(i,breakpoint+1:n)];
    else
        offspring(i,:)=population(i,:); 
        offspring(i+1,:)=population(i+1,:);
    end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%555

function offspring=mutation_onebit(population,probofmutation)

offspring=population;

n=size(population,2);

for i=1:size(population,1)
    if rand<probofmutation 
        position=ceil(n*rand); 
        if population(i,position)==0
            offspring(i,position)=1; 
        else
            offspring(i,position)=0;
        end
    end
end

Published with MATLAB® R2018b