Second lecture

Contents

Test problem

Weights 1, 10, 1, 10, ...

Values: 10, 1, 10, 1, ...

numberofitems=12;
weights=ones(1, numberofitems);
weights(2:2:end)=10;
values=ones(1, numberofitems);
values(1:2:end)=10;

generation=10;
populationsize=12;
probofcrossover=0.9;
probofmutation=0.03;

capacity=numberofitems*2.5; % optimal packing: 5.2*number of items
tic
[population,maxfitness,meanfitness, numberofschemes]=backpackingSchemes...
    (weights,values,capacity,probofcrossover, probofmutation, generation, populationsize);
toc

subplot(2,1,1)
plot(1:generation, numberofschemes)
ylabel('Nember of fitting schemes')
xlabel('Generation')
subplot(2,1,2)
plot(1:generation, maxfitness, 1:generation, meanfitness, 1:generation, 5.2*numberofitems*ones(1,generation))
ylabel('Fitness')
xlabel('Generation')

Elapsed time is 24.010588 seconds.

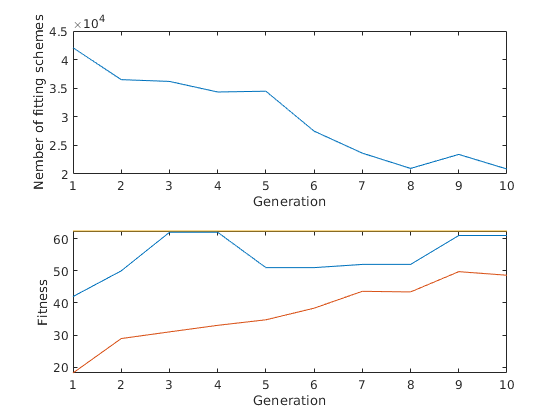
Testing and validation

The goal of testing is to optimize the parameters (and find the best fitness function). The goal of the validation is to determine whether our solution generalizes well or not.

During testing we run our algorithm on a problem whose solution is known in order to find the optimal paramaters (for example the optimal probability of mutation).

During validation test the efficiency of our solution with the optimal parameters (now fixed), parameters, to avoid the error of overestimating our solutions' effiency by fitting the parameters of our algorithm to the particular problem.

Recommended problem

How could we represent the solutions of the following problem? What could be a good test problem? How could we validate our solution?

We want to construct an error-correcting code, that is, a set of n-length 0-1 sequences. They have the property that if we select one of them (on n length word) and send it through a possibly noisy channel, then the receiver can decode our message even if there are errors in some positions. A code with minimum Hamming distance d can detect up to d - 1 errors in a code word using minimum-distance-based error-correcting.

In parcicular we have 8-long bit sequences, and we want to detect and correct if one bit is wrong. It's known that our codebook can contain at most 28 words (2^8/(8+1)).

The code for scheme counting

function [population,maxfitness,meanfitness, schemes]=backpackingSchemes(weigths,...
  values,capacity,probofcrossover,probofmutation,generations,populationsize)



numberofitems=length(weigths); 
population=ceil(rand(populationsize,numberofitems)-0.5);

meanfitness=zeros(generations,1);
maxfitness=zeros(generations,1);
schemes=zeros(generations,1);
allschemes=schemebuilder(numberofitems);

for i=1:generations 
    
    populaciofitness=fitnessfunction(population,weigths,values,capacity);
    
    meanfitness(i)=sum(populaciofitness)/populationsize;
    maxfitness(i)=max(populaciofitness);
    schemes(i)=schemescounter(population,allschemes);
    
    population=kivalaszt_roulettewheel(population,populaciofitness);
    population=x_onepoint(population,probofcrossover);
    population=mutation_bitwise(population,probofmutation);
    
    
end

%-----------------------------------------------------------------------

function populaciofitnesz=fitnessfunction(population,weigths,values,capacity)

populaciofitnesz=zeros(size(population,1),1); 

for i=1:size(population,1)
    if dot(population(i,:),weigths)>capacity
        populaciofitnesz(i)=dot(population(i,:),values)/(1+dot(population(i,:),weigths)-capacity);
    else
        populaciofitnesz(i)=dot(population(i,:),values);
    end
end

%-------------------------------------------------------------------------

function szulok=kivalaszt_roulettewheel(population,populaciofitness)


distributionoff=populaciofitness/sum(populaciofitness);
summsoff=zeros(length(populaciofitness),1);
summsoff(1)=distributionoff(1);

for i=2:size(populaciofitness)
    summsoff(i)=summsoff(i-1)+distributionoff(i);
end
szulok=zeros(size(population,1),size(population,2));
for j=1:size(population,1)    
    p=rand;
    for i=1:size(summsoff)
        if summsoff(i)>p
            break;
        end
    end
    szulok(j,:)=population(i,:);
end
    
%-------------------------------------------------------------------------

function offspring=x_onepoint(population,probofcrossover)

offspring=population;
n=size(population,2);

for i=1:2:size(population,1)

    if rand<probofcrossover
    
        cut=ceil((n-1)*rand);
        offspring(i,:)=[population(i,1:cut), population(i+1,cut+1:n)];
        offspring(i+1,:)=[population(i+1,1:cut), population(i,cut+1:n)];
    else
        offspring(i,:)=population(i,:); 
        offspring(i+1,:)=population(i+1,:);
    end
end

%-------------------------------------------------------------------------

function offspring=mutation_bitwise(population, probofmutation)

offspring=population;

for i=1:size(population,1)   
    for j=1:size(population,2)
        if rand<probofmutation
            if population(i,j)==0
                offspring(i,j)=1; 
            else
                offspring(i,j)=0;
            end
        end
    end
end

%-----------------------------------------------------------
function numberofschemes=schemescounter(populacio,schemes)

populationsize=size(populacio,1);
numberofitems=size(populacio,2);
allschemes=zeros(1,3^numberofitems);

for i=1:populationsize
    for j=1:3^numberofitems
        flag=1;
        for k=1:numberofitems
            if ~(populacio(i,k)==schemes(j,k) || schemes(j,k)==2)
                flag=0; 
                break
            end
        end
        if flag==1
            allschemes(j)=1; 
        end
    end
end

numberofschemes=sum(allschemes);


%---------------------------------------------------

function sz=schemebuilder(n)
sz=uint8(zeros(3^n,n));

for i=2:3^n
    m=0;
    for j=1:n
        if sz(i-1,j)==0         
            sz(i,j)=1+m; sz(i,j+1:end)=sz(i-1,j+1:end); 
            break 
        elseif sz(i-1,j)==1 && m==0
            sz(i,j)=2;   
            sz(i,j+1:end)=sz(i-1,j+1:end); 
            break
        elseif sz(i-1,j)==1 && m==1
            sz(i,j)=0;
            m=1;
        elseif sz(i-1,j)==2 && m==0
            sz(i,j)=0; 
            m=1;
        elseif sz(i-1,j)==2 && m==1
            sz(i,j)=1;
            m=1;
        end
    end
end


    

Published with MATLAB® R2018b