Ötödik labor: Véletlen számok, Grafika

Contents

Véletlen számok generálása

0-1 közötti véletlen (?) szám

rand

ans =

    0.8232

valójában pszeudóvéletlen

rng(0)
rand

ans =

    0.8147

egy 2*3-as mátrix

rand(2,3)

ans =

    0.9058    0.9134    0.0975
    0.1270    0.6324    0.2785

egy 1-10 közötti véletlen egész

randi(10)

ans =

     6

Hisztogram készítése

a=rand(10^5,1);
hist(a)

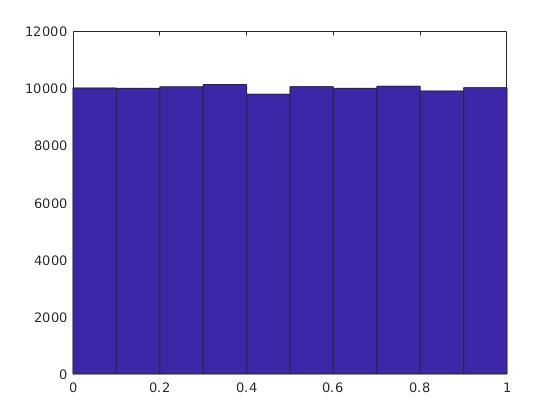
b=randn(10^5,1); % normális eloszlású valószínűségi változók
hist(b) % alapértelmezésként 10 intervallumot használ

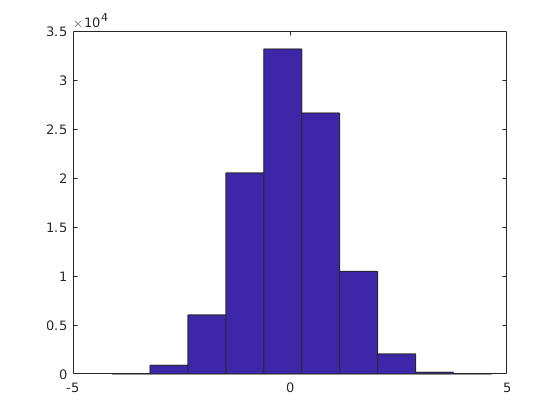
hist(b,21) % de kézzel is megadhatjuk

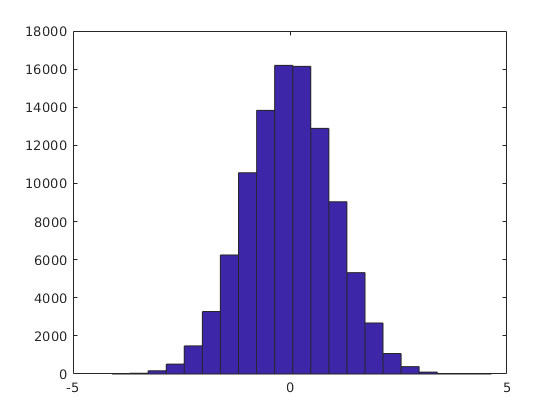
Boxplot

A változónk terjedelmét, illetve mediánját a boxplot paranccsal jeleníthetjük meg. A box alja és teteje a 25%-os ill. 75%-os percentilis, de ábrázolja a szélsőséges értékeket is.

a=rand(10, 5);
boxplot(a)

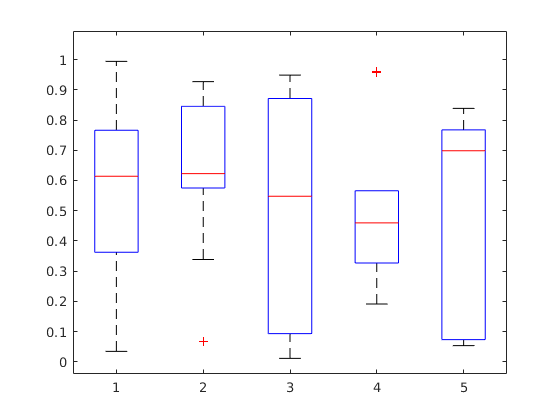
Függvények ábrázolása

ha csak egy vektor elemeit akarom ábrázolni

v=[3 5 2 5 3 1 3.4 6.2 5];
plot(v)

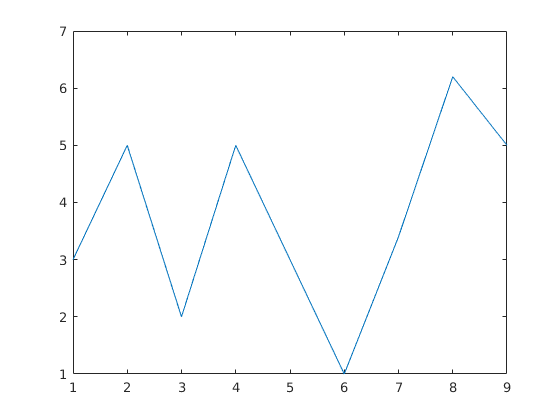
Adhatunkk stílusparancsokat is

plot(v,'ro')

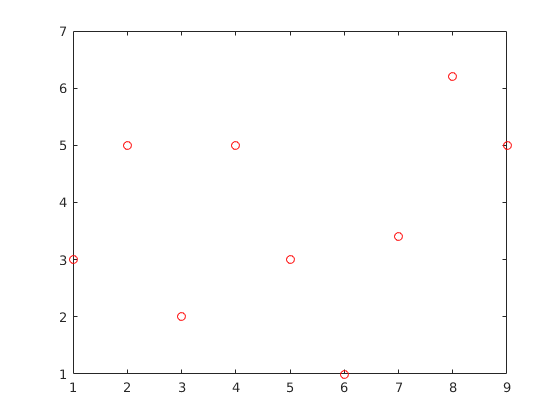
Ha egy egy függvényt, akkor elõször létrehozok egy sorvektort, ez lesz az x tengelyen:

t=linspace(0,2*pi,100);
plot(t,sin(t),'r');

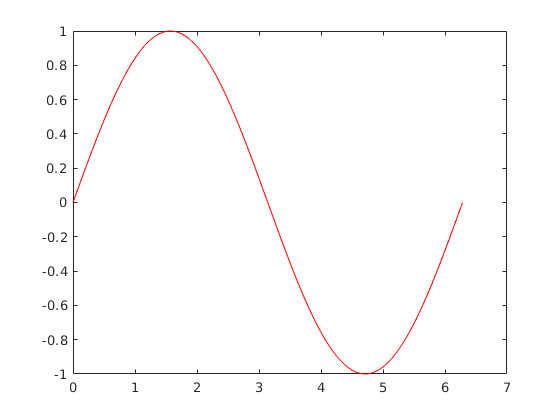
Vigyázat, bár az alábbi megoldás sem ad errort, mégis félrevezetõ (tengelyek!)

plot(sin(t));

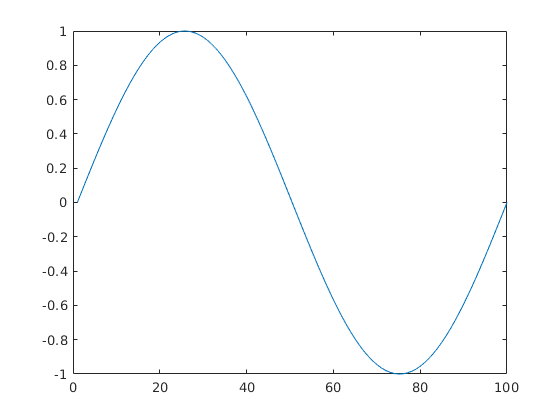
Több függvény egy ábrán

Lehet több vektor is egy plot belsejében, csak páronként kell egyforma hosszúaknak lenniük

plot(0,0,'r+',sin(t),cos(t));

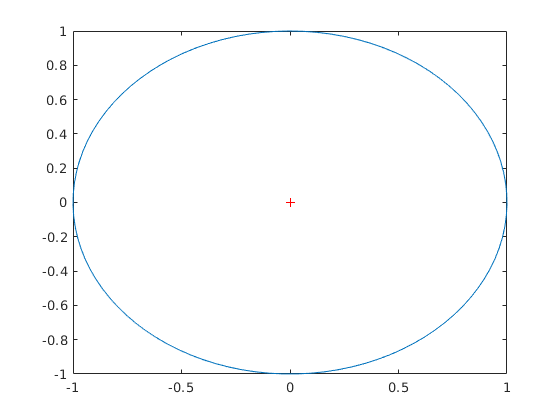
vagy: hold on parancs, akkor több különbözõ plot-ot is egy ábrára rak, például:

plot(v,'ro')
hold on
plot(t,sin(t))

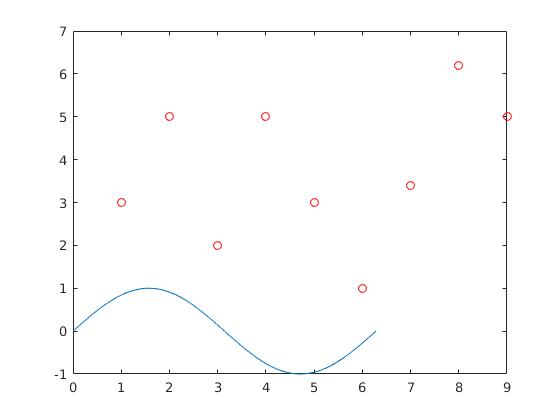
látjuk, hogy a tengelyt igazítja a legnagyobb értékekhez

hold off % ez kapcsolja ki

Paraméteres görbe kirajzolása

Ekkor nem egy függvényt ábárzolok, hanem külön megadom az x és y koordinátákat:

x=linspace(0,2*pi);
plot(cos(x),sin(x))

text(cos(x(1)),sin((x(1))), 'Kezdõpont');
xlabel('x tengely')
ylabel('y tengely')
title('Ez egy kör')
axis('equal','square')
grid on;

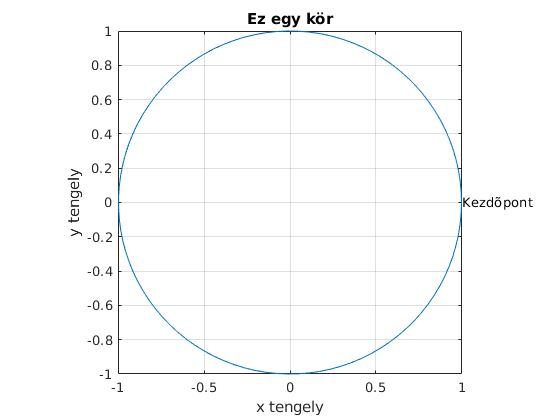
Több kép egy ábrán

t=-4:0.1:4;
subplot(2,1,1);
plot(t,sin(t))
title('A sin függvény');
subplot(2,2,3);
plot(t,cos(t))
title('A cos függvény');
subplot(2,2,4);
plot(t,exp(t))
title('Az exponenciális függvény');
hold off

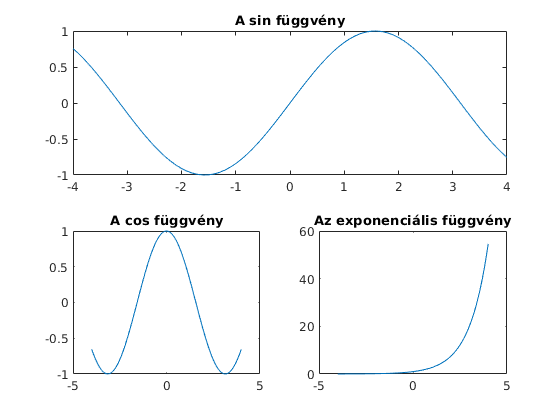
Képek importálása

A ábrán felül a File->Save As parancs segítségével, betûméretre ügyeljünk

Órai feladatok

1. feladat: Próbáljuk ki, mit történik, ha az A=rand(5) mátrixot ábrázoljuk, azaz kiadjuk a plot(A) parancsot. Keressünk magyarázatot a látottakra.

Megoldás: A mátrix elemeit oszloponként tekinti egy vektornak, és az oszloponként ábrázolja egy ábrán.

4. feladat: Írjunk egy olyan függvényt, melynek bemenete n egy pozitív egész. A függvény generáljon egy véletlen 0-1 sorozatot addig, míg az elsõ 1-es nem kapja. Jegyezze meg, hogy hanyadik kísérletre jött ki az elsõ egyes (ez lesz a kísérlet hossza). Ezt a kísérletet ismételje meg összesen n-szer. A kimenet legyen a hosszak átlaga.

function atlag=hanyadikfiu(n)
atlag=0;
for i=1:n
    szam=1;
    lany=1;
    while lany
        if rand<0.5
            lany=0;
        else
            szam=szam+1;
        end
    end
    atlag=atlag+szam;
end
atlag=atlag/n;

    

Házi feladatok

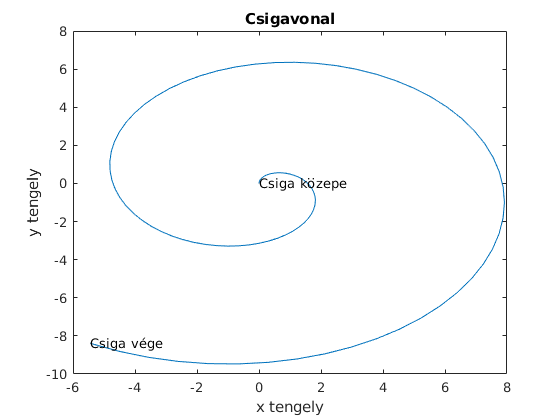
2. feladat: Ábrázoljuk az x(t)=t*cost(t), y(t)=t*sin(t) paraméteres görbét a síkon t menjen 0 és 10 között. Lássuk el az ábrát feliratokkal, majd mentsük egy .jpg fájlba.

figure(3)
t=linspace(0,10,100);
plot(t.*sin(t),t.*cos(t))
xlabel('x tengely')
ylabel('y tengely')
title('Csigavonal')
text(0,0,'Csiga közepe')
text(10*sin(10),10*cos(10),'Csiga vége')

3. feladat: Írjunk olyan függvényt, amelynek bemenete egy pozitív egész. A függvény dobjon ennyiszer egy szabályos hatoldalú dobokockával, majd kimenetként adjon vissza egy olyan hatelemû sorvektort, melynek elsõ eleme az egyesek száma, második a ketteseké, ...

function ki=dobal(n)

ki=zeros(1,6);

for i=1:n
    dobas=randi(6);
    ki(dobas)=ki(dobas)+1;
end

Published with MATLAB® R2018b