Órai feladatok megoldása

Contents

1. feladat

Próbáljuk ki, mit történik, ha az A=rand(5) mátrixot ábrázoljuk, azaz kiadjuk a plot(A) parancsot. Keressünk magyarázatot a látottakra.

A=rand(5);
plot(A)
% A mátrix elemeit oszloponként tekinti egy vektornak, és az összes oszlopot
% ábrázolja egy ábrán.

2. feladat

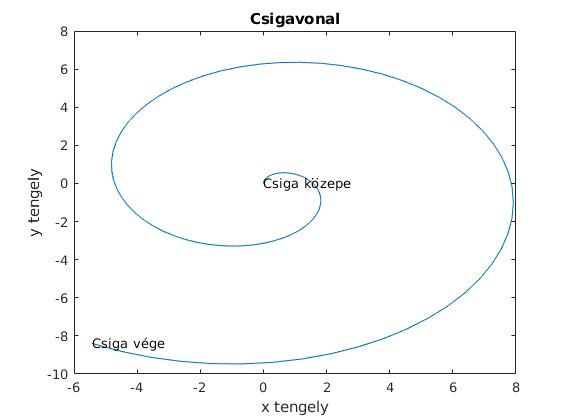
Ábrázoljuk az x(t)=t*cost(t), y(t)=t*sin(t) paraméteres görbét a síkon t menjen 0 és 10 között. Lássuk el az ábrát feliratokkal, majd mentsük egy .jpg fájlba.

t=linspace(0,10,100);
plot(t.*sin(t),t.*cos(t))
xlabel('x tengely')
ylabel('y tengely')
title('Csigavonal')
text(0,0,'Csiga közepe')
text(10*sin(10),10*cos(10),'Csiga vége')

3.feladat:

Írjunk olyan függvényt, amelynek bemenete egy pozitív egész. A függvény dobjon ennyiszer egy szabályos hatoldalú dobokockával, majd kimenetként adjon vissza egy olyan hatelemû sorvektort, melynek elsõ eleme az egyesek száma, második a ketteseké, ...

function ki=dobal(n)

ki=zeros(1,6);

for i=1:n
    dobas=randi(6);
    ki(dobas)=ki(dobas)+1;
end

4.feladat

Írjunk egy olyan függvényt, melynek bemenete n egy pozitív egész. A függvény generáljon egy véletlen 0-1 sorozatot addig, míg az elsõ 1-es nem kapja. Jegyezze meg, hogy hanyadik kísérletre jött ki az elsõ egyes (ez lesz a kísérlet hossza). Ezt a kísérletet ismételje meg összesen n-szer. A kimenet legyen a hosszak átlaga.

function atlag=hanyadikfiu(n)
atlag=0;
for i=1:n
    szam=1;
    lany=1;
    while lany
        if rand<0.5
            lany=0;
        else
            szam=szam+1;
        end
    end
    atlag=atlag+szam;
end
atlag=atlag/n;

    

Published with MATLAB® R2018a