Gyakorló óra - megoldások

1. feladat: Írjunk egy olyan milyen(v,c,d) nevű függvényt, melynek bemenete egy v oszlopvektor és két valós szám. Ha csak egy bemenettel hı́ívjuk meg a függvényt, akkor a kimenet legyen a v-ben szereplő számok maximuma, ha hárommal, akkor pedig a v vektor elemei közül a c és d számok közé eső elemeinek száma.

function ki=milyen(v,c,d)

if nargin==1
    ki=max(v);
elseif nargin==3
    ki=length(v(v>c & v<d));
else
    error('Egy vagy három bemenettel kell meghívni a függvényt.')
end

2. feladat: Adott egy xls fájl, melynek első oszlopában nevek vannak, a másodikban a születési dátumok éééé.hh.nn formátumban. Írjunk egy celkoz(s) nevű függvényt, melynek bemenete a fájl teljes neve sztringként, a kimenete pedig a 30 év feltetti emberek száma a mai napon.

function darab=celkoz(s)

[szamok, szoveg, osszes]=xlsread(s);
darab=0;

for i=1:size(osszes, 1)
    ev = str2double(szoveg{i,2}(1:4));
    ho = str2double(szoveg{i,2}(6:7));
    nap= str2double(szoveg{i,2}(9:10));
    % 2018. nov. 22-én van az óra
    if  ev< 2018-30
        darab=darab+1;
    elseif ev==2018-30 && ho < 11
        darab=darab+1;
    elseif ev==2018-30 && ho==11 && nap<=22
        darab=darab+1;
    end
end

3. feladat: Írjunk olyan feldolgoz(v) nevű függvényt, amelynek bemenete egy v cell típusú sorvektor, amely sztringként tartalmazza a mezőibe írt számokat. A függvény kimenete legyen a v vektorban szereplő pozitív számok darabszáma.

function darab=feldolgoz(v)

darab=0;

for i=1:length(v)
   szam=str2num(v{i});
   if szam>0
     darab=darab+1;
   end
end

4. feladat Tekintsük a következő szöveget:

A neuron or, also known as a neurone, is an electrically excitable cell that receives, processes, and transmits information through electrical and chemical signals. These signals between neurons occur via specialized connections called synapses. Neurons can connect to each other to form neural networks. Neurons are the primary components of the central nervous system, which includes the brain and spinal cord, and of the peripheral nervous system, which comprises the autonomic nervous system and the somatic nervous system.

Készítsük egy szt nevű változót, amely sztringkét tárolja ezt a szöveget. A Matlab segítségével határozzuk meg, hogy

a szöveg hány karakterből áll
a szöveg hány betűből áll
hány 'a' betű található a szövegben

Készítsük egy szt nevű változót, amely sztringkét tárolja ezt a szöveget.

szt='A neuron or, also known as a neurone,  is an electrically excitable cell that receives, processes, and transmits information through electrical and chemical signals. These signals between neurons occur via specialized connections called synapses. Neurons can connect to each other to form neural networks. Neurons are the primary components of the central nervous system, which includes the brain and spinal cord, and of the peripheral nervous system, which comprises the autonomic nervous system and the somatic nervous system.';

A Matlab segítségével határozzuk meg, hogy

a szöveg hány karakterből áll

karakterekszama=length(szt);
fprintf('A szöveg %d karakterből áll  \n', karakterekszama)

A szöveg 528 karakterből áll

a szöveg hány betűből áll

betukszama=0;
for i=szt
    if (double(i)>=65 && double(i)<=90) || (double(i)>=97 && double(i)<=122) % vagy egyszerűbben: isletter(i)
        betukszama=betukszama+1;
    end
end
fprintf('A szöveg %d betűből áll  \n', betukszama)

A szöveg 439 betűből áll

hány 'a' betű található a szövegben

akszama=0;
for i=szt
    if i=='a' || i=='A'
        akszama=akszama+1;
    end
end
fprintf('A szövegben %d a betű van  \n', akszama)

A szövegben 34 a betű van

5. feladat: Írjunk egy olyan legjobbParabola(v1,v2) nevű függvényt, melynek be- menetei v1 és v2 oszlopvektorok, a v1 tartalmazza a mérési pontokat, v2 a mérési értékeket. A függvény számítsa ki az ezen pontokra legkisebb négyzetes értelemben legjobban illeszkedő parabola (ax^2 +bx+c) együtthatóit, majd ábrázolja is a pontokat a parabolával együtt. A kimenet legyen a parabola három együtthatója egyetlen sorvektorban, [a, b, c] sorrendben.

function ehok=legjobbParabola(v1,v2)

ehok=polyfit(v1,v2,2);

t=linspace(min(v1)-1, max(v1)+1);
plot(v1,v2, 'r+', t, polyval(ehok,t));
legend('Pontok', 'Illesztett parabola');

6. feladat: Tegyük fel, hogy megmértük egy ismeretlen háttérfüggvényből származó mennyiség értékeit a [0; 2; 3; 6; 9; 11.4; 16; 20] pontokban, és rendre a [0.8147; 3.5058; 4.0270; 8.7134; 12.3324; 14.9175; 21.0785; 26.5469] értékeket kapuk. Ábrázoljuk a mért értékeket, ez alapján válaszoljuk meg, hogy reális feltevés-e, hogy az összefüggés lineáris? Ha igen, akkor keressük meg a mérési eredményekhez a legkisebb négyzetes értelemben legjobban illeszkedő egyenest, és ábrázoljuk is a pontokkal együtt!

meresipont=[0; 2; 3; 6; 9; 11.4; 16; 20];
mertertek =[0.8147; 3.5058; 4.0270; 8.7134; 12.3324; 14.9175; 21.0785; 26.5469] ;

plot(meresipont, mertertek, 'r+')

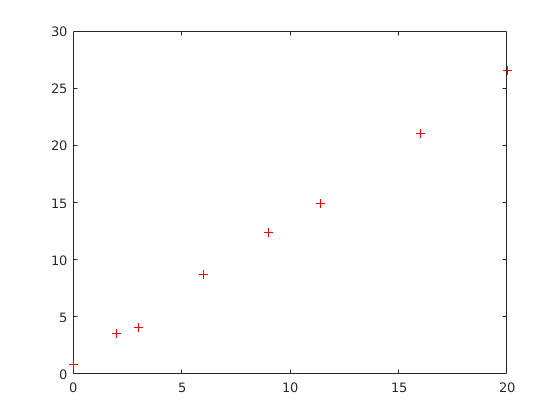
Ez alapján reálisnak látszik lineáris összefüggést feltenni.

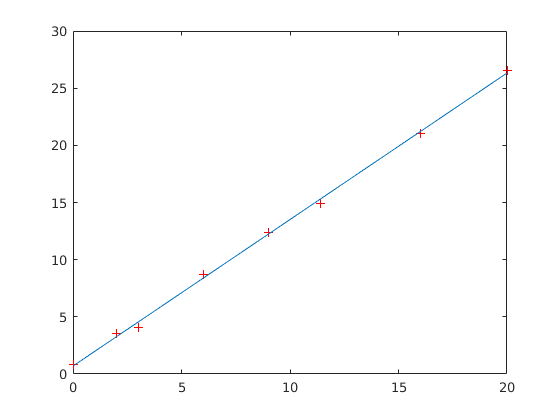
egyutthatok=polyfit(meresipont, mertertek, 1)
abrazolasitartomany=linspace(0,20);
kozelitoertek=polyval(egyutthatok, abrazolasitartomany);
plot(meresipont, mertertek, 'r+', abrazolasitartomany, kozelitoertek)

egyutthatok =

    1.2813    0.6967