Elsó pótzárthelyi megoldásai

1. feladat: Írjunk egy olyan helyesAtlag(v) nevű függvényt, amelynek bemenete egy valós számokat tartalmazó sorvektor, kimenetei pedig v 0 és 10 közé eső értékű elemeinek darabszáma és átlaga.

function [db,atlag]=helyesAtlag(v)

db=lenght(v(v>0 & v<10));
atlag=mean(v(v>0 & v<10));

2. feladat: Írjunk egy olyan legnagyobbElem(A) nevű függvényt, amelynek bemenete A egy mátrix, kimenete pedig az első elem abból a sorból, amelyben legnagyobb az adott sorban lévő elemek összege.

function ki=legnagyobbElem(A)

sorosszegek=sum(A,2);
[ln, in]=max(sorosszegek);
ki=A(in,1);

3. feladat: Írjunk egy olyan nemfibbSor(n) nevű függvényt, melynek a bemenete egy n pozitív egész, és a kimenete az f_{n}=f_{n-1}+2f_{n-2}, f_1=1, f_2=1 rekurzióval adott sorozat n-edik eleme.

function ki=nemfibbSor(n)

if n==1
    ki=1;
elseif n==2
    ki=1;
else
    tegnap=1;
    tegnapelott=1;
    for i=3:n
        ki=tegnap+2*tegnapelott;
        tegnapelott=tegnap;
        tegnap=ki;
    end
end

4. feladat: Írjunk egy olyan penzFeldobas nevű függvényt, amely meghívásakor elkezd dobálni egy szabályos pénzérmét (1/2 esélye van a mindkét különböző kimenetnek). Addig dobáljon, amíg öt fej egymás után ki nem jön. A kimenet legyen az ehhez szükséges dobások száma.

function dobasokszama=penzFeldobas

fejekszama=0;
dobasokszama=0;
while fejekszama<5
    dobas=ceil(rand-0.5); % 0 ha fej, 1 ha írás 
    dobasokszama=dobasokszama+1;
    if dobas==0
        fejekszama=fejekszama+1;
    else 
        fejekszama=0;
    end
end

5. feladat: Írjunk egy olyan abrafv(a,b) nevű függvényt, amelynek bemenete a<b valós számok. A függvény egy ábrára egymás mellé rajzolja ki a sin(x) és a tan(3x), függvényeket az a,b intervallumon. Az ábráról derüljön ki, hogy melyik vonal melyik függvényhez tartozik. A függvénynek ne legyen kimenete.

function abrafv(a,b)
t=linspace(a,b);
subplot(1,2,1)
plot(t, sin(t))
title('sin(x) függvény')
subplot(1,2,2)
plot(t, tan(3*t))
title('tan(3x) függvény')

Szorgalmi feladat: Írjunk egy olyan reciprokOsszeg(n) nevű függvényt, amelynek kimenete a legkisebb olyan k pozitív egész, melyre az 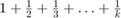$1+\frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{k}$ összeg nagyobb, mint a bemenetként kapott n szám. Ha egymilliónál is több tag kellene, akkor a kimenet legyen -1.

function ki=reciprokOsszeg(n)

ki=1;
osszeg=1;
while osszeg<=n
    ki=ki+1;
    if ki>1e6
        ki=-1;
        return
    end
    osszeg=osszeg+1/ki;
end