Negyedik labor

Contents

Jacobi iteráció

Kirajzolja a k. lépésben a hibavektor normájának logaritmusát is

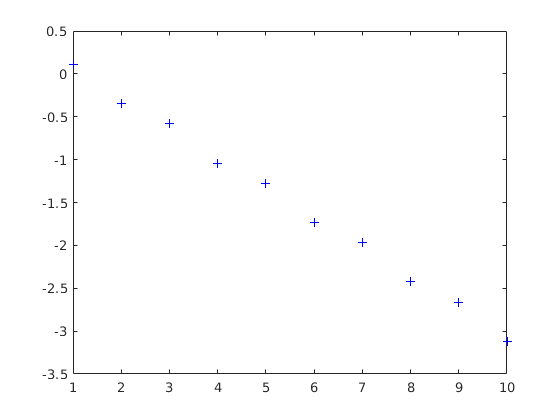
function JacobiIt(A,b)
D=diag(diag(A));
L=tril(A,-1);
U=triu(A,1);
B=-inv(D)*(L+U);
f=inv(D)*b;
x=zeros(size(b));
if det(D)==0 
    error('Nem létezik D inverze!');
end
maradekok=zeros(10,1);

for k=1:10
    x=B*x+f;
    maradekok(k)=norm(b-A*x);
end
rho=max(abs(eig(B)));
fprintf('A spektrálsugár logaritmusa: %4.2f\n',log(rho));
figure(1)
plot(log(maradekok),'b+')

Használata:

A=[2 -1; -1 1]; b=[1;1]; JacobiIt(A,b)

A spektrálsugár logaritmusa: -0.35

Relaxált változat

function x=JacobiIt2(A,b,omega)
D=diag(diag(A));
U=triu(A,1);
L=tril(A,-1);
if det(D)==0
    error('Van a főátlóban 0')
end
B=eye(size(A))*(1-omega)-omega*inv(D)*(L+U);
f=omega*inv(D)*b;
xpontos=linsolve(A,b);
x=zeros(size(b));
for k=1:10
    x=B*x+f;
    maradek(k)=norm(x-xpontos);
end
rho=max(abs(eig(B)));
fprintf('A spektrálsugár logaritmusa: %4.2f\n',log(rho));
figure(2)
plot(1:10, log(maradek),'r+')


JacobiIt2(A,b,0.5)

A spektrálsugár logaritmusa: -0.16

ans =

    1.5770
    2.4018

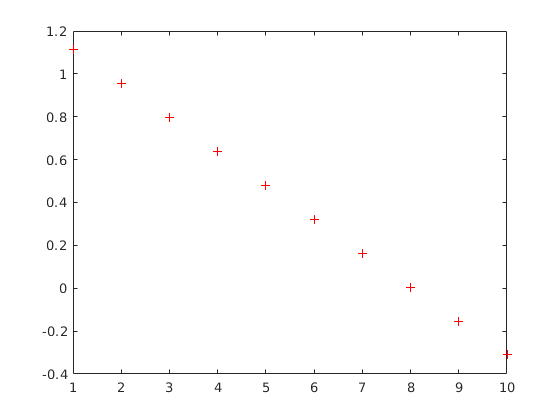
Látjuk, hogy csökkent a konvergencia sebessége.

Gradiensmódszer

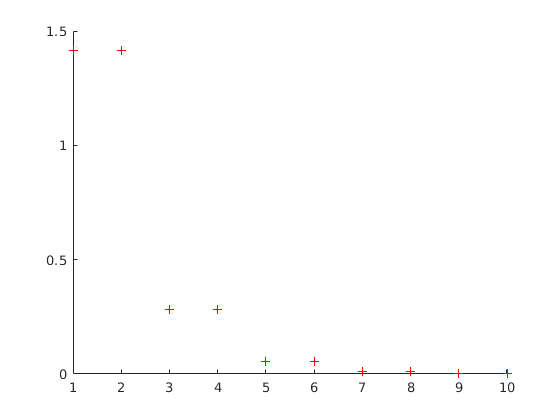
function x=gradiensM(A,b)

x=zeros(size(b));
figure(3) %új ablakot nyit az ábrázolásnak
hold on
for i=1:10
    maradek=b-A*x;
    lepestavolsag=(maradek'*maradek)/(maradek'*A*maradek);
    x=x+lepestavolsag*maradek;
    plot(i,norm(maradek),'r+');
end
hold off

Használata:

gradiensM(A,b)

ans =

    1.9994
    2.9990

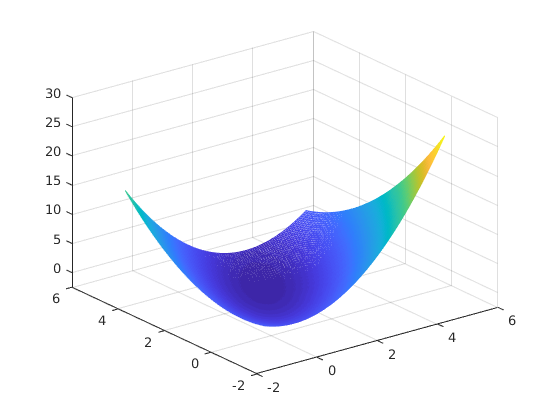
A 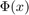$\Phi(x)$ függvény felülete:

x1=linspace(-1,5);
y1=x1;
[x2, y2]=meshgrid(x1,y1); % rács létrehozása!
z=1/2*(A(1,1)*x2.^2+2*A(1,2)*x2.*y2+A(2,2)*y2.^2)-b(1)*x2-b(2)*y2; % felület magassága a rács felett
figure(4) % új ablak az ábrának
mesh(x1,y1,z) % ábra elkészítése


Published with MATLAB® R2018a