Numerikus integrálás
Contents
Trapézformula
A közelítő integrált kiszámító függvény:
function kvadr=trapez(a,b,n,fv)
h=(b-a)/n;
x=(a+h):h:(b-h);
kvadr=h*sum(fv(x))+h*fv(a)/2+h*fv(b)/2;
A Matlab beépített intergálófüggvénye a integral(), ezzel ellenőrizhetjük a konvergencia sebességét. Legyen a függvény f(x)=x*sin(x), ezt egy külön fájlba mentjük fv.m néven. Ekkor:
for i=1:4 trapez(1,2,10^i,@fv)-integral(@fv,1,2) end
ans = -0.0011 ans = -1.0873e-05 ans = -1.0873e-07 ans = -1.0873e-09
A hiba jól láthatóan O(h^2), hiszen egy lépsében 1/10-edére vetten az osztásközt, ettől a hiba kb 1/100-adára változott.
Simpson formula
Órai feladat: Valósítsuk meg Matlabban a Simpson-kvadratúrát!
function kvadr=simpsonkv(a,b,n,fv)
h=(b-a)/n;
x=a+h : h: b-h;
x2=a+h/2 : h : b-h/2;
kvadr=h*(2/6*sum(fv(x))+4/6*sum(fv(x2))+fv(a)/6+fv(b)/6);
Innen:
for i=1:4 simpsonkv(1,2,10^i,@fv)-integral(@fv,1,2) end
ans =
4.0605e-08
ans =
4.0594e-12
ans =
0
ans =
0
A hiba O(h^4). Persze létezik jobb, ha a 3-adfokú (4-edfokú,...) Lagrange-interpolációs polinommal közelítünk.
Romberg-módszer
A másik lehetőség a Romberg-módszer használata. Ehhez:
trapez(1,2,10,@fv)-integral(@fv,1,2) trapez(1,2,20,@fv)-integral(@fv,1,2)
ans = -0.0011 ans = -2.7184e-04
Ezekre Romberg
(4*trapez(1,2,20,@fv)-trapez(1,2,10,@fv))/3-integral(@fv,1,2)
ans = 4.0605e-08
Ami ugyanaz mint a Simpson
simpsonkv(1,2,10,@fv)-integral(@fv,1,2)
ans = 4.0605e-08
Differenciálegyenletek megoldása
A definíció egy külön .m fájlban:
function dy=myode1(t,y)
dy=1-10*y;
Utána a megoldó. Ez egy adaptív lépésközű, negyedrendű, ötödrendűben beágyazott egylépéses Runge-Kutta módszert valósít meg
[T,Y]=ode45(@myode1,[0,0.5],0);
A megoldó szerint a megoldás 0.5-ben:
y12=Y(end); fprintf('Abszolút hiba: %d\n',(y12-1/10*(1-exp(-5)))); fprintf('Relatív hiba: %d\n',(y12-1/10*(1-exp(-5)))/(1/10*(1-exp(-5))));
Abszolút hiba: -5.805908e-08 Relatív hiba: -5.845294e-07
beallitasok=odeset('AbsTol', 1e-10); [T,Y]=ode45(@myode1,[0,0.5],0,beallitasok); y12=Y(end); fprintf('Abszolút hiba: %d\n',(y12-1/10*(1-exp(-5)))/(1-exp(-5))); fprintf('Relatív hiba: %d\n',(y12-1/10*(1-exp(-5)))/(1/10*(1-exp(-5))));
Abszolút hiba: -6.053078e-08 Relatív hiba: -6.053078e-07
beallitasok=odeset('MaxStep',1e-3); [T,Y]=ode45(@myode1,[0,0.5],0,beallitasok); y12=Y(end); fprintf('Abszolút hiba: %d\n',(y12-1/10*(1-exp(-5)))/(1-exp(-5))); fprintf('Relatív hiba: %d\n',(y12-1/10*(1-exp(-5)))/(1/10*(1-exp(-5))));
Abszolút hiba: -5.588772e-17 Relatív hiba: -5.588772e-16
Paraméterek átadása. Most a külön .m fájban megadott differenciálegyenletnek bemenete a paraméter.
function dy=myode2(t,y,a)
dy=3*y-a;
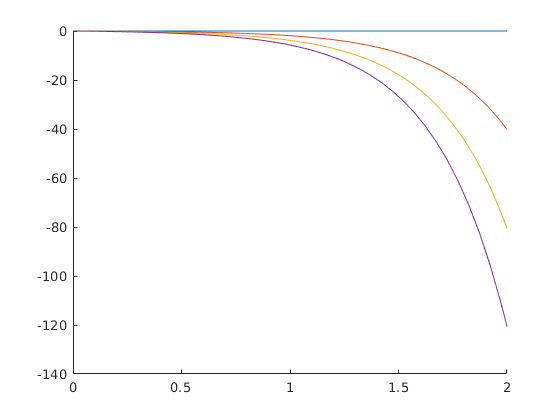
A megoldó használata:
hold on for a=0:0.3:1 [T,Y]=ode45(@(t,y)myode2(t,y,a),[0,2],0); plot(T,Y) end