KDE-k megoldása Matlabban

Contents

Egyismeretlenes elsőrendű közönséges differenciálegyenlet

Malthus-féle növekedési modell

Jelöljük a t időpillanatban egy faj egyedeinek számát N(t)-vel. Ekkor N'(t) jelöli a változás sebességet. Ha korlátlan mennyiségben áll rendelkezésre tápanyag, akkor N'(t) egyenesen arányos az adott pillanatban jelenlévő egyedek számával, azaz a differenciálegyenlet: N'(t)=rN(t), ahol r>0 arányossági tényező. Ezen differenciálegyenletet szeretnénk megoldani Matlabban.

function dy=malthus(t,y)
dy=0.3*y;

Az általános megoldó az ode45, ennek használatához szükségünk van a külön fájlban lévő differenciálegyenletre, egy kezdeti feltételre, és egy időintervallumra, amin meg szeretnénk oldani a differenciálegyenletet.

[T,Y]=ode45(@malthus,[0,20],1);

Ekkor ábrázolva a megoldást:

plot(T,Y)

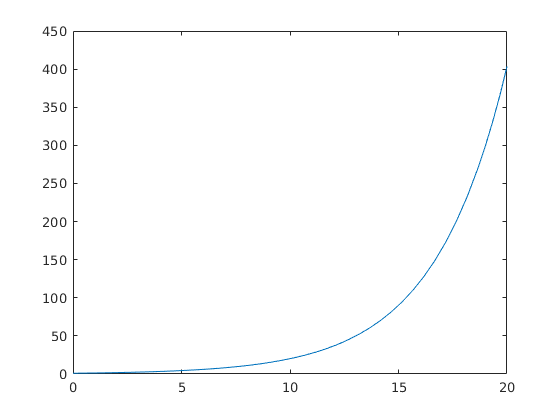
Látjuk, hogy egy egyedből 20 időegység alatt több mint 400 lett. Ez történik például sáskajáráskor.

Paraméterek megadása

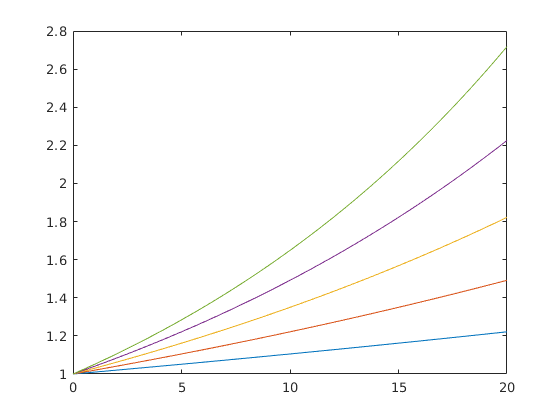
Ha a paramétert nem a differenciálegyenlet belsejében szeretnénk megadni (mert például különböző paraméterértékekre is meg szeretnénk oldani az egyenletet), akkor a function handle-t tudjuk használni. Most úgy írjuk fel a függvényt, hogy a paramétertől is függ:

function dy=malthus2(t,y,r)
dy=r*y;

A malthus2 -ben leírt differenciálegyenletet megoldva:

for i=1:5
    r=i/100;
    [T,Y]=ode45(@(t,y)malthus2(t,y,r),[0,20],1);
    plot(T,Y)
    hold on
end
hold off

Verlust-féle logisztikus modell

A Malthus-féle modell nem veszi figyelembe a környezet fenntartó képességét. Ezt például úgy vehetjük figyelembe, a növekedés üteme nem konstans lesz, hanem ha a környezet fenntartó képességét K-val jelöljük, akkor a növekedés üteme rN(t)(1-N(t)/K)-val lesz arányos (azaz ha N(t)>K, akkor negatív, így csökken az egyedszám). Ekkor:

function dy=verlust(t,y)
dy=0.3*y.*(1-y/10);

A megoldás:

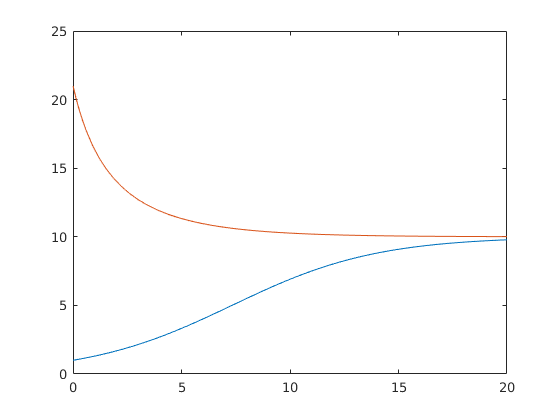
[T,Y]=ode45(@verlust,[0,20],1);
plot(T,Y)

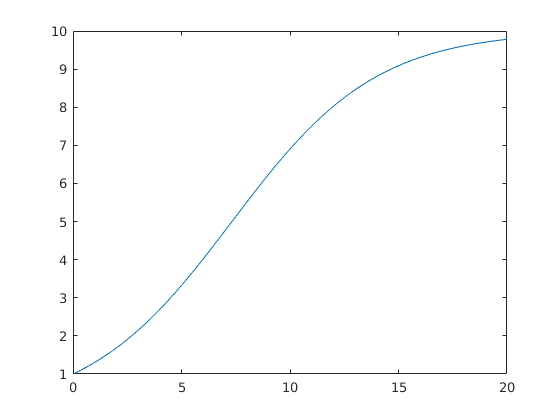
Ez is érdekes:

[T2,Y2]=ode45(@verlust,[0,20],21);
hold on
plot(T2,Y2);
hold off

Többismeretlenes elsőrendű közönséges differenciálegyenletrendszer

Kétfajos Lotka-Volterra ragadozó-zsákmány modell

Tegyük fel, hogy két faj él együtt: egy növényevő és egy ragadozó. Szeretnénk az ő kapcsolatukat modellezni. Növényevő önnmagában egy Verlust-típusú modell szerint növelkedne, azaz N(t)-vel jelölve az egyedszámot: N'(t)=r(1-N(t)/K)N(t) viszont ha jelen van egy ragadozó faj is (jelölje P(t) az ő elemszámát): N'(t)=r(1-N(t)/K)N(t)-a*N(t)*P(t) itt alfa az méri, hogy mennyire hatékony ragadozó P. Az általa elejtett zsákmány mennyisége arányos továbbá azzal, hogy mennyi zsákmányállat van jelen, illetve azzal, hogy mennyi ragadozó van jelen. A ragadozó száma zsákmányállat nélkül csökkenne (mert éhenhalnának), de az elejtett zsákmányállatok egy részét gyarapodásra fordítják, így az ő egyenletük: P'(t)=-bP(t)+cN(t)P(t) Ezen egyenletrendszer szeretnénk megoldani Matlabban. Ehhez:

function dy = lotvol(t,y)
r=0.5;
K=2;
a=0.1;
b=0.3;
c=0.5;

dy = [ r*(1-y(1)/K)*y(1)-a*y(1)*y(2); -b*y(2)+c*y(1)*y(2)];

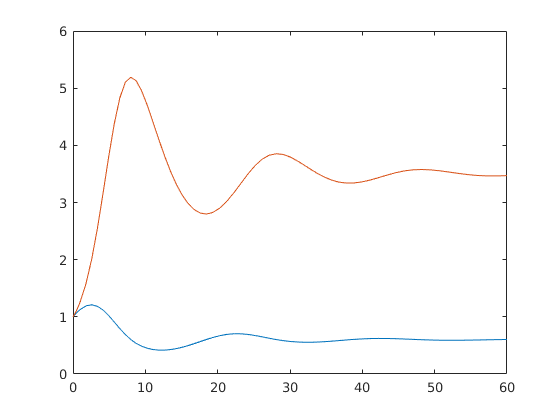
Most a megoldáshoz 2 kezdeti feltételre van szükség:

[T,Y]=ode45(@lotvol,[0,60],[1,1]);
plot(T, Y(:,1),T, Y(:,2))

Fázisportré

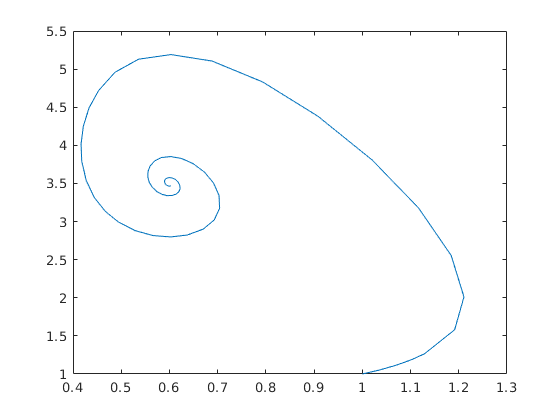
Kirajzolhatjuk a fázisportrét is, azaz, hogy hogyan alakul az állatok száma egymáshoz képest:

plot(Y(:,1),Y(:,2))

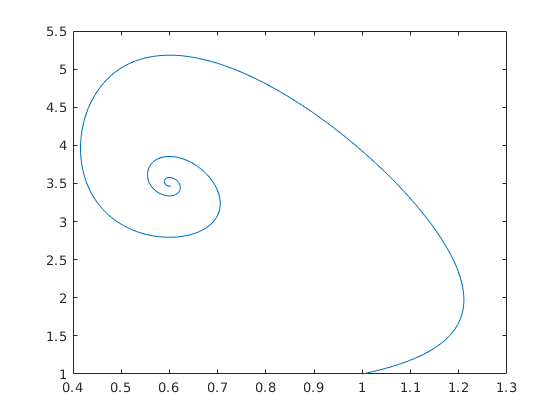
Számítási pontosság

Láthatjuk, hogy a fázisportrén a megoldások ábrája már 'darabos', töröttvonal-szerű. A számítási pontosság növelésével kisimíthatjuk az ábrát, azaz pontossabban közelíthetjük a megoldást. Az alapértelmezett hiba 10^-6 a relatív és az abszolút hibára is.

beallitasok = odeset('RelTol',1e-10,'AbsTol',1e-10);
[T3,Y3]=ode45(@lotvol,[0,60],[1,1],beallitasok);
plot(Y3(:,1),Y3(:,2))

Egyensúlyi helyzetek típusai

Azt is megfigyelhetjük, hogy a megoldások viselkedése nem függ attól, hogy a 0 időpillanatban milyen egyedsűrűségekből indult a rendszer

[T ,Y ]=ode45(@lotvol,[0,60],[1,1],beallitasok);
[T2,Y2]=ode45(@lotvol,[0,60],[2,1],beallitasok);
[T3,Y3]=ode45(@lotvol,[0,60],[1,2],beallitasok);
plot(Y(:,1),Y(:,2), Y2(:,1),Y2(:,2), Y3(:,1),Y3(:,2) )

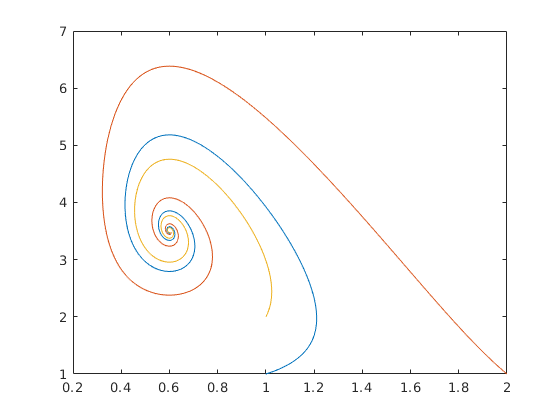
Linearizálással bebizonyíthatjuk, hogy az egyensúlyi helyezet asziptótikusan stabil fókusz, amely azonban csak bizonyos paraméter értékeknél helyezkedik el a pozitív negyedsíkban.

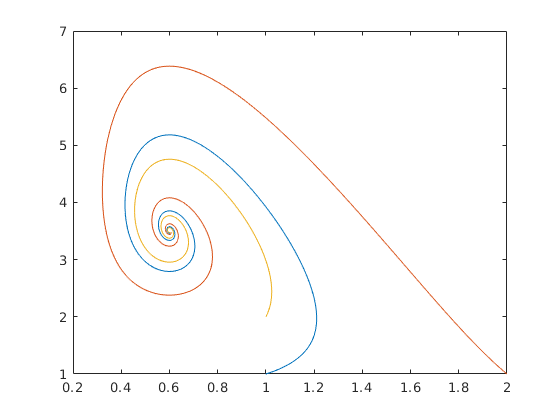
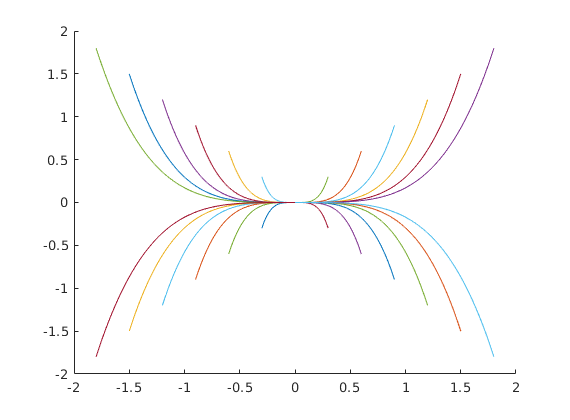
A fókuszon kívűl egy kétdimenziós rendszer egyensúlyi helyzete lehet még csomó:

function dy=csomo(t,y)

dy=[-y(1); -4*y(2)];

figure
hold on
for i=0:0.3:2
[T,Y]=ode45(@csomo,[0,60],  [i,i],beallitasok);
plot(Y(:,1),Y(:,2) )
[T2,Y2]=ode45(@csomo,[0,60],  [-i,i],beallitasok);
plot(Y2(:,1),Y2(:,2) )
[T4,Y4]=ode45(@csomo,[0,60],  [i,-i],beallitasok);
plot(Y4(:,1),Y4(:,2) )
[T5,Y5]=ode45(@csomo,[0,60],  [-i,-i],beallitasok);
plot(Y5(:,1),Y5(:,2) )
end
hold off

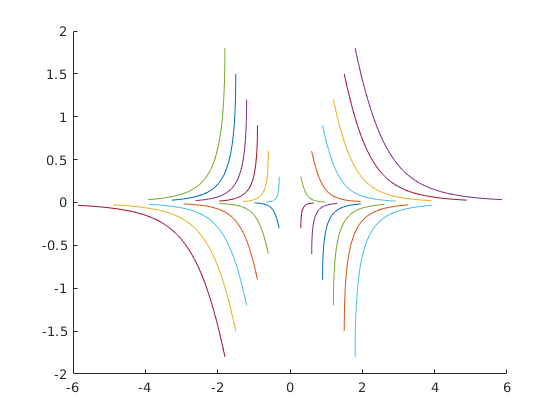
illetve nyereg

function dy=nyereg(t,y)

dy=[y(1)+y(2); -4*y(2)];

figure
hold on
for i=0:0.3:2
[T,Y]=ode45(@nyereg,[0,1],  [i,i],beallitasok);
plot(Y(:,1),Y(:,2) )
[T2,Y2]=ode45(@nyereg,[0,1],  [-i,i],beallitasok);
plot(Y2(:,1),Y2(:,2) )
[T4,Y4]=ode45(@nyereg,[0,1],  [i,-i],beallitasok);
plot(Y4(:,1),Y4(:,2) )
[T5,Y5]=ode45(@nyereg,[0,1],  [-i,-i],beallitasok);
plot(Y5(:,1),Y5(:,2) )
end
hold off

Másodrendű közönséges differenciálegyenlet megoldása

Kőhajítás

Tegyük fel, hogy eldobunk egy követ függőlegesen felfelé, jelöljük a kő magasságát t időpontban y(t)-vel. Ekkor hat rá a gravitáció, ami gyorsulást okoz lefelé irányba. Ez azt jelenti, hogy függőleges irányban a gyorsulása: -g (ami nagyjából 9.8 m/s^2). Ekkor a differenciálegyenlet y''(t)=-9.8 lesz. A Matlab azonban csak elsőrendű differenciálegyenleteket tud kezelni, ezért át kell alakítanunk egy elsőrendű rendszerré. Legyen v(t) a kő sebessége a t időpontban. Ekkor y'(t)=v(t), illetve v'(t)=-9.8 (mert a sebesség deriváltja a gyorsulás); azaz vektorosan összefoglalva a helyzetet (első koordináta) és a sebességet (második koordináta):

 function dyv = ko(t,yv)
 %yv(1), a magasság: y(t)
 %yv(2) a függőleges sebesség: v(t)
 dyv = [yv(2); -9.8]; %fontos, hogy oszlopvektorként adjuk meg

Legyen a kezdősebesség 20 m/s, és a földről indul, azaz 0 magasságról, így a megoldó az első 10 másodpercre

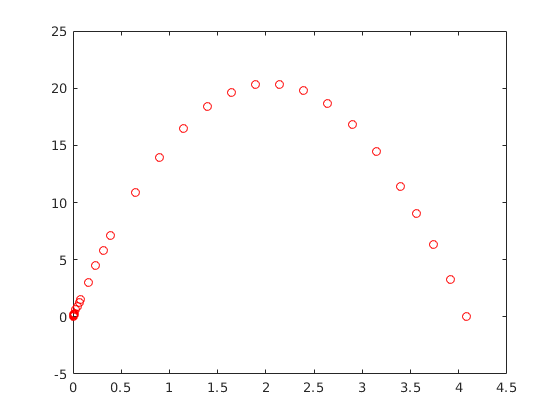
[T3,Y3]=ode45(@ko, [0, 10],[0,20]);
plot(T3,Y3(:,1), 'rO', T3,Y3(:,2),'b')

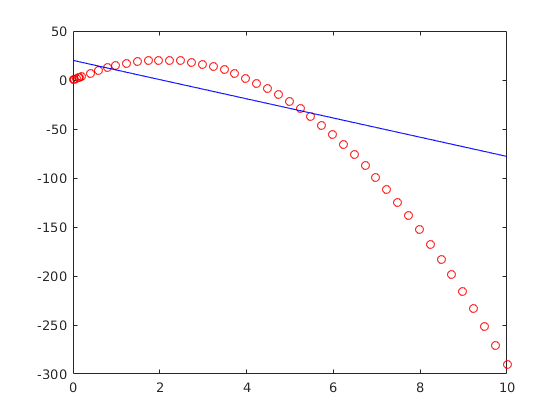
Láthatjuk, hogy a magasság negatív a végén. Ennek nincs értelme, hiszen a kő elvben nem mehet a föld alá, ezért meg kell állítani a megoldót, amikor eléri a 0 magasságot. Ehhez esemény-detektálásra van szükség, azaz kell készíteni egy esemény függvényt:

function [ertek,megalle,irany] = esemeny(t,y)

ertek = y(1);     
megalle = 1;   
irany = 0;   

% Ennek használatához a megoldónak át kell adni az eseményt detektáló
% függvényt, amelyet az odeset parancson keresztül tehetünk meg.

beallitasok = odeset('Events',@esemeny,'RelTol', 10^-6);
[T4,Y4] = ode45(@ko,[0 10],[0,20],beallitasok);
plot(T4,Y4(:,1), 'rO')

% Itt amikor 0 lett a magasság, nem számol tovább. A T4 vektorban összegyűjti,
% hogy mely pontban számolta ki (közelítette) a megoldást. T4 utolsó eleme
% az, amikor megállt a megoldó

T4(end)

% ebből láthatjuk, hogy kb 4 másodperc alatt esett vissza a földre a kő.

ans =

    4.0816

Published with MATLAB® R2018b