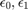Első labor: A lebegőpontos számítások alapjai

Contents

Túlcsordulás

A Matlab dupla pontosságú lebegőpontos ábrázolásában 52 bit jut a mantisszára (értékes jegyek száma), 1 előjelbit, 11 jegy a karakterisztikára (de ebből egy előjelbit). Ennek következménye:

(2^53+1)-2^53

ans =

     0

$\epsilon_0, \epsilon_1$

A legkisebb ábrázolható szám: 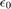$\epsilon_0$

realmin

ans =

    2.225073858507201e-308

Viszont ez nem azt jelenti, hogy ilyen finomsággal tudjuk ábrázolni a lebegőpontos számokat. Ezt az 1 utáni legkisebb ábrázolható szám adja meg: 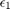$\epsilon_1$

format long
1+2^-52

ans =

   1.000000000000000


1+2^-53

ans =

     1


53/10*3

ans =

  15.899999999999999

Ez nagyjából 15 értékes jegynek felel meg, ennyi a maximális szóbajövő számítási pontosság. Sajnos ez sem mindig elérhető.

Összeadás

s=1;
p=0;
for i=1:10
    s=s+10^(-16);
    p=p+10^(-16);
end
s

s =

     1


p=p+1

p =

   1.000000000000001

Azaz érdemes először a kicsi tagokat összeadni, nem mindegy a sorrend.

Kivonás

Vegyük a két elvben egyforma mennyiséget: sqrt(a)-sqrt(a-1), illetve 1/(sqrt(a)+sqrt(a-1)).

c=sqrt(10^6)-sqrt(999999)

c =

     5.000001250436981e-04


d=1/(sqrt(10^6)+sqrt(999999))

d =

     5.000001250000625e-04

Kiegyszerűsödés: két közeli szám kivonasákor fellépő jegyveszteség Ha a két számban az első k jegy azonos, akkor a különbségükben az első k jegy értektelen Az elsőben az utolsó 6 jegy nem stimmel, a második a jó. Tanulság: numerikusan megbízhatatlan egymáshoz közeli számok kivonása.

Vegyük az x^2+b*x+1 egyenlet gyökeit. Ekkor a diszkrimináns: sqrt(b^2-4*a*c), azaz

b=10^9; %esetén
D=sqrt(b^2-4) % a diszkrimináns

D =

     1.000000000000000e+09

Ekkor az egyik gyök: (-b+D)/2, itt:

x1=(-b+D)/2 % ez rossz, viszont helyette az előbbi módszerrel

x1 =

     0


x11=-2/(b+D) % ami sokkal közelebb van a pontos gyökhöz (bár nem annyi)

x11 =

    -1.000000000000000e-09

Szorzás

Sajnos itt sem számíthatunk pontos eredményre minden szituációban:

(1-10^-9)*(1+10^-9)

ans =

     1

A nagy számmal való szorzás is veszélyes művelet, ugyanis felnagyíthatja a hibákat.

Osztás

A 0 közeli számokkal veszélyes osztani, például:

1/(sqrt(10^10)-sqrt(10^10-1))

ans =

     2.000002233314028e+05

helyette:

sqrt(10^10)+sqrt(10^10-1)

ans =

     1.999999999950000e+05

Saját függvények

Mi magunk is készíthetünk saját függvényeket, a már beépített függvények felhasználásával. Ennek módja function kimenet(ek)=függvénynév(bemenet(ek)) ez egy külön .m fájlba kell menteni, hogy mûködjön, és a fájl nevén kell meghívni.

A függvényüket a parancssorból tudjuk használni, ha abban a könyvtárban vagyunk, ahová mentettük. Ezt a pwd paraccsal (vagy a felsõ sorban) ellenõrizhetjük.

Vigyázat, minden a függvény belsejében szereplõ változó lokális, azaz a függvény futása után nem tudjuk elérni, például v-t sem látjuk!

Több bemenet és kimenet is lehetséges, ez a függvény például visszaadja a bementeként kapott számok összegét és szorzatát

function [osszeg, szorzat]=szamol(a,b)

osszeg=a+b;
szorzat=a*b;

Példa

Készítsünk egy olyan függvényt, amely minél pontosabban oldja meg a másodfokú egyenletet (vizsgálja, hogy lehet-e kiegyszerűsödés). Az első sor legyen function [gyok1, gyok2]=masodfoku(a,b,c).

function [gyok1, gyok2]=masodfoku(a,b,c)
% Thf nem hiányos, azaz a~=0, b~=0, c~=0
D=sqrt(b^2-4*a*c);

if b>0
    gyok1=-2*c/(b+D);
    gyok2=(-b-D)/(2*a);
elseif b<0
    gyok1=(-b+D)/(2*a);
    gyok2=(-2*c)/(b-D);
end

Sorösszegek

Példa: Ismert, hogy 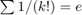$\sum 1/(k!)=e$. Adjuk össze az első 17 tagot az eredeti és a fordított sorrendben is! Melyik a pontosabb?

s=0;
for i=0:17
    s=s+1/factorial(i);
    fprintf('A %d-k lépés hibája %d\n',i,s-exp(1))
end

s2=0;
for i=17:-1:0
    s2=s2+1/factorial(i);
end
fprintf('A fordított sorrendű összeadásnál %d a hiba a 17. lépésben\n',s2-exp(1))
fprintf('Az e konstans Matlab szerinti értéke: %2.17f\n',exp(1))
fprintf('                  a pontos érték: e = 2.71828182845904523536028747135…\n')
fprintf('                    A mi s becslésünk %2.17f\n',s)
fprintf('                   A mi s2 becslésünk %2.17f\n',s2)

A 0-k lépés hibája -1.718282e+00
A 1-k lépés hibája -7.182818e-01
A 2-k lépés hibája -2.182818e-01
A 3-k lépés hibája -5.161516e-02
A 4-k lépés hibája -9.948495e-03
A 5-k lépés hibája -1.615162e-03
A 6-k lépés hibája -2.262729e-04
A 7-k lépés hibája -2.786021e-05
A 8-k lépés hibája -3.058618e-06
A 9-k lépés hibája -3.028859e-07
A 10-k lépés hibája -2.731266e-08
A 11-k lépés hibája -2.260553e-09
A 12-k lépés hibája -1.728768e-10
A 13-k lépés hibája -1.228617e-11
A 14-k lépés hibája -8.153478e-13
A 15-k lépés hibája -5.062617e-14
A 16-k lépés hibája -2.664535e-15
A 17-k lépés hibája 0
A fordított sorrendű összeadásnál -4.440892e-16 a hiba a 17. lépésben
Az e konstans Matlab szerinti értéke: 2.71828182845904553
                  a pontos érték: e = 2.71828182845904523536028747135…
                    A mi s becslésünk 2.71828182845904553
                   A mi s2 becslésünk 2.71828182845904509


Published with MATLAB® R2018b