Második labor: vektornormák és indukált mátrixnormák
Contents
Vektorok és mátrixok létrehozása
Elemenként: szögletes zárójelben a sorvektort, az elemek közé , vagy semmi.
v=[1 2 4];
;-el elválasztva az oszlopvektort:
w=[5 ; 6 ; -1]
w =
5
6
-1
Mátrixok esetén a sorok közé ; kell, a mátrix voltaképpen egy (sor)vektorokból álló (oszlop)vektor
C=[1 0 3; 4 3 -1; 3 -5 8]
C =
1 0 3
4 3 -1
3 -5 8
itt az 1 0 3 az első sor,
Vagy lehet előre definiált függvényekkel:
Olyan mátrix aminek diagonálisa (főátlója) a bemenetként kapott vektor
A=diag(v)
A =
1 0 0
0 2 0
0 0 4
5*5-os egység mátrix
I=eye(5)
I =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
csupa 0-t tartalmazó 5*2-os mátrix
Z=zeros(5,2)
Z =
0 0
0 0
0 0
0 0
0 0
csupa egyet
E=ones(2,3)
E =
1 1 1
1 1 1
a mátrix mérete
size(C)
ans =
3 3
sorainak száma
size(E,1)
ans =
2
oszlopainak a száma
size(E,2)
ans =
3
a sorainak és oszlopainak száma közül a nagyobb (vektor esetén a hossz)
length(E)
ans =
3
Számokból álló sorvektor létrehozására használhatjuk a : operátort a:b:c módon. Első szám: kezdőérték, második szám: lépésköz, harmadik szám végpont (pontosabban az az érték amit a végpont nem haladhat meg). Például:
x=0:0.3:1
x =
0 0.3000 0.6000 0.9000
Ez egy sorvektor
whos
Name Size Bytes Class Attributes A 3x3 72 double C 3x3 72 double E 2x3 48 double I 5x5 200 double Z 5x2 80 double ans 1x1 8 double v 1x3 24 double w 3x1 24 double x 1x4 32 double
Másik lehetőség sorvektor létrehozására: egyenlő osztásközű sorvektor, a harmadik számnyi elemmel
y_sor=linspace(1,2,5)
y_sor =
1.0000 1.2500 1.5000 1.7500 2.0000
Vigyázat a Matlab megkülönbözteti a sor- és oszlopvektorokat!
Indexelés
A sorvektor egyes elemeit a () segítségével indexelhetjük, a sorszámozás 1-el kezdődik
x(1)
x(2)
% de x(6)!
ans =
0
ans =
0.3000
értékadásnál nagyon oda kell figyelnünk, mert:
x(6)=5
x =
0 0.3000 0.6000 0.9000 0 5.0000
sőt
x2(12)=5
x2 =
0 0 0 0 0 0 0 0 0 0 0 5
egy konkrét elem lekérdezése (3. sor 2. oszlop)
C(3,2)
ans =
-5
oszlopfolytonosan számítva a 6. elem
C(6)
ans =
-5
Első sor lekérése
C(1,:)
ans =
1 0 3
ez itt a felső 2*2-es mátrix
C(1:2,1:2)
ans =
1 0
4 3
Ez pedig C minden második oszlopa
C(:,1:2:3)
ans =
1 3
4 -1
3 8
Norma és kondíciószám
A vektorok p normáját a norm paracs segítségével kérdezhetjük le
norm(x)
norm(x,2)
norm(x,1)
norm(x,'inf')
ans =
5.1245
ans =
5.1245
ans =
6.8000
ans =
5
az indukált mátrixnormát szintén a norm parancs adja meg
norm(C) norm(C,2) norm(C,1) norm(C,'inf') norm(C,'fro')
ans =
10.3412
ans =
10.3412
ans =
12
ans =
16
ans =
11.5758
a kondíciószámot pedig a cond parancs
cond(C) cond(3*C)
ans =
7.9188
ans =
7.9188
cond(C,1) cond(C',1)
ans = 14.6471 ans = 11.5294
Sajátértékek
A mátrix sajátértéket egyetlen vektorban az eig parancs segítségével kaphatjuk meg
eig(A)
ans =
1
2
4
a sajáértékek lekérdezéséhez két kimenetettel hívjuk meg az eig függvényt:
[se,sv]=eig(A)
se =
1 0 0
0 1 0
0 0 1
sv =
1 0 0
0 2 0
0 0 4
ekkor a spektálfelbontását is elkészíthetjük a mátrixnak
sv*se*inv(sv)
ans =
1 0 0
0 1 0
0 0 1
Gersgorin körök
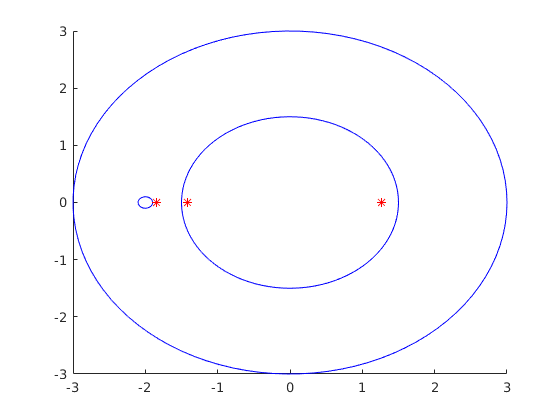
Az alábbi függvények kirajzolja a mátrix Gersgorin-köreit és mellé a sajátértékeket is:
function gerg1(C) hold on % Rárajzol az előző ábrára for i=1:size(C,1) kozeppont=C(i,i); sugar=sum(abs(C(i,:)))-abs(kozeppont); t=linspace(0,2*pi); plot(sugar*cos(t)+real(kozeppont), sugar*sin(t)+imag(kozeppont),'b'); % Körök kirajzolása kék színnel end sajatert=eig(C); plot(real(sajatert),imag(sajatert),'r*'); % sajátértékek piros *-al
Használatával mutathatunk példát olyan mátrixra, amelynek van üres köre:
C=[0 0.5 1; 3 0 0; 0 0.1 -2] gerg1(C)
C =
0 0.5000 1.0000
3.0000 0 0
0 0.1000 -2.0000