Hatodik labor

Contents

Gyökkereső eljárások

Intervallumfelezés

function gyok=felezo(f,a,b,lepes)
% Függvény használata: felezo(f,a,b,lepes) ahol f egy egyváltozós függvény, 
% amelyre az [a,b] intervallumon teljesül, hogy f(a)f(b)<0. 
% Meghívásakor a függvény lepes darab iterációt végez.
if f(a)*f(b)>0
    error('Nem megfelelő kezdőintervallum')
    elseif f(a)==0
    gyok=a;
    return
elseif f(b)==0
    gyok=b;
    return
end

c=a+(b-a)/2;
for i=1:lepes
    if f(c)==0
        gyok=c;
        return
    elseif f(c)*f(a)<0
        b=c;
    else
        a=c;
    end
    c=a+(b-a)/2;
end
gyok=c;

Példa az eljárás használatára:

gyok1=felezo(@sin,3,4, 10)

gyok1 =

   3.141113281250000

pi-gyok1

ans =

     4.793723397931160e-04

Newton-módszer

function gyok=newtonIt(f,df,x0,lepes)
% Függvény használata: newtonIt(f,df,x0) ahol f egy egyváltozós függvény, 
% df pedig a deriváltja.
% Meghívásakor a függvény lepes darab iterációt végez.
gyok=x0;
for i=1:lepes
    gyok=gyok-f(gyok)/df(gyok);
end
    

Példa az eljárás használatára:

gyok2=newtonIt(@sin,@cos,3,10)

gyok2 =

   3.141592653589793

pi-gyok2

ans =

     0

A hibabecsléshez:

for i=1:10
    gyok1=felezo(@sin,3,4, i);
    gyok2=newtonIt(@sin,@cos,3,i);
    fprintf('Az %d-edik lépésben a hiba intervallumfelezéssel: %d, Newton-módszerrel: %d \n',i, gyok1-pi, gyok2-pi)
end

Az 1-edik lépésben a hiba intervallumfelezéssel: 1.084073e-01, Newton-módszerrel: 9.538895e-04 
Az 2-edik lépésben a hiba intervallumfelezéssel: -1.659265e-02, Newton-módszerrel: -2.893161e-10 
Az 3-edik lépésben a hiba intervallumfelezéssel: 4.590735e-02, Newton-módszerrel: 0 
Az 4-edik lépésben a hiba intervallumfelezéssel: 1.465735e-02, Newton-módszerrel: 0 
Az 5-edik lépésben a hiba intervallumfelezéssel: -9.676536e-04, Newton-módszerrel: 0 
Az 6-edik lépésben a hiba intervallumfelezéssel: 6.844846e-03, Newton-módszerrel: 0 
Az 7-edik lépésben a hiba intervallumfelezéssel: 2.938596e-03, Newton-módszerrel: 0 
Az 8-edik lépésben a hiba intervallumfelezéssel: 9.854714e-04, Newton-módszerrel: 0 
Az 9-edik lépésben a hiba intervallumfelezéssel: 8.908910e-06, Newton-módszerrel: 0 
Az 10-edik lépésben a hiba intervallumfelezéssel: -4.793723e-04, Newton-módszerrel: 0 

Órai feladat

Próbáljuk ki az x^3+3x^2-4 függvény gyökeinek keresésére az x0=-3 pontból indítva a Newton-módszert. Mi történt?

Megoldás

for i=1:10
    gyok=newtonIt(@(x)x^3+3*x^2-4,@(x)3*x^2+6*x,-3,i);
    fprintf('Az %d-edik lépésben a közelítés hibája: %d \n',i,gyok+2)
end

Az 1-edik lépésben a közelítés hibája: -5.555556e-01 
Az 2-edik lépésben a közelítés hibája: -2.979066e-01 
Az 3-edik lépésben a közelítés hibája: -1.553902e-01 
Az 4-edik lépésben a közelítés hibája: -7.956221e-02 
Az 5-edik lépésben a közelítés hibája: -4.028844e-02 
Az 6-edik lépésben a közelítés hibája: -2.027681e-02 
Az 7-edik lépésben a közelítés hibája: -1.017232e-02 
Az 8-edik lépésben a közelítés hibája: -5.094741e-03 
Az 9-edik lépésben a közelítés hibája: -2.549528e-03 
Az 10-edik lépésben a közelítés hibája: -1.275305e-03 

Látjuk, hogy jóval lassabb a konvergencia négyzetesnél. Ennek oka, hogy a -2 többszörös gyök, ami például az alábbi ábrából is kiderül:

t=linspace(-3,2);
plot(t,t.^3+3*t.^2-4,t, zeros(size(t)))

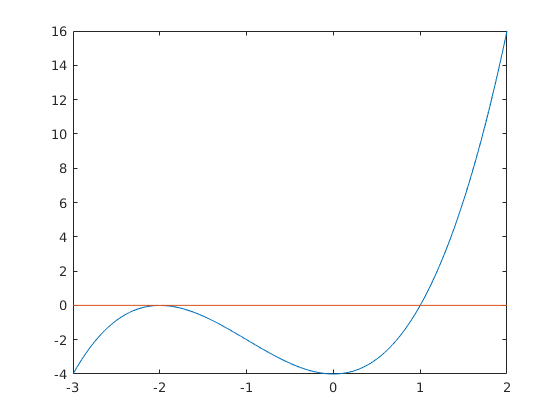
Ennek megfelelően az 1 közelében tényleg négyzetes a konvergencia

for i=1:10
    gyok=newtonIt(@(x)x^3+3*x^2-4,@(x)3*x^2+6*x,0.5,i);
    fprintf('Az %d-edik lépésben a közelítés hibája: %d \n',i,gyok-1)
end

Az 1-edik lépésben a közelítés hibája: 3.333333e-01 
Az 2-edik lépésben a közelítés hibája: 5.555556e-02 
Az 3-edik lépésben a közelítés hibája: 1.949318e-03 
Az 4-edik lépésben a közelítés hibája: 2.528298e-06 
Az 5-edik lépésben a közelítés hibája: 4.261480e-12 
Az 6-edik lépésben a közelítés hibája: 0 
Az 7-edik lépésben a közelítés hibája: 0 
Az 8-edik lépésben a közelítés hibája: 0 
Az 9-edik lépésben a közelítés hibája: 0 
Az 10-edik lépésben a közelítés hibája: 0 

Published with MATLAB® R2018b