Hetedik labor: Fixpont kereső iterációk
Contents
format long
Feladat
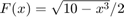 -vel indított
-vel indított 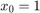 ,
, 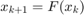 iterációról ismert, hogy konvergens és a
iterációról ismert, hogy konvergens és a 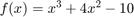 függvény egyetlen gyökéhez tart. Az is ismert, hogy az F(x) kontrakció q=0.66-os konstanssal. Ábrázoljuk a hibabecslést és a valódi eltérést az iteráció folyamán. Pontos-e a becslés legalább aszimptótikusan?
függvény egyetlen gyökéhez tart. Az is ismert, hogy az F(x) kontrakció q=0.66-os konstanssal. Ábrázoljuk a hibabecslést és a valódi eltérést az iteráció folyamán. Pontos-e a becslés legalább aszimptótikusan?
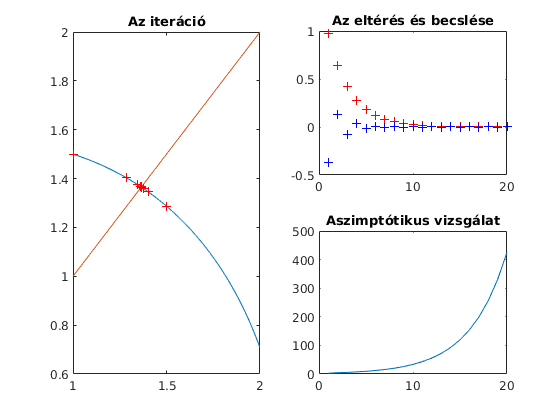
t=linspace(1,2); subplot(1,2,1) plot(t, sqrt(10-t.^3)/2,t,t) title('Az iteráció') gyok=newtonIt(@(x)x^3+4*x^2-10,@(x)3*x^2+8*x,1,11) % A Newton-iteráció a múlt órán szerepelt x=1; hold on for i=1:20 subplot(1,2,1) plot(x,sqrt(10-x^3)/2, 'r+') becsles(i)=0.66^i/(1-0.66)*0.5; valodi(i)=x-gyok; fprintf('Az %d-ik lépésben az eltérés: %d\n',i, x-gyok) x=sqrt(10-x^3)/2; end hold off subplot(2,2,2) plot(1:20,becsles,'r+', 1:20,valodi,'b+') title('Az eltérés és becslése') subplot(2,2,4) plot(1:20,abs(becsles./valodi)) title('Aszimptótikus vizsgálat')
gyok = 1.365230013414097 Az 1-ik lépésben az eltérés: -3.652300e-01 Az 2-ik lépésben az eltérés: 1.347700e-01 Az 3-ik lépésben az eltérés: -7.827625e-02 Az 4-ik lépésben az eltérés: 3.731079e-02 Az 5-ik lépésben az eltérés: -1.977164e-02 Az 6-ik lépésben az eltérés: 9.940239e-03 Az 7-ik lépésben az eltérés: -5.135821e-03 Az 8-ik lépésben az eltérés: 2.616954e-03 Az 9-ik lépésben az eltérés: -1.343010e-03 Az 10-ik lépésben az eltérés: 6.867200e-04 Az 11-ik lépésben az eltérés: -3.517962e-04 Az 12-ik lépésben az eltérés: 1.800478e-04 Az 13-ik lépésben az eltérés: -9.219274e-05 Az 14-ik lépésben az eltérés: 4.719511e-05 Az 15-ik lépésben az eltérés: -2.416312e-05 Az 16-ik lépésben az eltérés: 1.237030e-05 Az 17-ik lépésben az eltérés: -6.333189e-06 Az 18-ik lépésben az eltérés: 3.242328e-06 Az 19-ik lépésben az eltérés: -1.659951e-06 Az 20-ik lépésben az eltérés: 8.498295e-07