Nyolcadik labor: Interpoláció

Contents

Lagrange-interpoláció

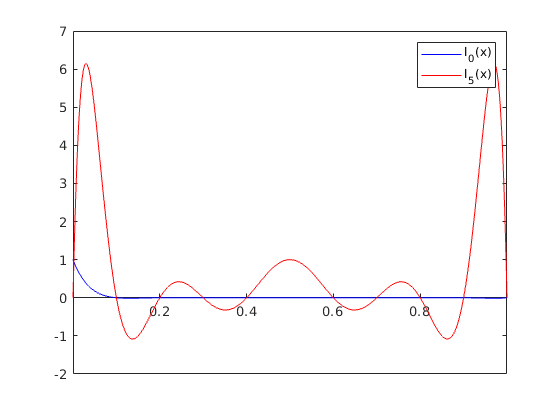
Ábrázoljuk a [0,1] intervallumon 11 ekvidisztans alaponthoz tartozó alappolinomok közül l_0(x)-et és l_5(x)-et!

t=linspace(0,1,1e3);
alappont=0:0.1:1;
l0=1;
for i=2:11
    l0=l0.*(t-alappont(i))./(alappont(1)-alappont(i));
end
l5=1;
for i=[1:5 7:11]
    l5=l5.*(t-alappont(i))./(alappont(6)-alappont(i));
end
plot(t, l0,'b',t,l5,'r'); legend('l_0(x)', 'l_5(x)'),
ax=gca; ax.XAxisLocation = 'origin';

Órai feladat ábrázoljuk az f(x)=1/(1+x^2) függvényt és az f(x)-et a [-5,5] intervallumon 11 ill. 21 ekvidisztans alapponton interpoláló polinomot. Segítség: nézzük meg a polyfit paracsot! Oldjuk meg ugyanezen feladatot Csebisev-alappontokkal.

Megoldás

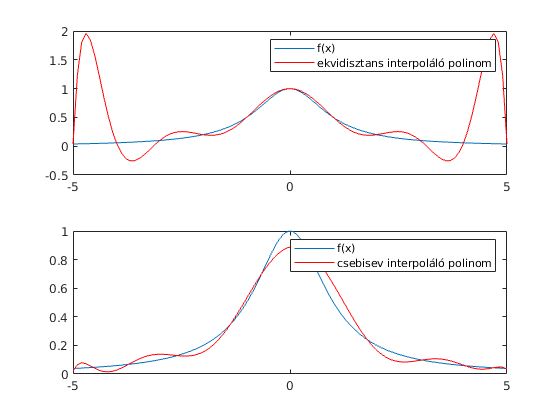
function rungellcsebi(n)

% Ekivdisztans alapontrsz
x1=-5:10/(n-1):5;
f1=1./(1+x1.^2);
eho1=polyfit(x1,f1,n-1);

% Csebisev alappontrsz
x2=5*cos((2*(0:n)+1)/(2*n+1)*pi);
f=1./(1+x2.^2);
eho2=polyfit(x2,f,n-1);

%% Ábra
t=linspace(-5,5);
subplot(2,1,1)
plot(t,1./(1+t.^2),t,polyval(eho1,t),'r');
legend('f(x)', 'ekvidisztans interpoláló polinom'), 
subplot(2,1,2)
plot(t,1./(1+t.^2),t,polyval(eho2,t),'r');
legend('f(x)', 'csebisev interpoláló polinom'), 

rungellcsebi(11)

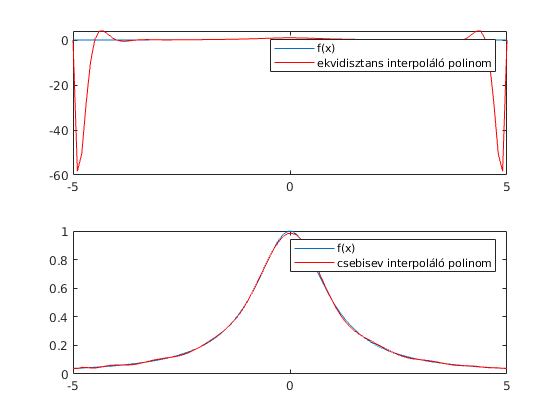
rungellcsebi(21)

Warning: Polynomial is badly conditioned. Add points with distinct X values,
reduce the degree of the polynomial, or try centering and scaling as described
in HELP POLYFIT. 
Warning: Polynomial is badly conditioned. Add points with distinct X values,
reduce the degree of the polynomial, or try centering and scaling as described
in HELP POLYFIT. 

Spline

Szigorúan véve a spline interpoláció annak a feladatnak a megoldása, hogy előírom a függvény értékeit az alappontokban, és ezekre harmadfokú polinomot illesztek szakaszonként úgy, hogy egy polinom két egyás követő pontra illeszkedik, és az alappontokban az így kialakuló interpoláló függvénytől (amely szakaszonként polinom) elvárjuk, hogy legyen érintő és görbület folytonos. Ez még kevés az egyértelműséghez, ezt azzal a két feltétellel egészítjük ki, hogy x_0-ban és x_n -ben előírjuk az első vagy második derivált értékét.

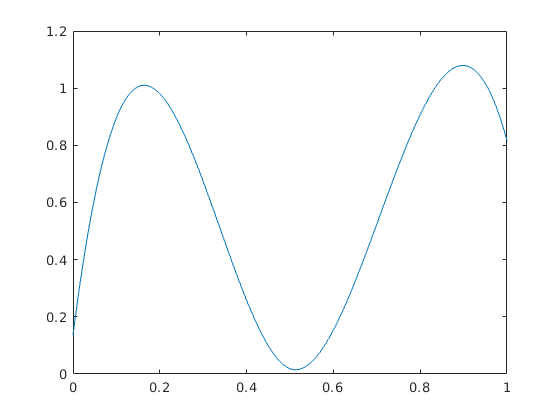
figure(2)
ertekek=spline(0:0.25:1, rand(1,5),t);
plot(t,ertekek)

Published with MATLAB® R2018b