1996/97 tél II. Villamosmérnök 13.-18.tk.
1.
Számítsuk ki az
![]() egyenletu felület felszínét!
egyenletu felület felszínét!
MO.
![]()
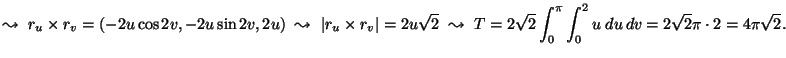
2.
Számítsuk ki
![]() értékét, mint
r függvényét minden
értékét, mint
r függvényét minden
![]() -re ha
-re ha ![]() !
!
MO.
![]()
3.
Legyen N az [xy]-síkbeli a
![]() csúcspontú négyzetvonal és
v(x,y) = (2x + 2y2, 2y + 2x2)
kétdimenziós
vektorfüggvény. Számítsuk ki v felületmenti
integrálját N-en, mint egy kétdimenzióbeli valódi
felületen!
csúcspontú négyzetvonal és
v(x,y) = (2x + 2y2, 2y + 2x2)
kétdimenziós
vektorfüggvény. Számítsuk ki v felületmenti
integrálját N-en, mint egy kétdimenzióbeli valódi
felületen!
MO.
Mivel
![]() , így T-re
alkalmazva a Gauss-Osztrogradszkij tételt (V a T határú
négyzetlap):
, így T-re
alkalmazva a Gauss-Osztrogradszkij tételt (V a T határú
négyzetlap):
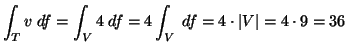 .
.
4. Legyen G az
origóközéppontú
gömbfelület a
háromdimenziós térben.
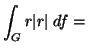 ?
?
MO.
Legyen
![]() ,
n a gömb normálisa, vn pedig
v-nek
n-re eso vetülete. Ekkor
,
n a gömb normálisa, vn pedig
v-nek
n-re eso vetülete. Ekkor
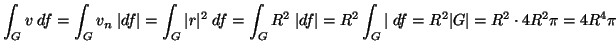 .
.
5.
Hol létezik hatérértéke az
![]() komplex függvénynek?
komplex függvénynek?
MO.
Az y tengely kivételével mindenütt, mert folytonosok
hányadosa. Az
y tengelyen nem, mert
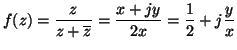 és nyilván
és nyilván
![]() -nek nincs határértéke ha
-nek nincs határértéke ha
![]() még az origóban sem (valóban itt is pl.
az y = x mentén 1-hez, míg y = 2x mentén 2-höz
tart).
még az origóban sem (valóban itt is pl.
az y = x mentén 1-hez, míg y = 2x mentén 2-höz
tart).
6.
Számítsuk ki a
![]() értékét !
értékét !
MO.
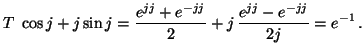
7.
Legyen K(w) az egységnyi sugarú w középpontú
kör a komplex síkon és
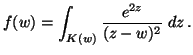 Számítsuk ki az f'(1) értékét (ha létezik) !
Számítsuk ki az f'(1) értékét (ha létezik) !
MO.
A deriváltakra vonatkozó Cauchy-féle
integrálformulával n = 1-re:
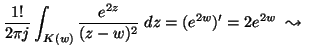
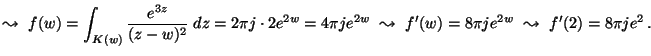
8.
Legyen K az egységnyi sugar, origóközéppontú
kör. Mennyi az
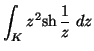 integrál
értéke?
integrál
értéke?
MO.
![]() Taylor-sora:
Taylor-sora:
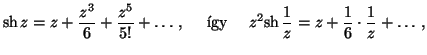 tehát
a függvény residuuma a nullában
tehát
a függvény residuuma a nullában ![]() vagyis az integrál
értéke:
vagyis az integrál
értéke:
![]()