1996/97 tél II. Villamosmérnök 13.-18.tk.
1.
Határozzuk meg az
![]() kétdimenzióbeli
valódi felület P = (2,4) pontbeli érintosíkjának
egyenletét!
kétdimenzióbeli
valódi felület P = (2,4) pontbeli érintosíkjának
egyenletét!
MO.
![]()
(Valóban, az érintosík az
y = x2-nek az x=2-beli érintoje,vagyis (mivel y'(2) = 4)
az
![]() egyenes.)
egyenes.)
2.
Adjunk meg egy olyan u = u(r) skalárfüggvényt a síkban,
hogy
![]() legyen minden síkbeli
legyen minden síkbeli ![]() esetén!
esetén!
MO.
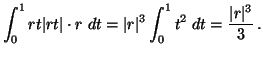
3.
Legyen K a síkbeli kifele irányított
origóközéppontú körvonal.
Számítsuk ki a
![]() síkvektorfüggvény felületmenti
integrálját K-n, mint egy kétdimenzióbeli valódi
felületen!
síkvektorfüggvény felületmenti
integrálját K-n, mint egy kétdimenzióbeli valódi
felületen!
MO.
K normálisa minden pontjában r irányú, így
meroleges
![]() -re, tehát v-nek a normálisra eso
vetülete
-re, tehát v-nek a normálisra eso
vetülete
![]() ezért
ezért
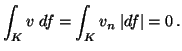
Valóban:
![]() miatt
Gauss-Osztrogradszkij
tétellel (V a körlap):
miatt
Gauss-Osztrogradszkij
tétellel (V a körlap):
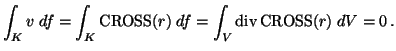 4.
Legyen L az
4.
Legyen L az
![]() egyenletu háromdimenzióbeli görbe.
egyenletu háromdimenzióbeli görbe.
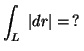
MO.
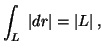 de
L egyenes szakasz, így | L | L két végpontjának távolsága,
tehát
de
L egyenes szakasz, így | L | L két végpontjának távolsága,
tehát
![]()
Valóban
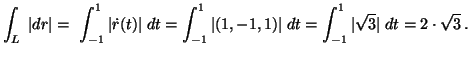
5. Hol deriválható az f(x+jy) = x komplex függvény?
MO.
Sehol, mert az egyik Cauchy-Riemann d.e. nem áll fenn, hiszen
![]() tehát
tehát
![]()
6.
Határozzuk meg azt a tartományt, melybe a
![]() körlapot az
körlapot az
![]() komplex függvény
képezi!
komplex függvény
képezi!
MO.
![]()
![]()
7.
Legyen K egységnyi sugarú, origóközéppontú
kör. Mennyi az
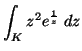 integrál értéke?
integrál értéke?
MO.
ez Taylor-sora:
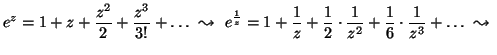
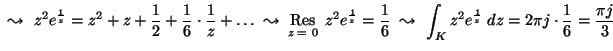
8.
Adjunk meg egy olyan z = 0 körüli Laurent-sort, mely
eloállítja az
az
![]() függvényt a z = 2-ben!
függvényt a z = 2-ben!
MO.
z-vel végigosztva:
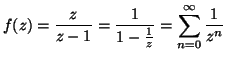 és ez konvergens
ha
és ez konvergens
ha
![]()