1. Vizsgazárthelyi megoldásokkal
1998/99 tél II. évf. 13.-18.tk.
1. Legyen v(r) = (x,y2) egy kétdimenziós vektortér és F az a háromszögvonal, melynek csúcsai az origó, a (0,1) és az (1,0) pontok. Számítsuk ki v fluxusát F-en mint egy kifelé irányított kétdimenzióbeli valódi felületen, kétféleleképpen:
a) a fluxus definíciója alapján közvetklenül v-nek F-en való felületmenti integrálásával
b) a Gauss-Osztrogradszkij tétel alapján.
MO. a) A tengelyek mentén a fluxus nulla, mert a
vízszintes
tengely pontjaiban csak vízszintes, a függoleges tengely
pontjaiban pedig csak függoleges komponense van a
függvénynek, így itt a felületi normális és a
függvény egymásra merolegesek. Ami az F átfogót
illeti, egy egyenlete (melynek esetén a térrészbol
kifele van irányítva:
![]() .
Így
.
Így
tehát a) a fluxus
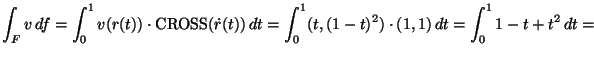
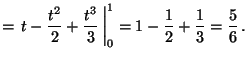 b)
b)
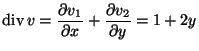 ,
így Gauss-Osztogradszkij tétellel a fluxus
(a háromszöglapot V-vel jelölve):
,
így Gauss-Osztogradszkij tétellel a fluxus
(a háromszöglapot V-vel jelölve):
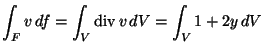
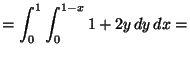
![${\displaystyle
=\int_0^1 y + y^2\,{\,\rule[-2mm]{0.12mm}{5mm}\,}_0^{1-x}\,dx = }$](img8.gif)
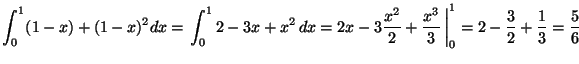 .
.
2. Számítsuk ki a
CROSS
![]() értékét a P = (3,4) pontban!
értékét a P = (3,4) pontban!
MO.
![]() (VAGY koordinátánként:
(VAGY koordinátánként:
![]()
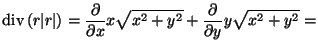
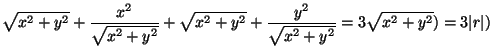 ,
,
így
![]() ,
tehát
CROSS
,
tehát
CROSS
![]() ,
vagyis
,
vagyis
![]()
![]()
3. Határozzuk meg a
v(x,y) = (x2+y2, 2xy)
vektorfüggvény
potenciáját, ahol az létezik!
MO.
tehát mindenütt van potenciál.
![]() tehát
tehát
![]() azaz
azaz
![]() ,
vagyis
,
vagyis
![]() ,
így
,
így
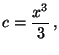 amibol
amibol
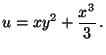
4. Legyen
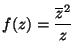 ha
ha ![]() és
és
![]() Hol folytonos az
f függvény?
Hol folytonos az
f függvény?
MO. Mindenütt, mert ![]() esetén folytonos
függvényekbol
származik folytonosságot megorzo módon és
esetén folytonos
függvényekbol
származik folytonosságot megorzo módon és
5. K egységnyi sugarú, origó középpontú
kör. Mekkora az
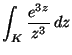 integrál ?
integrál ?
MO. Cauchy integrálformulával
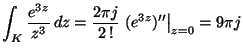 .
.
6. Határozza meg a
![]() függvény azon z
= -1
pont körüli Laurent sorát, mely a z = 1 pontban
eloállítja a függvényt!
függvény azon z
= -1
pont körüli Laurent sorát, mely a z = 1 pontban
eloállítja a függvényt!
MO.