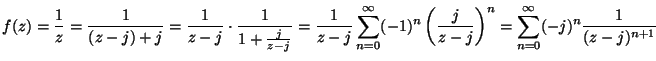1. Legyen
![]() egy kétdimenziós
vektortér és
egy kétdimenziós
vektortér és
![]() az a háromszögvonal, melynek csúcsai az origó, a
(0,1)
és az (1,0) pontok. Számítsuk ki
az a háromszögvonal, melynek csúcsai az origó, a
(0,1)
és az (1,0) pontok. Számítsuk ki ![]() fluxusát
fluxusát ![]() -en
mint egy kifelé irányított kétdimenzióbeli
valódi felületen és
-en
mint egy kifelé irányított kétdimenzióbeli
valódi felületen és ![]() cirkulációját
cirkulációját ![]() -en mint
egy pozitívan irányított kétdimenzióbeli
görbén!
-en mint
egy pozitívan irányított kétdimenzióbeli
görbén!
MO.
a)
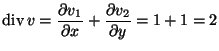 ,
így Gauss-Osztogradszkij tétellel a fluxus
(a háromszöglapot
,
így Gauss-Osztogradszkij tétellel a fluxus
(a háromszöglapot ![]() -vel jelölve):
-vel jelölve):
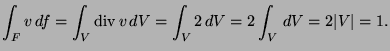 b)
b)
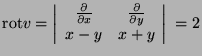 ,
így Stokes tétellel a cirkuláció (a
háromszöglapot
,
így Stokes tétellel a cirkuláció (a
háromszöglapot ![]() -vel jelölve):
-vel jelölve):
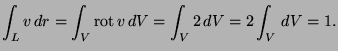
2. Számítsuk ki a
rot
![]() div
div ![]() értékét a
értékét a
![]() pontban!
pontban!
MO.
div ![]() div
div ![]() grad
grad ![]() és
rot
és
rot ![]() rot
rot ![]() CROSS
CROSS ![]() grad
grad ![]()
![]() CROSS
CROSS ![]() (VAGY koordinátánként:
(VAGY koordinátánként:
![]()
![]()
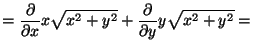
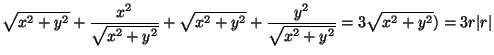 és
és
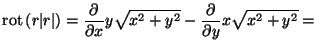
![]() .
.
Végülis tehát
rot ![]() div
div ![]() rot
rot ![]() rot
rot ![]() .
.
3. Adjunk meg egy olyan
![]() skalár-függvényt, melyre fennáll, hogy grad
skalár-függvényt, melyre fennáll, hogy grad
![]() minden
minden
![]() esetén!
esetén!
MO.
![]()
![]() (VAGY:
(VAGY:
![]()
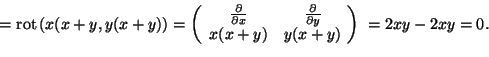 )
Tehát mindenütt
)
Tehát mindenütt
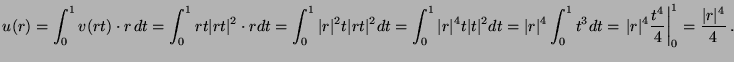
(VAGY:
![]() , így
, így
![]() tehát
tehát
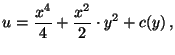 azaz
azaz
![]() , vagyis
, vagyis
![]() , így
, így
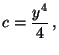 amibol
amibol
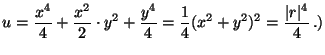
4. Legyen
![]() ha
ha ![]() és
és
![]() Hol folytonos az
Hol folytonos az
![]() függvény?
függvény?
MO. Az origó kivételével mindenütt, mert
![]() esetén
folytonos függvényekbol származik folytonosságot
megorzo módon és
esetén
folytonos függvényekbol származik folytonosságot
megorzo módon és
![]() ,
,
![]() -
nek pedig nincs határértéke az origóban, hiszen az
-
nek pedig nincs határértéke az origóban, hiszen az ![]() tengely
mentén:
tengely
mentén:
![]() , míg az y tengely
mentén
, míg az y tengely
mentén
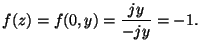
5. ![]() egységnyi sugarú, origó középpontú
kör és
egységnyi sugarú, origó középpontú
kör és ![]() tetszoleges egész szám.
tetszoleges egész szám.
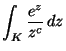 = ?
= ?
MO. Ha ![]() nem pozitív, akkor, mivel az integrandus
reguláris,
az integrál 0. Egyebként Cauchy
integrál-formulával, vagy
residuum-tétellel:
nem pozitív, akkor, mivel az integrandus
reguláris,
az integrál 0. Egyebként Cauchy
integrál-formulával, vagy
residuum-tétellel:
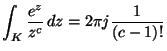
6. Határozza meg a
![]() függvény azon
függvény azon
![]() pont körüli Laurent sorát mely a
pont körüli Laurent sorát mely a ![]() pontban
eloállítja a függvényt!
pontban
eloállítja a függvényt!
MO.