2. Vizsgazárthelyi megoldásokkal
1999/2000 tél II. évf. 13.-18.tk.
1. Legyen F az [xy] síkban fekvo
R sugarú origóközéppontú
felfelé irányított
körlap és k a z tengely irányú egységvektor.
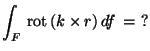
MO. F normálisa n=k, legyen
![]() erre eso
vetülete vn.
erre eso
vetülete vn.
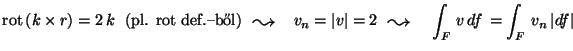
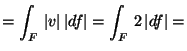
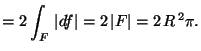 VAGY
VAGY
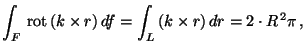 ahol
ahol
L a körvonal (lásd Jegyzet 1.23(1) ).
2.
Számítsuk ki a div
![]() értékét
minden
értékét
minden
![]() esetén!
esetén!
MO.
![]() .
.
3.
Legyen H az a háromszögvonal (mint kétdimenzióbeli
felület), melynek csúcsai a
![]() pontok. Legyen
v(x,y)=(2x+y2,x2+2y) minden
pontok. Legyen
v(x,y)=(2x+y2,x2+2y) minden
![]() -re.
-re.
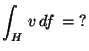
MO.
div
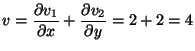 ,
így Gauss-Osztrogradszkij
tétellel (F a H által bezárt
háromszöglap):
,
így Gauss-Osztrogradszkij
tétellel (F a H által bezárt
háromszöglap):
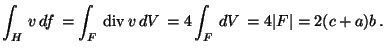
4. Legyen
![]() .
.
![]()
MO.
![]()
5. Adja meg az
![]() függvény
z = 1 és z = 0 körüli összes
Laurent sorát!
MO.
függvény
z = 1 és z = 0 körüli összes
Laurent sorát!
MO.
a) z = 0:
![]() |z|>0
|z|>0
b) z = 1:
1)
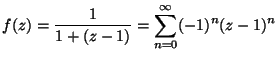 (|z-1|<1)
(|z-1|<1)
2)
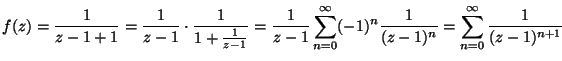 (|z-1|>1)
(|z-1|>1)
6.
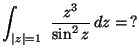
MO.
![]() iff
iff
![]() iff
iff
![]() iff
ejz=e-jz iff
iff
ejz=e-jz iff
![]() iff
iff
iff
![]() iff
iff
![]() így
így
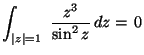 ,
,
mert
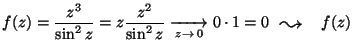 -nek az egyetlen a
körlapon levo
szingularitásában, az origóban megszüntetheto
szakadása van.
-nek az egyetlen a
körlapon levo
szingularitásában, az origóban megszüntetheto
szakadása van.