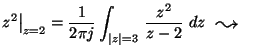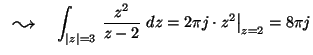
3. Vizsgazárthelyi megoldásokkal
1999/2000 tél II. évf. 13.-18.tk.
1. Legyen F az
R sugarú origóközéppontú
kifelé irányított gömb és
![]()
MO. F normálisa
![]() ,
így v(r)-nek a normálisra való vetülete:
vn(r)=|v(r)|=|r|3. Másrészt a gömbön |r|=R, így
a gömbön
vn(r)=|v(r)|=R3. Mindezekkel
,
így v(r)-nek a normálisra való vetülete:
vn(r)=|v(r)|=|r|3. Másrészt a gömbön |r|=R, így
a gömbön
vn(r)=|v(r)|=R3. Mindezekkel
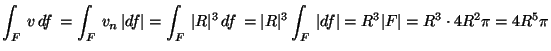
2.
Számítsuk ki a grad
![]() értékét
minden
értékét
minden
![]() esetén!
esetén!
MO.
![]()
![]()
3.
Legyen K az [xy] síkbeli origóközéppontú
pozitívan irányított R sugarú
körvonal és
![]() minden
minden
![]() -re.
-re.
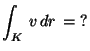
MO. rot
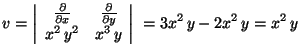 így
Stokes tétellel (F a K által bezárt
körlap):
így
Stokes tétellel (F a K által bezárt
körlap):
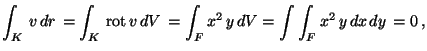 mert F az x tengelyre szimmetrikus és az integrandus
y-ban páratlan.
mert F az x tengelyre szimmetrikus és az integrandus
y-ban páratlan.
4. Határozza meg azt a tartományt, melybe az
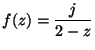 függvény
a
függvény
a
![]() tartományt képezi!
tartományt képezi!
MO.
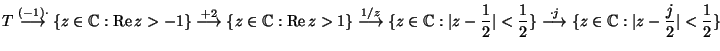 .
.
5. Számítsa ki az
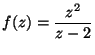 függvény
100. deriváltját az origóban!
MO. Az
függvény
100. deriváltját az origóban!
MO. Az
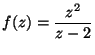 függvény origó körüli Taylor-sora:
függvény origó körüli Taylor-sora:
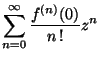
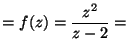
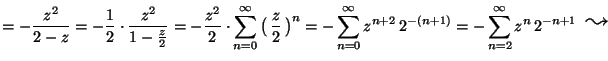
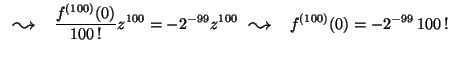
6.
a)
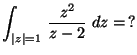 b)
b)
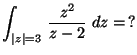
MO. a) Az integrandus a körön belül reguláris, tehát Cauchy integráltétellel az integrál 0.
b) z2 mindenütt reguláris, tehát
Cauchy integrálformulával: