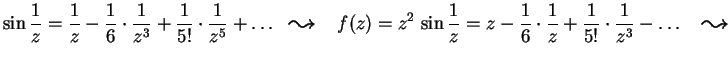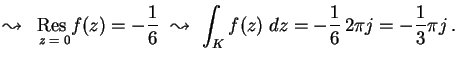1. Vizsgazárthelyi megoldásokkal

2000/01 tél II. Villamosmérnök 13.-18.tk.

1. Legyen H az a háromszögvonal, melynek csúcsai a (-2,0), (0,2) , (2,0) pontok a síkban. Legyen $v(x,y) = (2\,y - x^2, y^2 -2\,x)$ egy kétdimenziós vektorfüggvény. Számítsuk ki v vonalmenti integrálját H-n!

MO. ${\rm rot} \, v = \frac{\partial v_2}{\partial x}- \frac{\partial v_1}{\partial y} = -2 -2 = - 4 \,$ , így Stokes tétellel (F a H által bezárt háromszöglap):

${\displaystyle \int_H v \; dr = \int_F {\rm rot} \,v \; dV = - 4 \int_F \; df = - 4 \, \vert F \vert = - 16 \, }$.

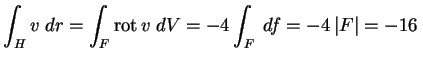2. Legyen G az origóközéppontú R sugarú gömbfelület a háromdimenziós térben. ${\displaystyle \int_G \frac{r}{\vert r \vert} \; df =\,? }$

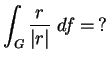
MO. Legyen $v(r) = \frac{r}{\vert r\vert} \,$, n a gömb normálisa, v_n pedig v-nek n-re eso vetülete. Ekkor $v \,\vert\vert\, n \mbox{\,\,\,\,\raisebox{-0.5mm}{\Large$\leadsto$ }\,\,\,\,}v_n = \vert v\vert$, így ${\displaystyle \int_G v \; df = \int_G v_n \; \vert df \vert = \int_G \left\ve... ...G \frac{R}{R}\;\vert df\vert = \int_G \;\vert df\vert =\vert G\vert=4R^2 \pi\,}$.

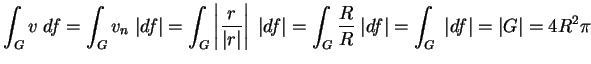3. Számítsuk ki ${\rm div \, grad} \vert r \vert^2$ értékét, mint r függvényét minden $r \in {\bf R}^4$-re ha $r \neq 0$! MO. ${\displaystyle {\rm grad} \vert r \vert^2 = 2 \vert r \vert \cdot {\rm grad} \... ... \vert r \vert^2 = {\rm div} \, 2 r = 2 \,{\rm div} \, r = 2 \cdot 4 = 8 \,. }$

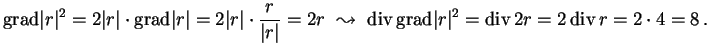
4. Számítsuk ki a $\sin j + j \cos j$ értékét !

MO. ${\displaystyle \,\, \sin j + j \cos j = \frac{e^{jj} - e^{-jj}}{2\,j} + j \,\... ...-jj}}{2} = \frac{j}{2}\,\left(-e^{jj} + e^{-jj}+e^{jj} + e^{-jj}\right)= j\,e}$

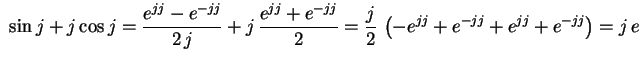
5. ${\displaystyle \lim_{z \longrightarrow 0} \frac{\frac{e^z - 1}{z} - 1}{z} = }$ ?

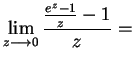MO. e^z Taylor-sora:

${\displaystyle e^z = 1 + z + \frac{z^2}{2} + \frac{z^3}{6} + \ldots \, \mbox{\... ...s \, \longrightarrow \frac{1}{2} \mbox{ \ \ \ ha \ \ \ } z \longrightarrow 0 }$

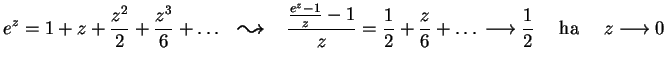
6. Legyen K egységnyi sugarú, origóközéppontú kör. Mennyi az 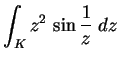${\displaystyle \int_K z^2\,\sin \frac{1}{z} \; dz }$ integrál értéke?

MO. ${\displaystyle \sin \frac{1}{z} = \frac{1}{z}- \frac{1}{6} \cdot \frac{1}{z^3}... ... \ldots \,\, \mbox{\,\,\,\,\raisebox{-0.5mm}{\Large$\leadsto$ }\,\,\,\,}\,\,}$

${\displaystyle \leadsto \,\ {\rm Res}\, \hspace{-6.8mm} \raisebox{-1.6ex}{{\sc... ...dsto \,\, \int_K f(z) \; dz = - \frac{1}{6}\, 2\pi j = - \frac{1}{3}\pi j \,.}$