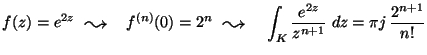2000/01 tél II. Villamosmérnök 13.-18.tk.
1.
Legyen H az a háromszögvonal, melynek csúcsai
a (0,0), (0,2) , (2,0) pontok a síkban.
Legyen
![]() egy
kétdimenziós
vektorfüggvény.
Számítsuk ki v
felületmenti integrálját a kifelé irányított H-n!
egy
kétdimenziós
vektorfüggvény.
Számítsuk ki v
felületmenti integrálját a kifelé irányított H-n!
MO.
![]() , így Gauss-Osztrogradszkij
tétellel:
(F a H által bezárt háromszöglap):
, így Gauss-Osztrogradszkij
tétellel:
(F a H által bezárt háromszöglap):
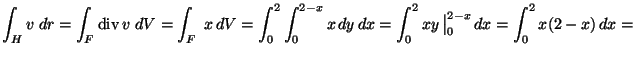
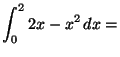
![${\displaystyle=\rule[-6mm]{0.0mm}{15mm}
(\left.x^2-\frac{x^3}{3})\,\right\vert _0^2=
4-\frac{8}{3}= \frac{4}{3}}$](img6.gif)
VAGY: a tengelyek mentén a felületi integrál 0, mert az x tengely mentén: v(x,0)=(x2,0), melynek csak x irányú, tehát a normálisra meroleges komponense van és u.így a másik tengely esetén. Tehát csak az átfogóra kell kiszámítani a felületi integrált. Ennek egyenlete:
![]()
![]()
![]()
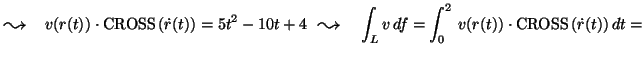
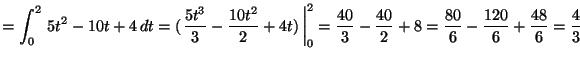
2. Legyen H az a z tengelyu R
sugarú h magasságú (háromdimenzióbeli)
egyenes körhengerpalást, melynek
alapköre az [x,y] síkban van.
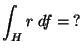
MO.
Legyen
![]() , n a hengerpalást normálisa,
vn pedig v-nek n-re eso vetülete.
Ekkor a hengerpaláston mindenütt vn=R
így
, n a hengerpalást normálisa,
vn pedig v-nek n-re eso vetülete.
Ekkor a hengerpaláston mindenütt vn=R
így
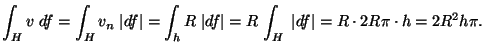
VAGY: a hengerpalást egyenlete:
![]()
![]()
![]()
3.
Számítsuk ki
![]() értékét, mint
r függvényét minden
értékét, mint
r függvényét minden
![]() -re ha
-re ha ![]() !
MO.
!
MO.
![]()
![]() (
(![]() ).
).
4.
Számítsuk ki a
![]() értékét !
értékét !
MO.
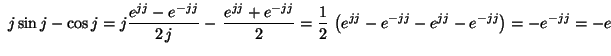 .
.
5.
![]()
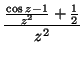 = ?
= ?
MO. Legyen f(z) a fenti függvény.
![]() Taylor-sora:
Taylor-sora:
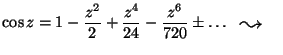
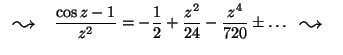
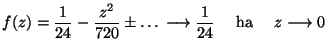
VAGY: L'Hospitallal:
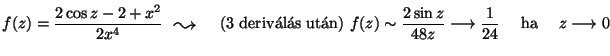
6. Legyen K egységnyi sugarú, origóközéppontú kör és n >0 tetszoleges természetes szám.
Mennyi az
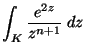 integrál értéke?
integrál értéke?
MO.
A Cauchy integrálformula szerint:
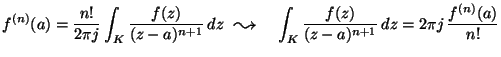
Itt most ![]() és
és