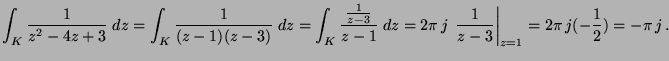1.
Legyen ![]() az a háromszögvonal, melynek csúcsai
a (0,0), (0,2) , (2,0) pontok a síkban.
Legyen
az a háromszögvonal, melynek csúcsai
a (0,0), (0,2) , (2,0) pontok a síkban.
Legyen
![]() egy
kétdimenziós
vektorfüggvény.
Számítsuk ki
egy
kétdimenziós
vektorfüggvény.
Számítsuk ki ![]() vonalmenti integrálját a pozitívan
irányított
vonalmenti integrálját a pozitívan
irányított ![]() -n!
-n!
MO.
![]() , így Stokes
tétellel:
(
, így Stokes
tétellel:
(![]() a
a ![]() által bezárt háromszöglap):
által bezárt háromszöglap):
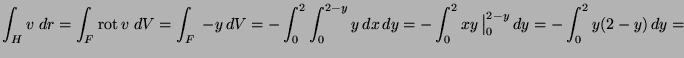
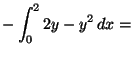
![$ {\displaystyle=\rule[-6mm]{0.0mm}{15mm}
\left.\frac{y^3}{3}-x^2\,\right\vert _0^2=
\frac{8}{3}-4= -\frac{4}{3}}$](img8.png)
VAGY: a tengelyek mentén a vonalintegrál 0, mert
az ![]() tengely mentén:
tengely mentén:
![]() , melynek csak
, melynek csak
![]() irányú, tehát az érintore meroleges komponense
van és u.így a másik tengely esetén. Tehát csak az
átfogóra kell kiszámítani a felületi integrált.
Ennek egyenlete ha
irányú, tehát az érintore meroleges komponense
van és u.így a másik tengely esetén. Tehát csak az
átfogóra kell kiszámítani a felületi integrált.
Ennek egyenlete ha ![]() -et negatívan irányítjuk:
-et negatívan irányítjuk:
![]()
![]()
![]()
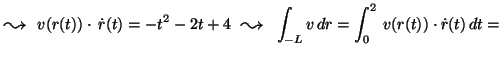
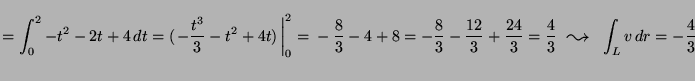
2. Legyen ![]() és
és ![]() a
háromdimenziós térben
az a
a
háromdimenziós térben
az a ![]() síkban
elhelyezkedo
síkban
elhelyezkedo ![]() sugarú felfelé irányított
körlap, melynek
középpontja a
sugarú felfelé irányított
körlap, melynek
középpontja a ![]() tengelyen van.
tengelyen van.
MO.
Legyen
![]() ,
, ![]() a körlap normálisa,
a körlap normálisa,
![]() pedig
pedig ![]() -nek
-nek ![]() -re eso vetülete.
Ekkor a körlapon mindenütt
-re eso vetülete.
Ekkor a körlapon mindenütt ![]() így
így
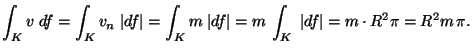
VAGY: a körlap egyenlete:
![]()
![]()
![]()
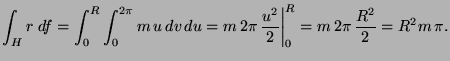
3. Adjunk meg egy olyan
![]() -en értelmezett
-en értelmezett
![]() skalárfüggvényt, hogy
skalárfüggvényt, hogy
![]() legyen minden
legyen minden
![]() esetén!
esetén!
MO.
![]() potenciálja:
potenciálja:
 Valóban:
Valóban:
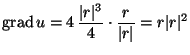 .
.
4.
Számítsuk ki a
![]() értékét !
értékét !
MO.
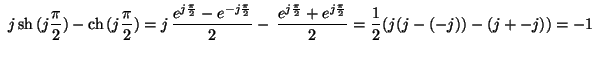 .
.
5.
Legyen minden ![]() esetén
esetén
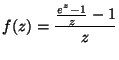 .
Folytonossá teheto-e az
.
Folytonossá teheto-e az ![]() függvény
az origóban? Ha igen, a folytonosított változat
deriválható-e az origóban? Ha igen, mennyi a derivált
értéke?
függvény
az origóban? Ha igen, a folytonosított változat
deriválható-e az origóban? Ha igen, mennyi a derivált
értéke?
MO. ![]() Taylor-sora:
Taylor-sora:
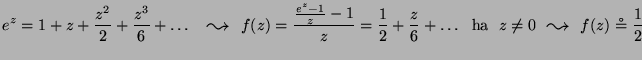 esetén
esetén ![]() egy mindenütt konvergens
hatványsor határfüggvénye, így mindenütt
akárhányszor deriválható, Taylor-sora az ot
eloállító hatványsor
egy mindenütt konvergens
hatványsor határfüggvénye, így mindenütt
akárhányszor deriválható, Taylor-sora az ot
eloállító hatványsor
![]() .
.
6.
Legyen ![]() az origóközéppontú
az origóközéppontú ![]() sugarú kör. Mennyi az
sugarú kör. Mennyi az
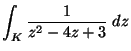 integrál
értéke?
integrál
értéke?
MO. Cauchy integrálformulával: