Tail asymptotics of free path lengths for the periodic Lorentz process. On Dettmann's "Horizon" Conjectures. (submitted, with P. N\'andori and T. Varj\'u) arXiv:1210.2231

Some challenges in the theory of (semi)-dispersing billiards. Nonlinearity, invited paper, 21:187-193 2008.

Limit Theorems for Perturbed Lorentz Processes, Duke Math. Journal, 148: 459-499, 2009 (with D. Dolgopyat and T. Varjú)

Recurrence Properties of Planar Lorentz Process, Duke Math. Journal, 142: 241-281, 2008 (with D. Dolgopyat and T. Varjú).

Limit Laws and Recurrence for the Planar Lorentz Process with Infinite Horizon, J. Statist. Phys. 129:59-80, 2007. (with T. Varjú)

Local Limit Theorem and Recurrence for the Planar Lorentz Process, Ergodic Theory and Dynamical Systems, 24 (2004), 257-278 (with T. Varjú)

Multi-dimensional Semi-Dispersing Billiards: Singularities and the Fundamental Theorem, Annales Henri Poincaré, 3 (2002), 451-482 (with P. Bálint, N. Chernov, I. P. Tóth)

Hard Ball Systems are Completely Hyperbolic, Annals of Mathematics, 149 (1999), 35-96 (with N. Simányi)

The K-Property of `Orthogonal' Cylindric Billiards. Commun. Math. Phys. 160 (1994), 581-597

A ,Transversal' Fundamental Theorem for Semi-Dispersing Billiards. Commun. Math. Phys.. 129 (1990) 535-560 (with A. Krámli and N. Simányi) Erratum: ibidem 129 (1991) 207-208

The K-Property of Three Billiard Balls. Annals of Mathematics. 133 (1991), 37-72 (with A. Krámli and N. Simányi)

Towards a unified dynamical theory of the Brownian particle in an ideal gas. Commun. Math. Phys.. 111(1987), 41- 62. (with B. Tóth)

On the effect of collisions on the motion of an atom in 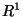Ann. of Probability. 8(1980), 1968-1078. (with P. Major)

A problem of two lifts. Ann. of Probability. 5(1977), 550-559.

On a problem of Cox concerning controlled variability processes in 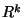Ann. of Probability. 3(1975), 597-607. (with P. Gács)

Limit theorems for the distribution of the sums of a random number of random variables. Ann. of Math. Statistics, 43(1972), 1902-1913.