Sample Final Exam
Mathematics A2
May, 2009
1. a.) ( 3 points) Put down Leibniz criteria for the convergence of alternating numerical series.
b.) (4 points) Can
we select the coefficients 
of
the power series 
such that
the series
(1) converges for every 
,
(2) converges absolutely for every ,
(3) converges conditionally for every ,
(4) has no point of convergence.
If your answer YES, show an example, if your answer is NO, give reason in each case.
2. (8 points) Answer if the following statement is true or false. If you say TRUE, give a proof, if you say NO, give a counterexample.
(1) A set of
two vectors in 
can
be a linearly independent system.
(2) A set of
two vectors in can be a basis
for .
(3) A set of
four vectors in can
be a linearly independent system.
(4) A set of
four vectors in can be a basis
for .
3. a.) (3 points) Give the definition
of the double
integral of the function 
over
the region R.
b.) (3 points) Is it possible that
the value for the integral 
is 
over
the region 
? Give reason
for your answer. (You are
not required to evaluate the
integral.)
4. ( 7 points) Find the first 4 nonzero terms of the Fourier-series of the the periodic function:
, if 
, otherwise
.
5. ( 6 points) Find the values of the parameter a (if possible) such that the following system have infinitely many solutions. Solve the system for these a values:
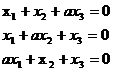
6. (7 points) Give the maximum value of the function
subjected
to the constrain 
.
7. (6 points) Find
the value of the double
integral 
over
the triangular region with vertices
A(0;0), B(1;1) and C(2;0).
8. (7 points) Find
the value of the double
integral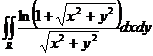 
over
the region 
.
9. (6 points) Find
all points for the curve 
at
which the tangent line is parellel to the
xz plane. Give the
equation of the tangent line
at these points.
Total score: 60 points
Passing limit: 24 points