Department of Stochastics

BME Institute of Mathematics, Department of Stochastics

Contents

Stochastics Research Group

Actualities

English language MSc


	Selected publications and mathematical gallery

Mathematical aspects of classical and quantum statistical physics. Percolation models with short or long range correlations, Ising and Heisenberg models, conformally invariant processes in the plane, noise sensitivity.

Gábor Pete, Balázs Ráth, Bálint Tóth.

A. Hammond, G. Pete, O. Schramm: Local time on the exceptional set of dynamical percolation, and the Incipient Infinite Cluster. Annals of Probability, to appear.
H. Duminil-Copin, C. Garban, G. Pete: The near-critical planar FK-Ising model. Comm. Math. Phys. 326 (2014), 1-35.
C. Garban, G. Pete, O. Schramm: Pivotal, cluster and interface measures for critical planar percolation. Journ. Amer. Math. Soc. 26 (2013), 939-1024.
C. Garban, G. Pete, O. Schramm: The Fourier spectrum of critical percolation. Acta Mathematica 205 (2010), 19-104.
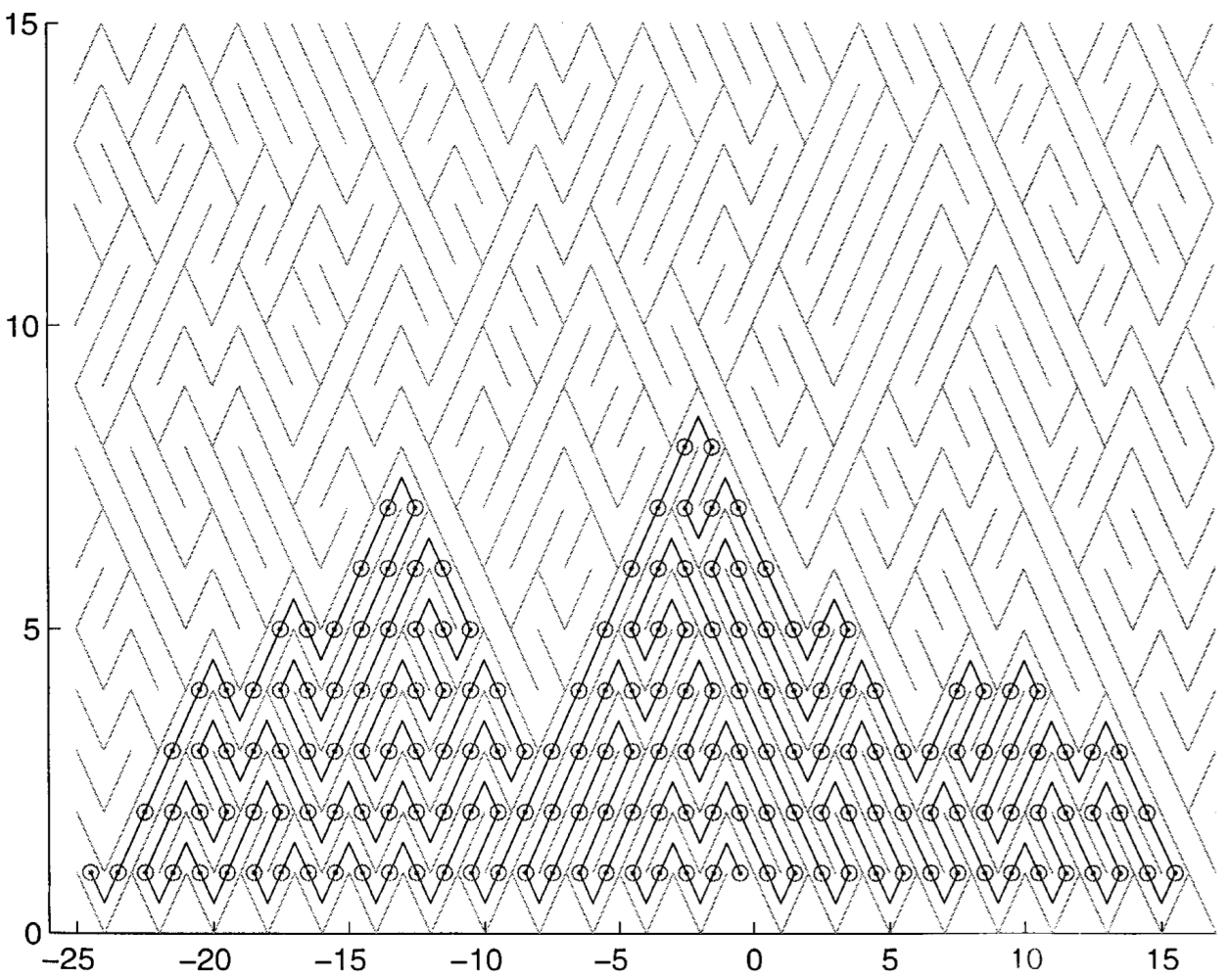
G. Pete: Corner percolation on Z^2 and the square root of 17. Annals of Probability 36 (2008), No. 5, 1711-1747.
G. Pete: A note on percolation on Z^d: isoperimetric profile via exponential cluster repulsion. Electron. Comm. Probab. 13 (2008), 377-392.
B. Ráth, D. Valesin: Percolation on the stationary distributions of the voter model, preprint, 2015.
B. Ráth: A short proof of the phase transition for the vacant set of random interlacements. Electron. Comm. Probab. 20 (2015), paper no. 3, 1-11.
A. Drewitz, B. Ráth, A. Sapozhnikov: An Introduction to Random Interlacements. SpringerBriefs in Mathematics, 2014.
A. Drewitz, B. Ráth, A. Sapozhnikov: On chemical distances and shape theorems in percolation models with long-range correlations. Journal of Mathematical Physics 55 (2014), 083307.
A. Drewitz, B. Ráth, A. Sapozhnikov: Local percolative properties of the vacant set of random interlacements with small intensity. Annales de l'Institut Henri Poincaré 50 (2014), 1165-1197.
T. M. Liggett, J. E. Steif, B. Tóth: Statistical mechanical systems on complete graphs, infinite exchangeability, finite extensions and a discrete moment problem . The Annals of Probability, 35 (2007), 867-914.
B. Tóth. Improved lower bound on the thermodynamical pressure of the S=1/2 quantum Heisenberg ferromagnet. Letters in Mathematical Physics, 28 (1993), 75-84.
B. Tóth. Upper bound on the condensate in hard core Bose lattice gas. Journal of Statistical Physics, 65 (1991), 373-378.

Return times in the system of two falling balls

Singularities in the system of two falling balls

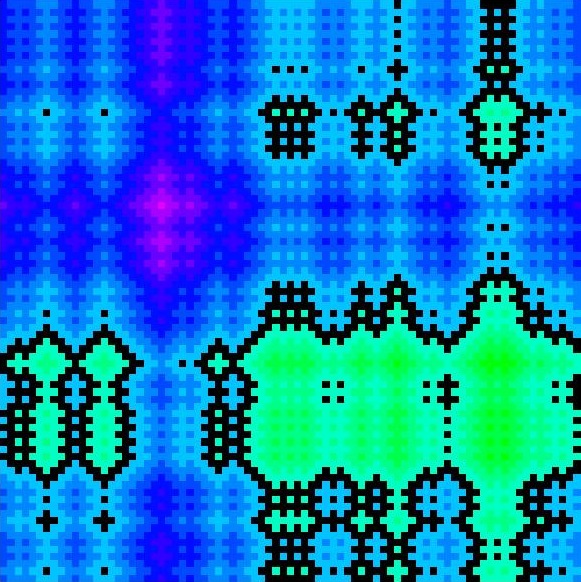
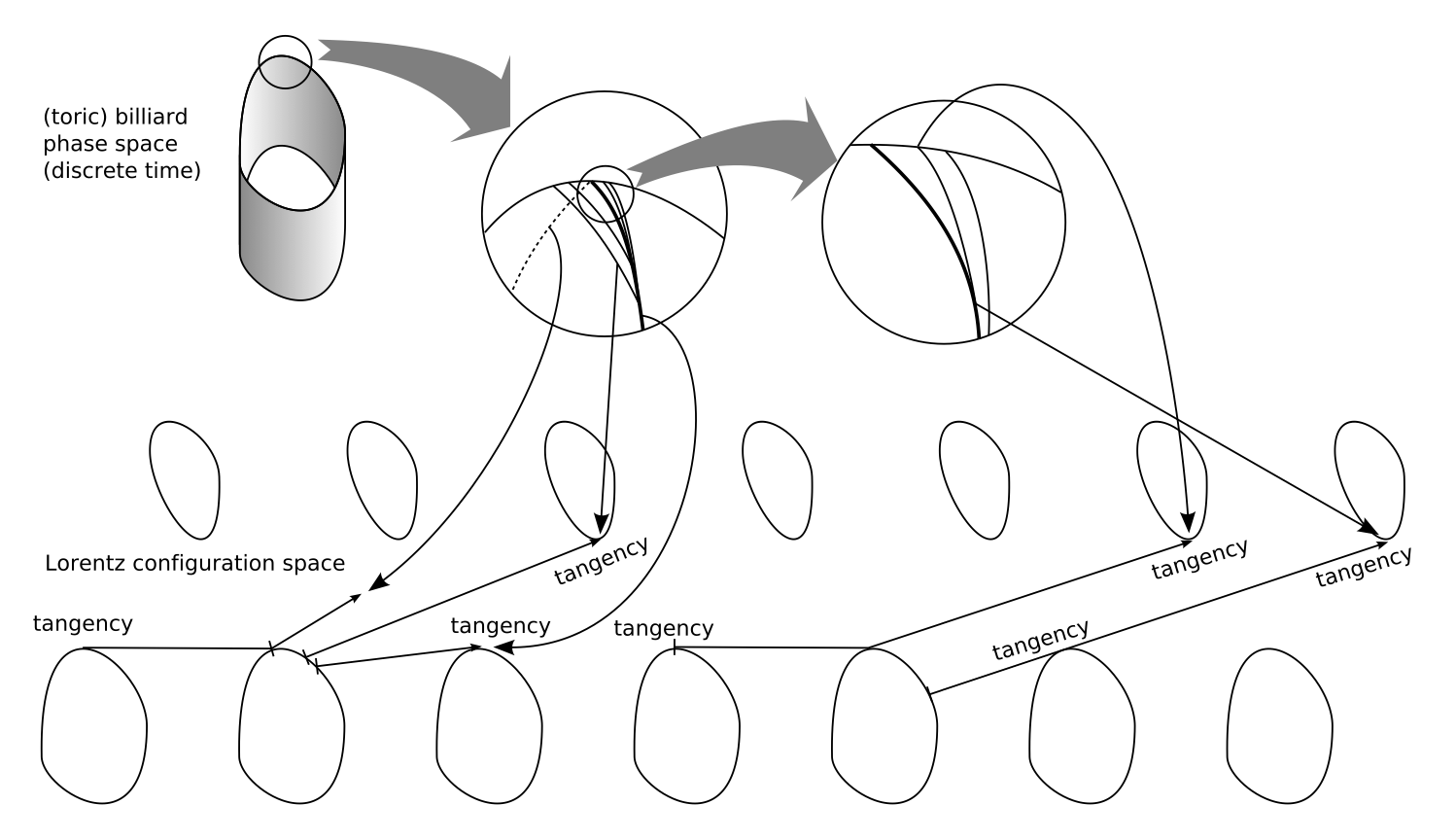
The singularity structure of a billiard system

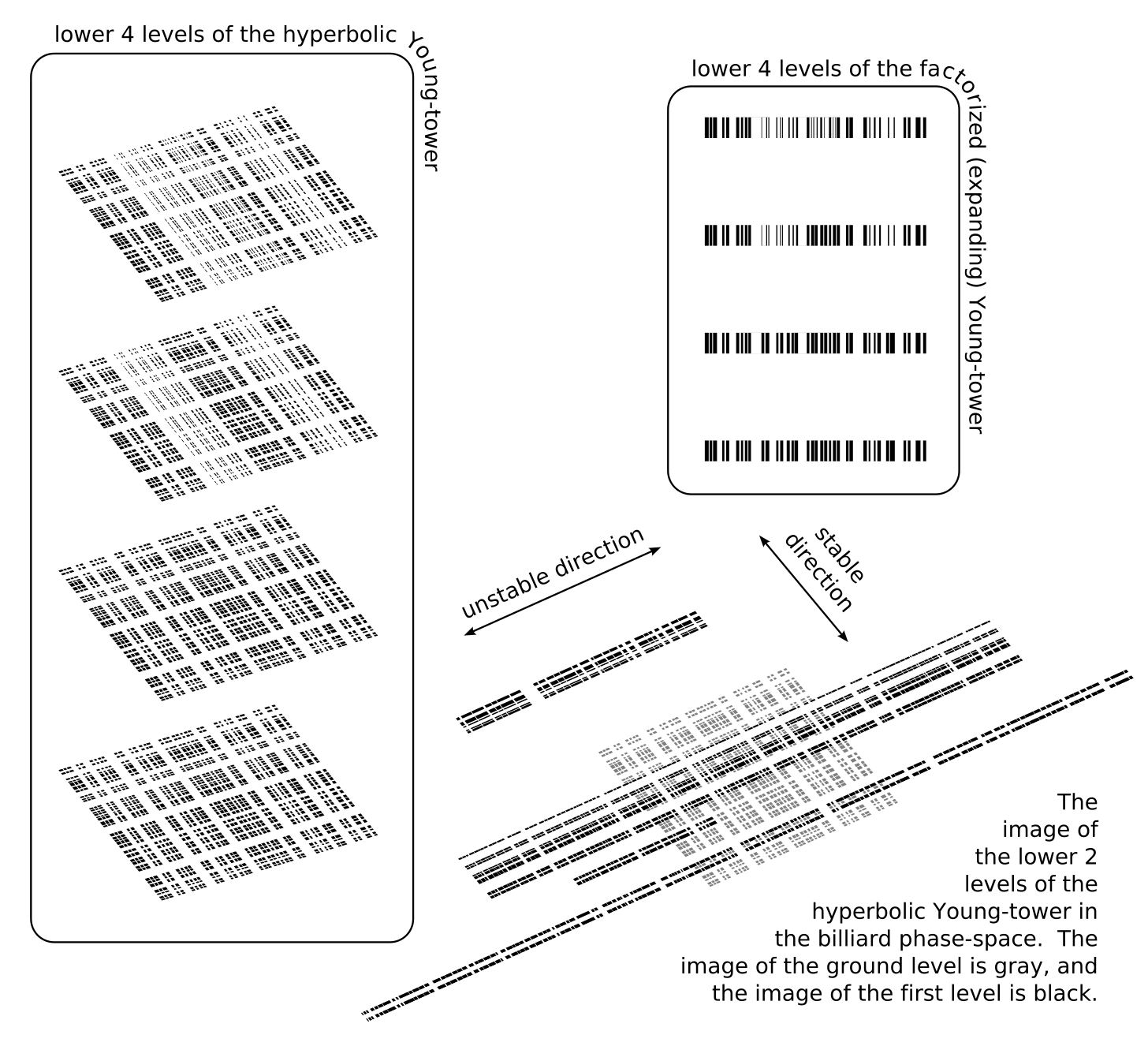
Probabilistic aspects of deterministic dynamical systems. Chaotic behaviour in billiards. Hyperbolicity, ergodicity, correlation decay, limit theorems.

Péter Bálint, Fanni Sélley, Domokos Szász, Imre Péter Tóth

P. Bálint, G. Borbély, A. Némedy Varga: Statistical properties of the system of two falling balls. Chaos 22 (2012), paper 026104.
P. Bálint, N. Chernov, D. Dolgopyat: Limit theorems for dispersing billiards with cusps. Communications in Mathematical Physics 308 (2011)
P. Bálint, K. K. Lin, L-S. Young: Ergodicity and energy distributions for some boundary driven integrable Hamiltonian chains. Communications in Mathematical Physics 294 (2010), 199-228.
P. Nándori, D. Szász, T. Varjú: Tail asymptotics of free path lengths for the periodic Lorentz process: on Dettmann's geometric conjectures. Communications in Mathematical Physics 331 (2014), 111-137.
D. Dolgopyat, D. Szász, T. Varjú: Limit theorems for perturbed Lorentz processes. Duke Math. Journal 148 (2009), 459-499.
D. Szász: Some challenges in the theory of (semi)-dispersing billiards. Nonlinearity, invited paper. 21 (2008), 187-193.
N. Simányi, D. Szász: Hard ball systems are completely hyperbolic. Annals of Mathematics 149 (1999), 35-96.
A. Krámli, N. Simányi, D. Szász: The K-Property of three billiard balls. Annals of Mathematics 133 (1991), 37-72.
P. Bálint, I. P. Tóth: Example for exponential growth of complexity in a finite horizon multi-dimensional dispersing billiard. Nonlinearity 25 (2012), 1275-1297.
P. Bálint, I. P. Tóth: Exponential decay of correlations in multi-dimensional dispersing billiards. Annales Henri Poincaré 9 (2008), 1309-1369. (Prized paper.)
P. Bálint, N. Chernov, D. Szász, I. P. Tóth: Multidimensional semi-dispersing billiards: singularities and the fundamental theorem. Annales Henri Poincaré 3 (2002), 451-482.
Zs. Pajor-Gyulai, D. Szász, I. P. Tóth: Billiard models and energy transfer. Proceedings of the International Congress on Math. Physics (Prague, 2009), World Scientific, pp. 6. (invited paper)

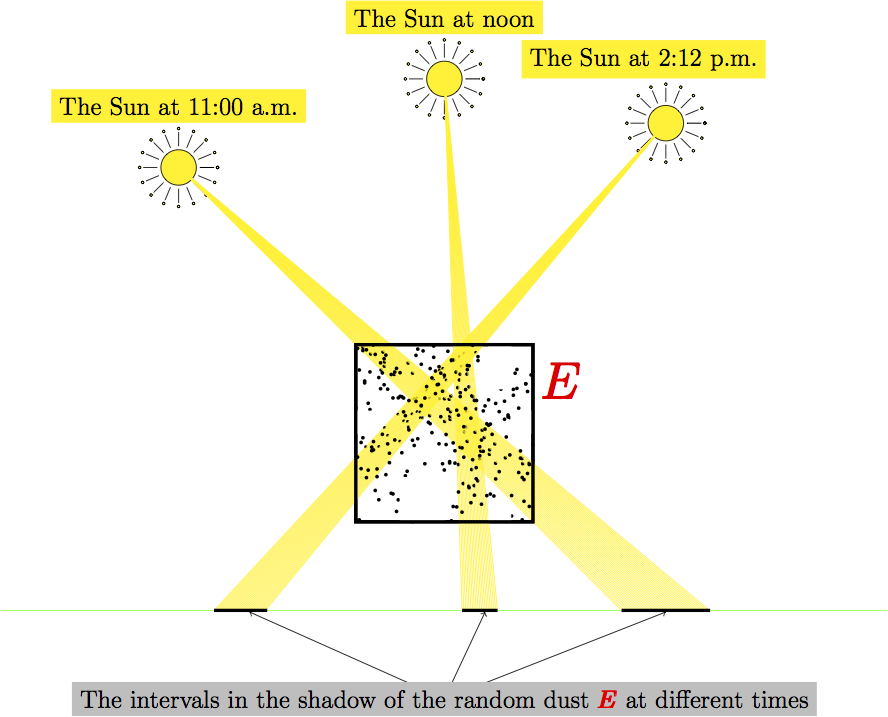
Fractal geometry, dimension theory of dynamical systems, geometric measure theory.

Balázs Bárány, Gergő Kiss, István Kolossváry, Károly Simon, Lajos Vágó

B. Bárány: On the Ledrappier-Young formula for self-affine measures. Preprint, 2015.
B. Bárány, K. Barański, J. Romanowska: On the dimension of the graph of the classical Weierstrass function. Advances in Math. 265 (2014), 32-59.
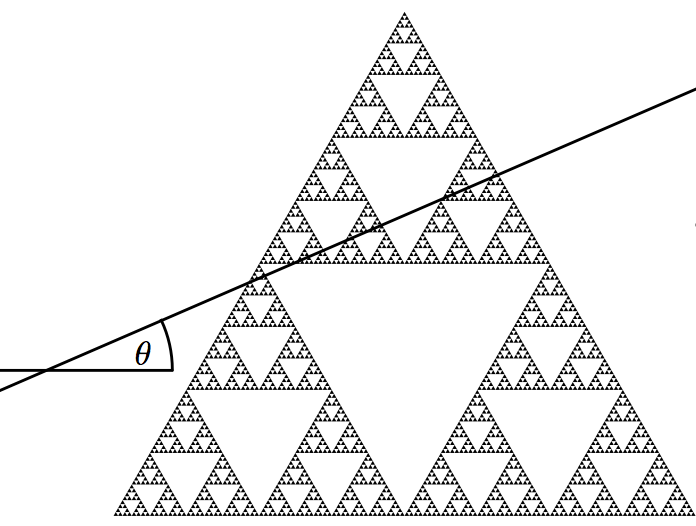
B. Bárány, A. Ferguson, K. Simon: Slicing the Sierpiński gasket. Nonlinearity 25 (2012), 1753-1770.
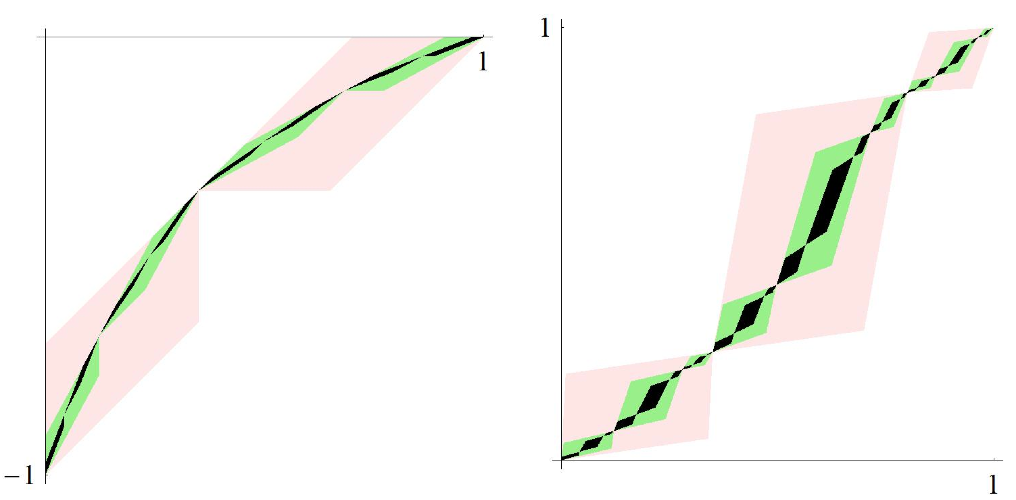
B. Bárány, G. Kiss, I. Kolossváry: On the local Hölder exponents of deRham-like fractal curves. Preprint, 2014.
B. Bárány, I. Kolossváry: On the absolute continuity of the Blackwell measure. J. Stat. Phys., to appear.
V. Harangi, T. Keleti, G. Kiss, P. Maga, A. Máthé, P. Mattila, B. Strenner: How large dimension guarantees a given angle? Monatshefte fur Matematik, to appear.
M Rams, K Simon: Projections of fractal percolations. Ergodic Theory and Dynamical Systems 35 (2015), 530-545.
M Dekking, K Simon, B Székely: The algebraic difference of two random Cantor sets: the Larsson family. The Annals of Probability 39 (2011), 549-586.
M Pollicott, K Simon: The Hausdorff dimension of lambda-expansions with deleted digits. Transactions of the American Mathematical Society 347 (1995), 967-983.
T Jordan, M Pollicott, K Simon: Hausdorff dimension for randomly perturbed self affine attractors. Communications in Mathematical Physics 270 (2007), 519-544.
K Simon, B Solomyak: Hausdorff dimension for horseshoes in R^3. Ergodic Theory and Dynamical Systems 19 (1999), 1343-1363.
K Simon: Hausdorff dimension for non-invertible maps. Ergodic Theory and Dynamical Systems 13 (1993), 199-212.
K. Simon, L. Vágó: Projections of Mandelbrot percolation in higher dimensions. In: Fractals, Wavelets, and their Applications, Springer Proceedings in Mathematics & Statistics 92, 2014, pp. 175-190.

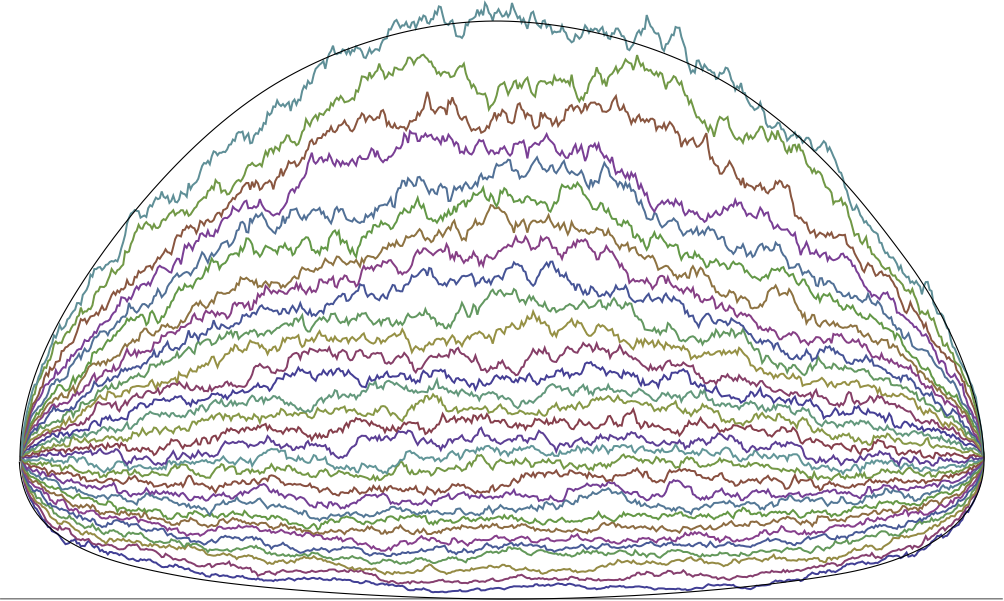
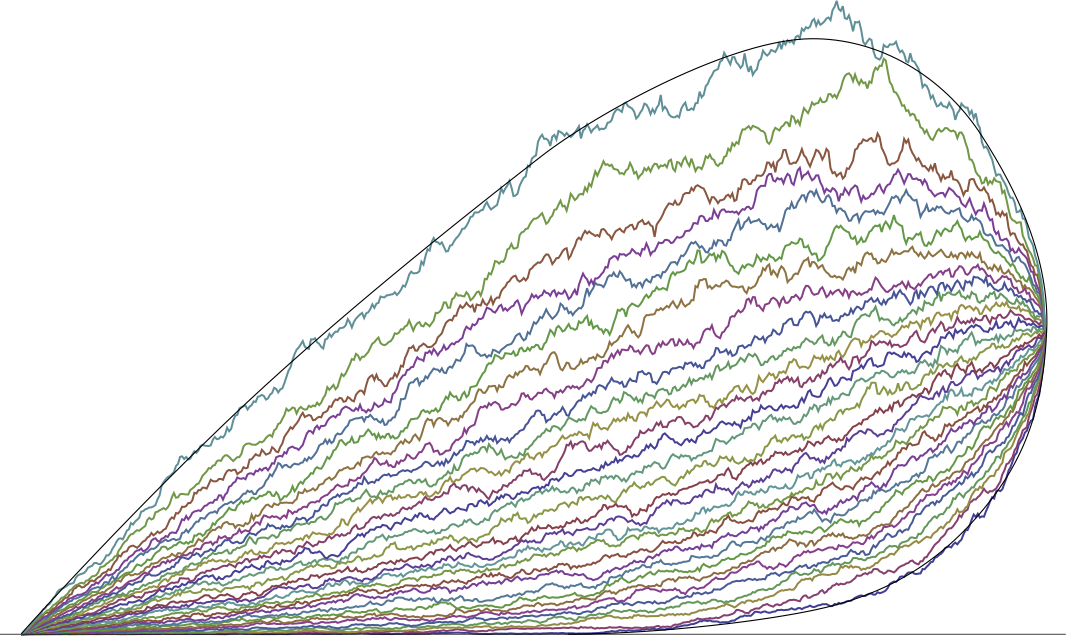
Interacting particle systems, hydrodynamic limits, fluctuations in the KPZ universality class.

Bálint Tóth, Bálint Vető

L. Dumaz, B. Tóth: Marginal densities of the "true" self-repelling motion. Stochastic Processes and their Applications 123 (2013), 1454-1471.
B. Tóth, B. Valkó: Perturbation of singular equilibria of hyperbolic two-component systems: a universal hydrodynamic limit. Communications in Mathematical Physics 256 (2005), 111-157.
J. Fritz, B. Tóth: Derivation of the Leroux system as the hydrodynamic limit of a two-component lattice gas. Communications in Mathematical Physics 249 (2004), 1-27
B. Tóth, B. Valkó: Onsager relations and Eulerian hydrodynamic limit for systems with several conservation laws. Journal of Statistical Physics 112 (2003), 497-521.
B. Tóth, W. Werner: Hydrodynamic equation for a deposition model. In: V. Sidoravicius (editor): In and Out of Equilibrium, Progress in Probability, vol. 51 pp. 229-250, Birkhauser, 2002.
P. L. Ferrari, B. Vető: Tracy-Widom asymptotics for q-TASEP. Ann. Inst. Henri Poincaré Probab. Stat., to appear.
A. Borodin, I. Corwin, P. Ferrari, B. Vető: Height fluctuations for the stationary KPZ equation. Math. Phys. Anal. Geom., to appear.
S. Delvaux, B. Vető: The hard edge tacnode process and the hard edge Pearcey process with non-intersecting squared Bessel paths. Random Matrices Theory Appl., to appear.

Asymptotic behaviour of stohastic processes with long memory. Self-interacting random walks, and random walks in random environment.

Domokos Szász, Bálint Tóth, Bálint Vető

D. Szász, B. Tóth: Dynamical theory of the Brownian particle in a Rayleigh-gas . Journal of Statistical Physics 47 (1987), 681-695.
A. Krámli, D. Szász: Random walks with internal degrees of freedom. Probability Theory and Related Fields 63 (1983), 85-95.
G. Kozma, B. Tóth: Central limit theorem for random walks in divergence-free random drift field: $H_{-1}$ suffices. Preprint, 2014.
A. Erschler, B. Tóth, W. Werner: Stuck walks. Probability Theory and Related Fields 154 (2012), 149-163.
I. Horváth, B. Tóth, B. Vető: Relaxed sector condition. Bulletin of the Institute of Mathematics, Academia Sinica (N.S.) 7 (2012), 463-476.
I. Horváth, B. Tóth, B. Vető: Diffusive limits for ``true'' (or myopic) self-avoiding random walks and self-repellent Brownian polymers in d>=3. Probab. Theory Related Fields 153 (2012), 691-726.
P. Tarres, B. Tóth, B. Valkó: Diffusivity bounds for 1d Brownian polymers. The Annals of Probability 40 (2012), 695-713.
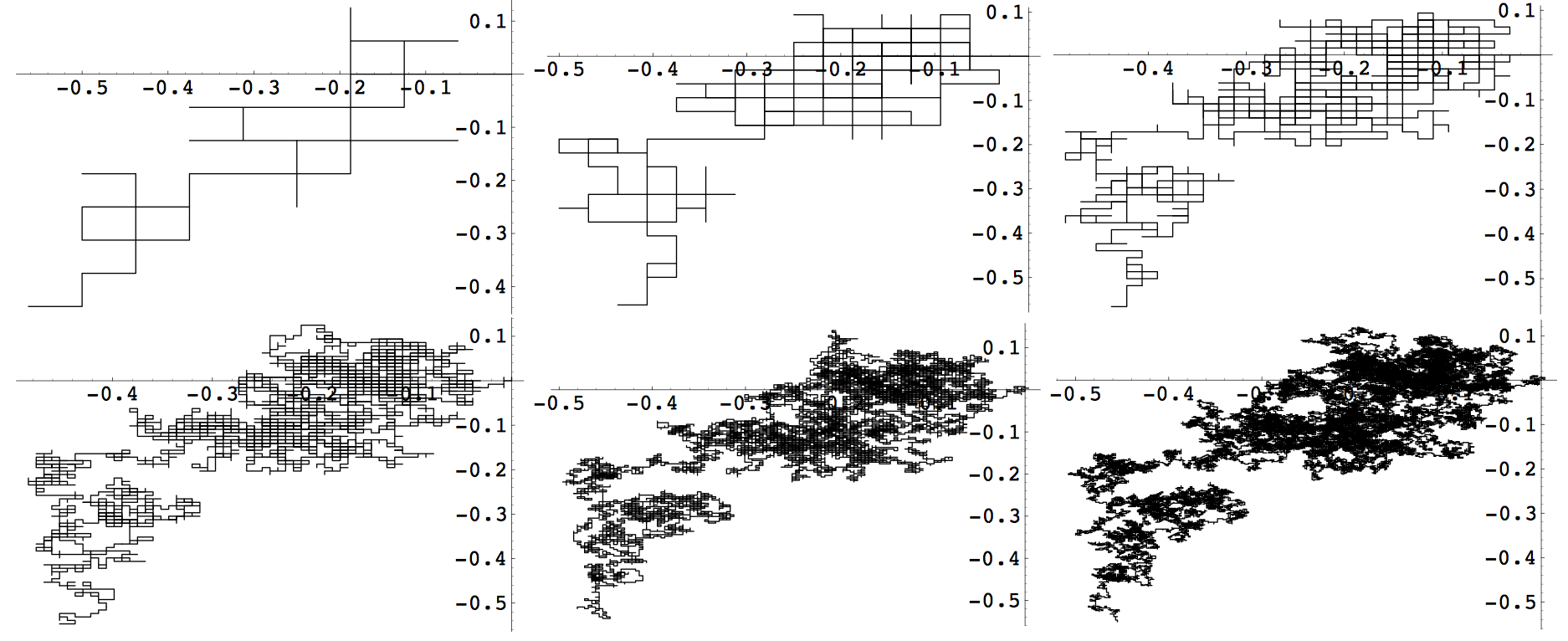
B. Tóth, W. Werner: The true self-repelling motion. Probability Theory and Related Fields 111 (1998), 375-452.
B. Tóth: Generalized Ray-Knight theory and limit theorems for self-interacting random walks. The Annals of Probability 24 (1996), 1324-1367.

Space-time representation of the True Self-Repelling Motion

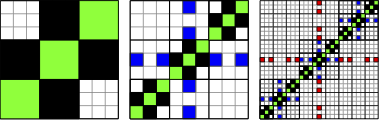
Spectra of graphs and matrices. Cluster analysis by graph theoretical methods. Parametric and semiparametric network models.

Marianna Bolla, Ahmed ElBanna AboZaid.

M. Bolla: Spectral Clustering and Biclustering. Learning Large Graphs and Contingency Tables. Wiley, 2013.
M. Bolla: SVD, discrepancy, and regular structure of contingency tables. Discrete Applied Mathematics 176 (2014), 3-11.
M. Bolla, A. ElBanna AboZaid: Estimating parameters of a multipartite loglinear graph model via the EM algorithm. Preprint, 2014.
M. Bolla: Modularity spectra, eigen-subspaces, and structure of weighted graphs. European Journal of Combinatorics 35 (2014), 105-116.
M. Bolla, K. Friedl, A. Krámli: Singular value decomposition of large random matrices (for two-way classification of microarrays). Journal of Multivariate Analysis 101 (2010) 434-446.
M. Bolla: Recognizing linear structure in noisy matrices. Lin. Alg. Appl. 402 (2005), 228-244.
M. Bolla, G. Tusnády: Spectra and optimal partitions of weighted graphs, Discrete Mathematics 128 (1994), 1-20.

Random graphs and complex networks. Limit theorems and self-organized criticality in dynamical random graph models.

István Kolossváry, Balázs Ráth, Károly Simon, Bálint Tóth, Imre Péter Tóth

I. Kolossváry, J. Komjáthy, L. Vágó: Degrees and distances in random and evolving Apollonian networks
I. Kolossváry, J. Komjáthy: First passage percolation on inhomogeneous random graphs. Advances in Applied Probability, to appear.
I. Kolossváry and B. Ráth: Multigraph limits and exchangeability. Acta Math. Hung. 130 (2011), 1-34.
B. Ráth: Time evolution of dense multigraph limits under edge-conservative preferential attachment dynamics. Random Structures and Algorithms 41 (2012), 365-390.
B. Ráth: Mean field frozen percolation. Journal of Statistical Physics 137 (2009), 459-499.
B. Ráth, B. Tóth: Erdős-Rényi random graphs + forest fires = Self-Organized Criticality. Electronic Journal of Probability 14 (2009), 1290-1327.
A. Rudas, B. Tóth, B. Valkó: Random trees and general branching processes. Random Structures and Algorithms 31 (2007), 186-202.
A. Rudas, I. P. Tóth: Entropy and Hausdorff Dimension in Random Growing Trees. Stochastics and Dynamics 13 (2013), 1250010.
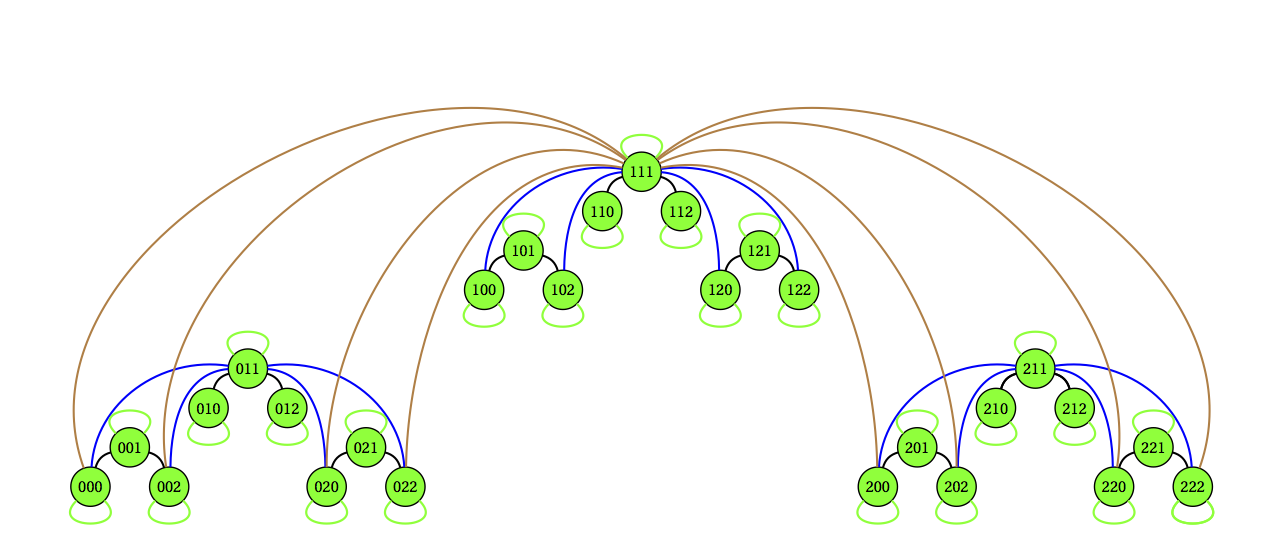
J Komjáthy, K Simon: Generating hierarchial scale-free graphs from fractals. Chaos, Solitons & Fractals 44 (2011), 651-666.

Adjacency matrix of an Erdos-Renyi random graph

Adjacency matrix of a preferential attachment random graph

Adjacency matrix of a preferential attachment random graph, vertices ordered according to degree

Approximating 2-dim Brownian motion by simple random walk

Stochastic analysis, strong approximation and applications

Tamás Szabados

T. Szabados, B. Székely: Stochastic integration based on simple, symmetric random walks. J. Theoret. Probab. 22 (2009), 203-219.
T. Szabados: Strong approximation of fractional Brownian motion by moving averages of simple random walks. Stoch. Proc. Appl. 92 (2001), 31-60.
T. Szabados: An elementary introduction to the Wiener process and stochastic integrals. Studia Sci. Math. Hung. 31 (1996), 249-297

Probabilistic, geometric, analytic aspects of infinite groups.

Gergő Kiss, Gábor Pete

G. Kiss, M. Laczkovich: Linear functional equations, differential operators and spectral synthesis Aequat. Math. 89 (2015), 301-328.
G. Kiss, G. Somlai: Decomposition of balls in R^d. Mathematika, to appear.
G. Kiss, M. Laczkovich: Decomposition of balls into finitely many pieces. Mathematika 57 (2011), 89-107.
V. Nekrashevych, G. Pete: Scale-invariant groups. Groups, Geometry and Dynamics 5 (2011), 139-167.
J. Balogh, Y. Peres, G. Pete: Bootstrap percolation on infinite trees and non-amenable groups. Combinatorics, Probability and Computing 15 (2006), no. 5, 715-730.
G. Pete: Probability and Geometry on Groups. Book in preparation.

A Cayley graph of the integer Heisenberg group

$The adding machine action of \Z on the binary tree$

Number theory: combinatorial and probabilistic aspects. Cryptographic applications.

Tünde Kovács, Csaba Sándor, Gábor Pete

A. Bérczes, L. Hajdu, N. Hirata-Kohno, T. Kovács, A. Pethő: A key exchange protocol based on Diophantine equations and S-integers. JSIAM Letters 6 (2014), 85-88.
K. Győry, T. Kovács, Gy. Péter, Á. Pintér: Equal values of standard counting polynomials. Publicationes Mathematicae 84 (2014), 259-277.
L. Hajdu, T. Kovács: Almost fifth powers in arithmetic progression. Journal of Number Theory 131 (2011), 1912-1923.
L. Hajdu, T. Kovács: Parallel LLL-reduction for bounding the integral solutions of elliptic Diophantine equations. Mathematics of Computation 78 (2009), 1201-1210.
Cs. Sándor: A note on a conjecture of Erdős-Turán. Integers 8 (2008), A30, 4 pp. (electronic)
Cs. Sándor: Partitions of natural numbers and their representation functions. Integers 4 (2004), A18, 5 pp. (electronic)
P. Erdős, G. Rauzy, Cs. Sándor, A. Sárközy: Greedy algorithm, arithmetic progressions, subset sums and divisibility. Paul Erdős memorial collection. Discrete Math. 200 (1999), 119-135.
Y-G. Chen, G. Kun, G. Pete, I. Z. Ruzsa, Á. Timár. Prime values of reducible polynomials, II. Acta Arithmetica, 104 (2002), 117-127.

Information theory. Prediction and nonparametric estimation for stationary processes.

Imre Csiszár, Tamás Kói, Gusztáv Morvai

I. Csiszár and J. Körner. Information Theory: Coding Theorems for Discrete Memoryless Systems, Second Edition. Cambridge University Press, Cambridge, 2011.
I. Csiszár, P. Shields: Information Theory and Statistics: A Tutorial. Foundations and Trends in Communications and Information Theory 1 (2004), 417-528.
L. Farkas, T. Kói: Random access and source-channel coding error exponents for multiple access channels. IEEE Transactions on Information Theory, vol. 61, pp. 3029-3040, Jun. 2015
L. Farkas, T. Kói: On capacity regions of discrete asynchronous multiple access channels. Kybernetika 50 (2014), 1003-1031.
G. Morvai, B. Weiss: A note on prediction for discrete time series. Kybernetika 48 (2012), 809-823. (Editor's Award.)
G. Morvai, B. Weiss: Nonparametric sequential prediction for stationary processes. The Annals of Probability 39 (2011), 1137-1160.
G. Morvai, B. Weiss: Forward estimation for ergodic time series. Ann. Inst. H. Poincaré Probab. Statist. 41 (2005), 859-870. (Prized paper.)

Nonparametric Bayesian statistics.

Botond Szabó

B. T. Szabó, A. W. van der Vaart, J. H. van Zanten: Frequentist coverage of adaptive nonparametric Bayesian credible sets, and Rejoinder to discussion of "Frequentist coverage of adaptive nonparametric Bayesian credible sets." Annals of Statistics, to appear.
B. T. Knapik, B. T. Szabó, A. W. van der Vaart, J. H. van Zanten: Bayes procedures for adaptive inference in nonparametric inverse problems. Probability Theory and Related Fields, to appear.
T. Turányi, T. Nagy, I. Gy. Zsély, M. Cserháti, T. Varga, B. T. Szabó, I. Sedyó, P. T. Kiss, A. Zempléni, H. J. Curran: Determination of rate parameters based on both direct and indirect measurements. International Journal of Chemical Kinetics 44 (2012), 284-302.

Applications of probability theory to biology and chemistry

Béla Barabás, Tamás Szabados

B. Barabás, J. Tóth, Gy. Pályi: Stochastic aspects of asymmetric autocatalysis and absolute asymmetric synthesis. Journal of Mathematical Chemistry 48 (2010), 457-489.
B. Barabás, L. Caglioti, K. Micskei, C. Zucchi, Gy. Pályi: Isotope chirality and asymmetric autocatalysis: a possible entry to biological chirality. Origins of Life and Evolution of the Biosphere 38 (2008), 317-327.
B. Barabás, L. Caglioti, C. Zucchi, M. Maioli, E. Gál, K. Micskei, Gy. Pályi: Violation of distribution symmetry in statistical evaluation of absolute enantioselective synthesis. The Journal of Physical Chemistry B 111 (2007), 11506-11510.
T. Bakács, T. Szabados: A new homeostatic model of the T cell system. Journal of Biological Systems 19 (2011), 299-317.
T Bakács, JN Mehrishi, T Szabados, L Varga, M Szabo, G Tusnády: T cells survey the stability of the self: a testable hypothesis on the homeostatic role of TCR-MHC interactions. International archives of allergy and immunology 144 (2006), 171-182.
T. Szabados, G. Tusnády, L. Varga, T. Bakács: A stochastic model of B cell affinity maturation and a network model of immune memory. Manuscript, 1998.