Previous research projects
Effect of periodically fluctuating flow velocity on an aeroelastic wing model
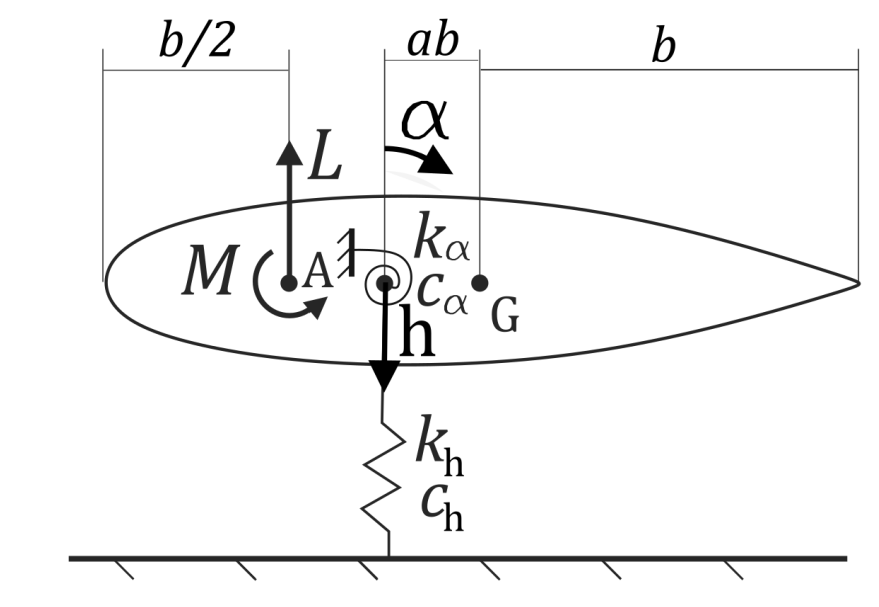
I have carried out a stability analysis for a two degrees of freedom pitch-plunge aeroelastic model with parametric excitation. This corresponds to the forward flight of a helicopter, where the relative wind velocity expierenced by the rotor blades changes periodically. Numerical stability analysis was carried out for several different parametric excitation frequencies. For 2:1 parametric resonance, where the parametric excitation frequency is twice the flutter frequency, an analytic stability analysis was also carried out using perturbation methods. Both the method of multiple scales and the Hill-Bolotin method were applied. The analytic stability boundaries showed a good aggreement with the numerical results.
This figure shows the numerical stability chart. The amount of time it takes for the oscillation amplitude to reach a certain treshold is plotted as a function of the dimensionless rotational velocity of the helicopter rotor \(\delta\) and the dimensionless forward velocity \(\varepsilon\). Red color represents the stable region, blue color represents the unstable region. Using the slider, the ratio of the parametric excitation frequency and the flutter frequency \(\gamma/\Omega_0\) can be changed. At \(\gamma=2\Omega_0\), the analytic stability boundaries are also shown.
\(\gamma/\Omega_0\)