Barkóba
A barkóba két függvényből áll. Az egyik generál egy számot, amelyet egy globális változóba tárol el. Ezt el fogjuk érni a másik függvényből is, amelyet azért hívunk meg, hogy tippeljünk.
| > |
barkobainit:=proc(n::integer)
global secretnumber;
secretnumber := (rand() mod n) + 1;
"OK"
end; |
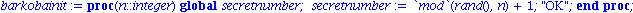
| > |
barkoba:=proc(t::integer)
global secretnumber;
if t > secretnumber then
return("kissebb");
else
if t = secretnumber then
return("gratula");
else
return("nagyobb");
fi;
fi;
end; |


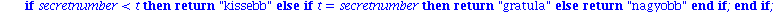

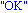
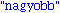
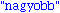

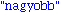
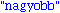
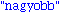

Legnagyobb közös osztó
Euklideszi algoritmus egy rekurzív megvalósítása a következő függvény.
| > |
sajatgcd:=proc(a::integer,b::integer)
if b=0 then a;
else gcd(b,a mod b);
fi;
end; |

Próbaképp a beépített gcd függvény a legnagyobb közös osztót adja vissza

úgy, mint a mi legnagyobb közös oszó számoló függvényünk.

Birthday paradoxon valószínűsége
Az a valószínűség, hogy van két ember, akik ugyanazon a napon születtek az alábbi képlettel számlható:
| > |
birthday2:=proc(n::integer,m::integer)
local i;
1-product((n-i)/n,i=1..m-1);
end; |
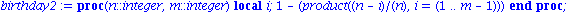
Az alábbi ábrán a vízszintes tengelyt x-szel jelölve azt a valószínűséget látjuk, hogy 365 nap esetén x ember között lesz két olyan, akik ugyanazon a napon születtek.
| > |
with(plots):listplot([seq(evalf(birthday2(365,i)),i=1..50)]); |
Warning, the name changecoords has been redefined
![[Plot]](images/3ora_19.gif)
Warning, the assigned name Group now has a global binding

Szimmetrikus bolyongás
Az alábbi függvény egy lista részletösszegeit írja ki.
| > |
PartialSums([1,1,1,-1,-1,666]); |
![[1, 2, 3, 2, 1, 667]](images/3ora_22.gif)
Vegyünk egy szimmetrikus bolyongást. Minden lépésben 1/2 - 1/2 valószínűséggel lépünk fel és le. A következő képpen valósítjuk meg: létrehozunk egy 10 hosszú listát, amelyben minden elem 50%-os valószínűséggel -1, illetve 1, majd ennek vesszük a részletösszegeit. Így olyan, mintha minden egyes lépés után az előzőhöz vagy hozzáadunk 1-et, vagy kivonunk 1-et.
| > |
listplot(PartialSums([seq(2*(rand() mod 2)-1,i=1..10)])); |
![[Plot]](images/3ora_23.gif)
Növelve a lépések számát megfelelő messziségből egy Brown-mozgást látunk. A Brown-mozgás fontos fizikában (részecskemozgás), pénzügyben (tőzsde), valószínűségszámításban.
| > |
listplot(PartialSums([seq(2*(rand() mod 2)-1,i=1..10000)])); |
![[Plot]](images/3ora_24.gif)
Ha 5-ös Maple-t használunk, akkor nem lesz PartialSums függvényünk, úgyhogy írjunk egyet!
| > |
part:=proc(l::list)
local i,s,r;
r:=array(1..nops(l));
s:=0;
for i from 1 to nops(l) do
s:=s+l[i];
r[i]:=s;
od;
r;
end; |
![part := proc (l::list) local i, s, r; r := array(1 .. nops(l)); s := 0; for i to nops(l) do s := s+l[i]; r[i] := s end do; r end proc](images/3ora_25.gif)
| > |
listplot(part([seq(2*(rand() mod 2)-1,i=1..10000)])); |
![[Plot]](images/3ora_26.gif)
Rajzolási opciók, függvény iterálás
A plot függvény opcióiról segítséget az alábbi módon kérhetünk. Van egy link erre a plot leírásánál legalul.
exp@@2 egy olyan függvény exp(exp( )) függvényt jelöli.
Az exp@@3 pedig az exp 3-szoros iterációját.

Az alábbi grafikonon 1, sin(x), sin(sin(x)), sin(sin(sin(x))), .... látható. A paraméterekkel csak azt érjük el, hogy szebb legyen az ábra.
| > |
listplot([seq(evalf((sin@@n)(1)),n=1..20)],color=red,axes=boxed,labels=[érték,lépésszám],view=[0..21,0..1],style=point,symbol=cross,symbolsize=20); |
![[Plot]](images/3ora_29.gif)
Műveletek listákkal
Egy gyorsabb megadási módja a 10-től 20-ig terjedő számoknak
![l := [10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]](images/3ora_30.gif)
Az 5 prím.
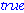
A 6 nem prím.
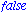
A select egy lista minden egyes elemére lefuttatja az első paraméterként kapott függvényt, és csak azokat hagyja bent, amelyre a függvény true-val tért vissza.
![[11, 13, 17, 19]](images/3ora_33.gif)
A remove ugyanazt csinálja, mint a select, épp ellenkezőleg a true-val visszatérő tagokat dobja el.
![[10, 12, 14, 15, 16, 18, 20]](images/3ora_34.gif)
A függvényt kicserélhetjük egy általunk megírt függvényre, amelyet megadhatunk így
| > |
select(proc(x) if x>15 then true; else false; fi; end, l); |
![[16, 17, 18, 19, 20]](images/3ora_35.gif)
és így is.
| > |
select(x->if x>15 then true; else false; fi, integers); |
![[16, 17, 18, 19, 20]](images/3ora_36.gif)
Vegyünk egy egyszerű listát.
![l := [1, 2, 3, 4]](images/3ora_37.gif)
A Rotate parancs a ListTools csomagban található, a második paraméterben azt kell megadni, hogy hány elemmel fogassa el a listát.
![[2, 3, 4, 1]](images/3ora_38.gif)
A Flatten szétszedi az egymásba ágyazott listákat, és 1 listát készít.
| > |
Flatten([1,2,3,[4,5]]); |
![[1, 2, 3, 4, 5]](images/3ora_39.gif)
Rendezés.
![[1, 2, 3, 4]](images/3ora_40.gif)
Elem vizsgálat.
Fraktálok
Egy kétváltozós függvény:
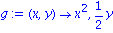
Próbaképp értékeljük ki 1 helyen:
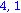
A Sierpinski háromszöget fogjuk kirajzolni. Az elv a következő: a sierpinski függvénynek 3 paramétert adunk: egy l listát, amelyben az eddig kiszámolt pontok lesznek, illetve 3 függvényt, amely az iterált függvényrendszer elemei. Egy 4 elemű sorozattal tér vissza, amelynek első eleme az általa kibővített lista, a többi 3 eleme pedig a függvény változatlanul. Így alkalmas arra, hogy iteráljuk a sierpinski függvényt, hiszen pont olyan típusú kimenete van, mint amilyen típusú bemenete.
| > |
sierpinski:=proc(l,g1,g2,g3)
local i;
[seq([g1(op(l[i]))],i=1..nops(l)),seq([g2(op(l[i]))],i=1..nops(l)),seq([g3(op(l[i]))],i=1..nops(l))],g1,g2,g3;
end; |
![sierpinski := proc (l, g1, g2, g3) local i; [seq([g1(op(l[i]))], i = (1 .. nops(l))), seq([g2(op(l[i]))], i = (1 .. nops(l))), seq([g3(op(l[i]))], i = (1 .. nops(l)))], g1, g2, g3 end proc](images/3ora_44.gif)
Iteráljuk a függvényt 7-szer, és elindítjuk a [0,0] pontból. A legvégén olyan pontokat fog visszaadni, amelyek a [0,0] pontból állíthatóak elő a megadott 3 függvény összesen 7-szeri tetszőleges alkalmazásával.
| > |
plot( (sierpinski@@7)( [[0,0]],(x,y)->(x/2,y/2),(x,y)->(x/2+1/2,y/2),(x,y)->(x/2+1/4,y/2+sqrt(3)/4))[1], style=point, symbol=POINT, scaling=constrained); |
![[Plot]](images/3ora_45.gif)
Általános fraktálszámoló eljárás. A különbség csak annyi, hogy nem 3 függvényt adunk meg neki, hanem egy listát, amelyben függvények vannak.
| > |
fraktal:=proc(l,g)
local i,j;
[seq(seq([g[j](op(l[i]))],i=1..nops(l)),j=1..nops(g))],g;
end proc; |
)], i = (1 .. nops(l))), j = (1 .. nops(g)))], g end proc](images/3ora_46.gif)
Az előző program átírata a fraktal függvényre.
| > |
plot( (fraktal@@7)( [[0,0]],[(x,y)->(x/2,y/2),(x,y)->(x/2+1/2,y/2),(x,y)->(x/2+1/4,y/2+sqrt(3)/4)])[1], style=point, symbol=POINT, scaling=constrained); |
![[Plot]](images/3ora_47.gif)
Más fraktálok is gyorsan kódolhatóak.
| > |
plot( (fraktal@@4)( [[0,0]],[(x,y)->(x/3,y/3),(x,y)->(x/3,y/3+1/3),(x,y)->(x/3,y/3+2/3),(x,y)->(x/3+1/3,y/3),(x,y)->(x/3+2/3,y/3),(x,y)->(x/3+2/3,y/3+1/3),(x,y)->(x/3+2/3,y/3+2/3),(x,y)->(x/3+1/3,y/3+2/3)])[1], style=point, symbol=POINT, scaling=constrained); |
![[Plot]](images/3ora_48.gif)
A véletlenné tételének egy módszere.
| > |
veletlenfraktal:=proc(l,g)
local i,j,ret;
ret:=[];
for j from 1 to nops(g) do
if (rand() mod 3) < 2 then
ret := [op(ret),seq([g[j](op(l[i]))],i=1..nops(l))];
fi;
od;
ret,g;
end proc; |
![veletlenfraktal := proc (l, g) local i, j, ret; ret := []; for j to nops(g) do if `mod`(rand(), 3) < 2 then ret := [op(ret), seq([g[j](op(l[i]))], i = (1 .. nops(l)))] end if end do; ret, g end proc](images/3ora_49.gif)
![veletlenfraktal := proc (l, g) local i, j, ret; ret := []; for j to nops(g) do if `mod`(rand(), 3) < 2 then ret := [op(ret), seq([g[j](op(l[i]))], i = (1 .. nops(l)))] end if end do; ret, g end proc](images/3ora_50.gif)
![veletlenfraktal := proc (l, g) local i, j, ret; ret := []; for j to nops(g) do if `mod`(rand(), 3) < 2 then ret := [op(ret), seq([g[j](op(l[i]))], i = (1 .. nops(l)))] end if end do; ret, g end proc](images/3ora_51.gif)
![veletlenfraktal := proc (l, g) local i, j, ret; ret := []; for j to nops(g) do if `mod`(rand(), 3) < 2 then ret := [op(ret), seq([g[j](op(l[i]))], i = (1 .. nops(l)))] end if end do; ret, g end proc](images/3ora_52.gif)
![veletlenfraktal := proc (l, g) local i, j, ret; ret := []; for j to nops(g) do if `mod`(rand(), 3) < 2 then ret := [op(ret), seq([g[j](op(l[i]))], i = (1 .. nops(l)))] end if end do; ret, g end proc](images/3ora_53.gif)
| > |
plot( (veletlenfraktal@@5)( [[0,0]],[(x,y)->(x/2,y/2),(x,y)->(x/2,y/2+1/2),(x,y)->(x/2+1/2,y/2),(x,y)->(x/2+1/2,y/2+1/2)])[1], style=point, symbol=POINT, scaling=constrained, view=[0..1,0..1]); |
![[Plot]](images/3ora_54.gif)
Ez az igazi véltelenítés. Minden esetben feldob egy érmét, és a véletlentől teszi függővé, hogy az adott iterált függvényt meghívja-e. Rekurzívan oldottam meg, a program teljesen máshogyan fut, mint az eddigiek. Az eddigieknél bonyolultabb, nem gond, ha valaki ezt nem érti.
| > |
veletlenfraktal2:=proc(l,g,n::integer)
local i,j,ret,tr;
if n = 0 then return l; fi;
ret:=[];
for j from 1 to nops(g) do
if (rand() mod 9) < 8 then
tr := veletlenfraktal2(l,g,n-1);
ret := [op(ret),seq([g[j](op(tr[i]))],i=1..nops(tr))];
fi;
od;
ret;
end proc; |
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_55.gif)
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_56.gif)
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_57.gif)
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_58.gif)
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_59.gif)
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_60.gif)
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_61.gif)
![veletlenfraktal2 := proc (l, g, n::integer) local i, j, ret, tr; if n = 0 then return l end if; ret := []; for j to nops(g) do if `mod`(rand(), 9) < 8 then tr := veletlenfraktal2(l, g, n-1); ret := [o...](images/3ora_62.gif)
| > |
plot( veletlenfraktal2( [[0,0]],[(x,y)->(x/2,y/2),(x,y)->(x/2,y/2+1/2),(x,y)->(x/2+1/2,y/2),(x,y)->(x/2+1/2,y/2+1/2)], 6), style=point, symbol=POINT, scaling=constrained,view=[0..1,0..1]); |
![[Plot]](images/3ora_63.gif)
Contourplot
A contourplot-tal szép ábrákat lehet készíteni. A megadott függvény szintvonalait ábrázolja.
| > |
contourplot(sin(x*y),x=-3..3,y=-3..3); |
![[Plot]](images/3ora_64.gif)
Ugyanez 3 dimenzióban.
| > |
contourplot3d(exp(-(2*x^2+y^2)/2),x=-2..2,y=-2..2); |
![[Plot]](images/3ora_65.gif)
| > |
plot3d(0.3*x^3-x+y^2, x=-2..2, y=-2..2, axes=box, color=0.3*x^3-x+y^2, title=Köbös); |
![[Plot]](images/3ora_66.gif)
| > |
plot3d(sin(x^2+y^2),x=-2.5..2.5,y=-2.5..2.5, axes=box, style=patchcontour); |
![[Plot]](images/3ora_67.gif)
Pollard faktorizáló módszere
Azoknak ajánlom a következő programot, akik már találkoztak Pollard faktorizáló módszerével.
| > |
Pollard:=proc(n::integer,lim::integer)
local i,x,y,k,d;
i:=1;
x[1]:=(rand() mod n);
y:=x[1];
k:=2;
while i < lim do
i:=i+1;
x[i]:= ((x[i-1]^2-1) mod n);
d:=igcd(y-x[i],n);
if d<>1 and d<>n then
return(d); fi;
if i=k then
y:=x[i];
k:=2*k;
fi;
od;
"Nem sikerült"
end; |
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_68.gif)
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_69.gif)
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_70.gif)
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_71.gif)
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_72.gif)
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_73.gif)
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_74.gif)
![Pollard := proc (n::integer, lim::integer) local i, x, y, k, d; i := 1; x[1] := `mod`(rand(), n); y := x[1]; k := 2; while i < lim do i := i+1; x[i] := `mod`(x[i-1]^2-1, n); d := igcd(y-x[i], n); if d...](images/3ora_75.gif)
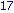
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Plot]](images/3ora_19.gif)
![[Plot]](images/3ora_23.gif)
![[Plot]](images/3ora_24.gif)
![[Plot]](images/3ora_26.gif)
![[Plot]](images/3ora_29.gif)
![[Plot]](images/3ora_45.gif)
![[Plot]](images/3ora_47.gif)
![[Plot]](images/3ora_48.gif)
![[Plot]](images/3ora_54.gif)
![[Plot]](images/3ora_63.gif)
![[Plot]](images/3ora_64.gif)
![[Plot]](images/3ora_65.gif)
![[Plot]](images/3ora_66.gif)
![[Plot]](images/3ora_67.gif)