A témalabor keretében felújítási folyamatokkal foglalkozom. Az előző félévben a prezentációhoz készítettem pár képet és videót, amik segítségével könnyebb megérteni az elméletet. Ezeken szimulációk, és olyan eloszlás- és sűrűségfüggvények vannak, amikről beszéltem a témabeszámolóm alkalmával. Ebben a félévben a Kötelezően választható szemináriumra kiegészítettem a már meglévő példát, és bemutattam az előadáson. Ezeket írom most le. A képletek hiányáért előre is elnézést kérek. A célom az volt, hogy a honlapomra felkerüljön az anyag, és itt pedig nem tudok könnyen képleteket használni. A videók XViD kodekkel kódoltak, ez most elterjedt formátum.
A példa speciális lesz abban az értelemben, hogy az alapeloszlás abszolút folytonos lesz, így természetesen nem aritmetikus, tehát minden aszimptotikával foglalkozó tétel teljesülni fog. Továbbá 1-nél 1 valószínűséggel kisebb, ezzel is segítve az aszimptotikus viselkedés minnél hamarabbi megjelenését. "Puklis" sűrűségfüggvényt választottam, mert így lehet látni az időbeli változás során a lecsengéseket:
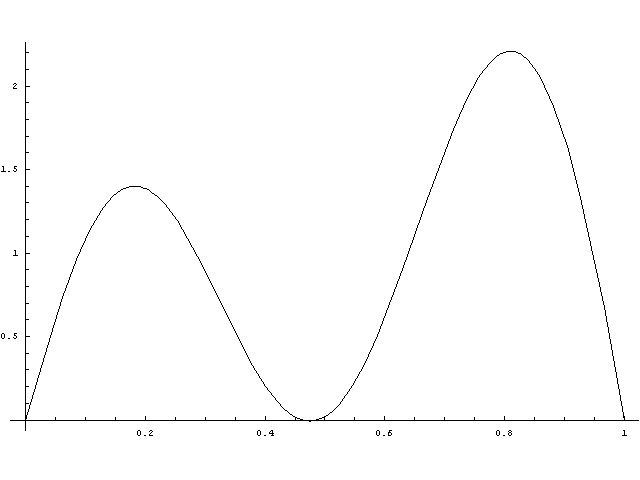
Egy realizáció a fenti eloszlásból generált felújítási folyamatra:
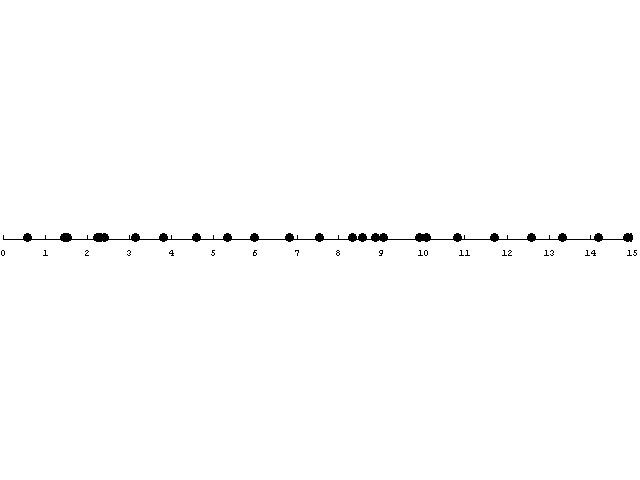
Véletlenül sem gondoljuk azt, hogy ez úgy néz ki, mintha majdnem Poisson pontfolyamat lenne. Összehasonlítás képpen ilyen egy Poisson folyamat.
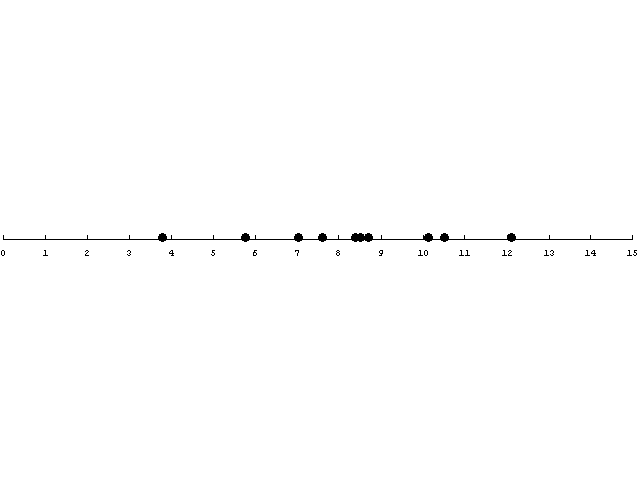
Felsorolás szintjén az első pár konvolúció:
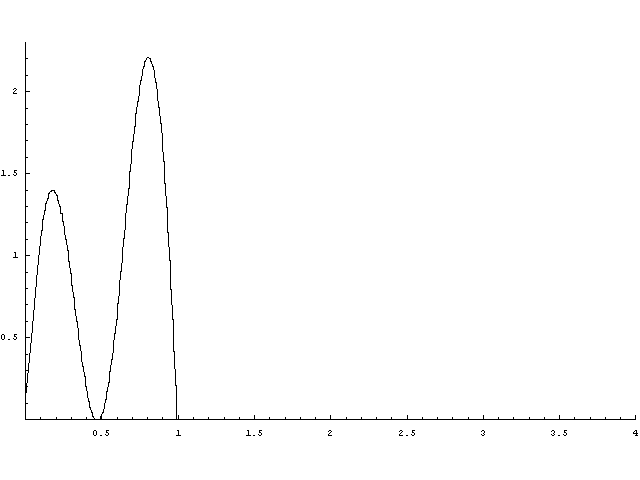
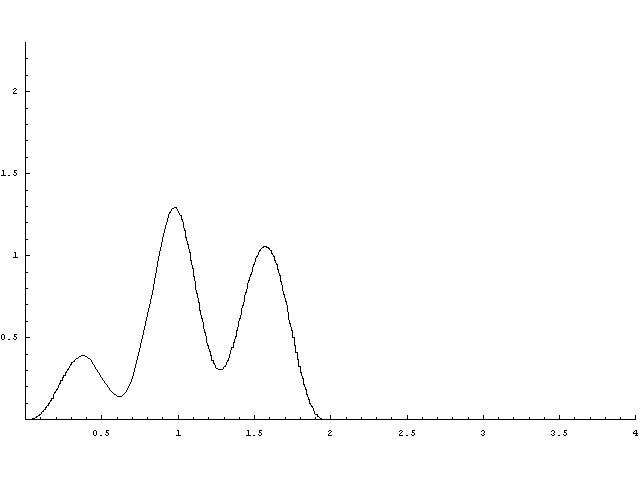
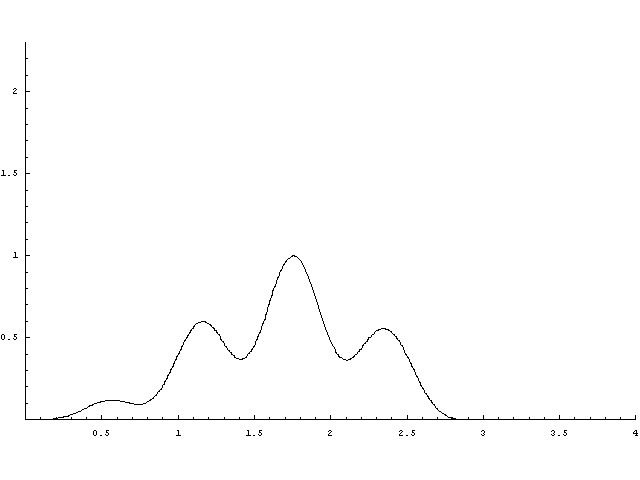
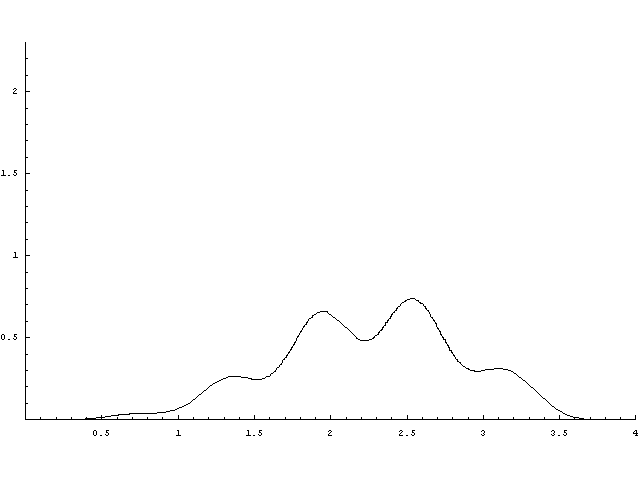
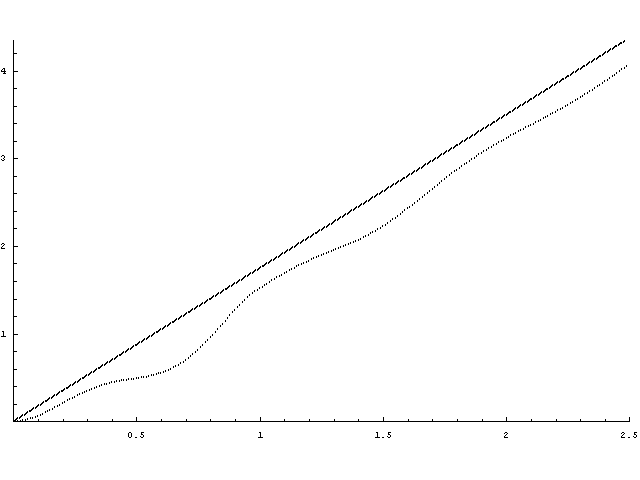
A folymat felújítási függvénye alább látható. Az órán gyakorlatilag mindent vettük róla, hogy aszimptotikusan t/E(X), és a t/E(X)-től vett távolságának határértékét is tudjuk. A második ábrán berajzoltam t/E(X) egyenest.
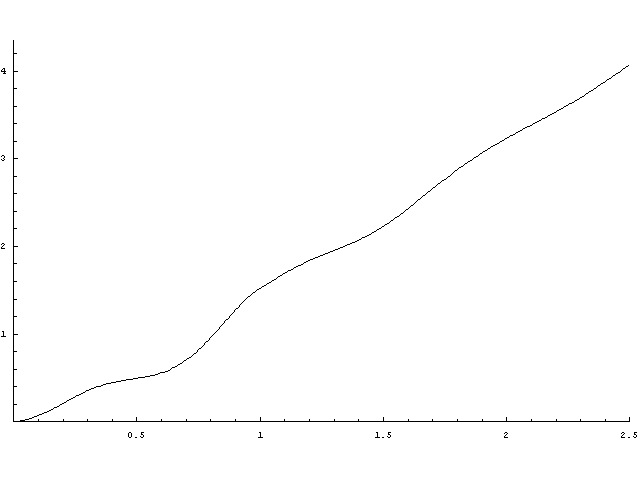
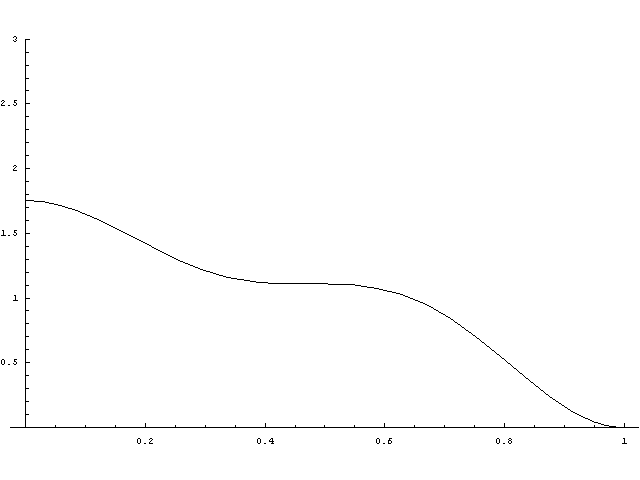
Gamma_t -vel jelöltük a t-től a következő pontig szükséges idő eloszlását. Képletekkel: S_{N(t)+1}-t=Gamma_t. Az alábbi videóban ennek a sűrűségfüggvényét ábrázolom, miközben t értéke növekszik. Természetesen a videó elején az alapeloszlás sűrűségfüggvényét látjuk, hiszen t=0 -ban ez az első pont eloszlásával egyezik meg. Amint t növekszik az ábra balra csúszik, hiszen közel 1 valószínűséggel nem történik esemény 0 és t között. Nagyobb t értékekre azonban egyre jobban kezdi elérni az aszimptotikus határt.
VIDEÓAz aszimtotikus határérték sűrűségfüggvénye ( (1-F(x))/E(X) integrálja 0-tól t-ig):
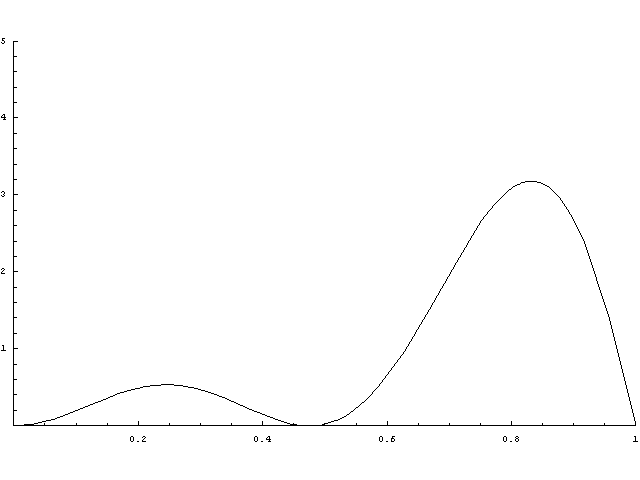
Az előzőekhez hasonlóan nézhetjük az előző eseménytől eltelt idő eloszlását. Képletekkel: t-S_{N(t)}. Az alábbi videóban ennek a sűrűségfüggvényét ábrázolom, miközben t értéke növekszik. t kisebb, mint 1 értékekre nem abszolút folytonos az eloszlás, ott csak az abszolút folytonos résszel foglalkozom. Az aszimptotius határ természetesen ugyanaz lesz, mint az előző példában. Remek gyakorlás felírni az elző pont eloszlását a következő pont eloszlásával.
VIDEÓA t időpontnál lévő intervallum hossza t=0-ra megegyezik az első pont eloszlásával. Kis t-re szakad, mivel a t-nél kisebb értékek a grafikonon azt jelentik, hogy t időpontnál egy t-nél kisebb intervallum van, azaz a 2t-ig legalább két eseménynek is kellett történnie, amire kicsi az esély. Természetesen is sűrűségfüggvényt fogunk ábrázolni.
VIDEÓAz aszimtotikus határérték az x f(x) sűrűségfüggvény lesz lenormálva:
A fenti ábrákat, grafikonokat Mathematicával készítettem. A fájl letölthető. Mindent részletesen dokumentáltam, bár szokásom, hogy szép hosszú összetett függvényeket írok, amik jelentősen rontják az olvasást. Nem használtam Laplace transzformáltat benne, csak elemi valószínűségszámítási megfontolásokat.
Mathematica fájl