Kiindulási pontunk, mint általában, most is egy véletlen kísérlet a hozzá tartozó valószínűségi mezővel és az azon értelmezett valószínűségi mértékkel. Tegyük fel, hogy , egy a kísérletünktől függő, értékű valószínűségi változó. Ebben a részben azt szeretnénk megérteni, milyen az feltétel melletti feltételes valószínűségi mérték (természetesen ). Tehát ha egy esemény, akkor szeretnénk definiálni a
feltételes valószínűséget. Mint látni fogjuk, ha diszkrét eloszlású, akkor ehhez semmilyen új fogalmat nem kell bevezetnünk, a már tárgyalt feltételes valószínűség elegendő. Ha viszont folytonos eloszlású, akkor egészen más megközelítésre lesz szükségünk.
Tegyük fel, hogy diszkrét eloszlású valamilyen valószínűségi súlyfüggvénnyel. Így megszámlálható, és feltehetjük, hogy amint
Igazoljuk, hogy ha egy, a kísérletünktől függő esemény, akkor
Igazoljuk, hogy ha egy esemény, és egy részhalmaza, akkor
Megfordítva, a fenti feladatok egyértelműen meghatározzák a feltétel melletti feltételes valószínűségeket:
Tegyük fel, hogy az elemeken és eseményeken értelmezett függvényre
Igazoljuk, hogy minden -re és minden eseményre!
Legyen most folytonos eloszlású az halmazon valószínűségi sűrűségfüggvénnyel. Tegyük fel, hogy amint . A diszkrét esettel ellentétben nem használhatjuk egyszerűen a már megismert feltételes valószínűséget arra, hogy az halmaz feltétel melletti feltételes valószínűségét definiáljuk, hiszen a feltétel valószínűsége minden -re nulla. Azonban intuitívan érezzük, hogy ennek a feltételnek is van értelme. Ha például elvégzünk egy kísérletet, akkor felvesz valamilyen értéket (aminek a priori nulla volt a valószínűsége), és nyilván ha már tudjuk, hogy bekövetkezett, ez módosíthatja tetszőleges esemény bekövetkezésének valószínűségét. Természetes ötletként adódik, hogy a diszkrét esetben bizonyított állítás megfelelőjét most definícióként használjuk. Tehát legyen
olyan, hogy minden (mérhető) , -beli részhalmazra
Most fogadjuk el, hogy definiálható úgy, hogy kielégítse a fenti feltételt (erre a kérdésre még vissza fogunk térni a Várható érték fejezet Feltételes várható érték című részében).
Legyen ismét egy valószínűségi változó és egy esemény. Az előző két részben tárgyaltak alapján kiszámíthatjuk valószínűségét úgy, hogy értékére, mint feltételre gondolunk, akár a diszkrét, akár a folytonos esetben:
A Bayes tétel (melyet Thomas Bayes-ről neveztek el) feltételes valószínűségi súly-, vagy sűrűségfüggvényére ad egy formulát az feltétel mellett. Ehhez az súly-, vagy sűrűségfüggvényét és feltétel melletti feltételes valószínűségét használja:
Legyen valószínűségi súly-, vagy sűrűségfüggvénye és egy esemény, melyre . Igazoljuk, hogy valószínűségi súly- illetve sűrűségfüggvénye az feltétel mellett a következő (az első formula a diszkrét, a második a folytonos esetre érvényes):
A Bayes tételben -t nevezik a priori súly-, vagy sűrűségfüggvényének, pedig a posteriori súly-, vagy sűrűségfüggvénynek (az feltétel mellett). Vegyük továbbá észre, hogy feltétel melletti feltételes valószínűségi súly-, illetve sűrűségfüggvénye arányos a értékkel, a nevezőben szereplő összeg, vagy integrál csak egy normáló konstans.
A fenti definíciók és eredmények természetesen abban a speciális esetben is érvényesek, amikor az halmazt egy másik valószínűségi változóval definiáljuk. Legyen tehát egy értékű valószínűségi változó. Ekkor az pár is egy valószínűségi változó, amely az szorzathalmazban veszi fel az értékeit. Tegyük fel, hogy (együttes) valószínűségi súly-, vagy sűrűségfüggvénye . (Speciálisan feltesszük, hogy mindkét komponens diszkrét eloszlású, vagy mindkettő folytonos, és létezik sűrűségfüggvényük is, esetleg kevert eloszlásúak, azaz az egyik komponens diszkrét, a másik sűrűségfüggvénnyel bíró folytonos eloszlású.) Mint korábban, jelölje most is az változó súly-, vagy sűrűségfüggvényét, és tegyük fel, hogy amint .
Igazoljuk, hogy a következő függvény egy valószínűségi súly-, vagy sűrűségfüggvény amint , minden -re:
A következő feladatban belátjuk, hogy az változó feltételes súly-, vagy sűrűségfüggvénye az feltétel mellet.
Igazoljuk az alábbi állításokat. Az első esetben tegyük fel, hogy diszkrét, a másodikban pedig, hogy folytonos eloszlású. Tetszőleges esetén
A következő tétel a súly-, illetve sűrűségfüggvényekre vonatkozó Bayes tétel. A korábbi jelöléseket használjuk, és bevezetünk egy új jelölést: legyen feltételes valószínűségi súly-, vagy sűrűségfüggvénye az helyen a feltétel mellett ().
Igazoljuk az alábbi állításokat. Az első esetben tegyük fel, hogy diszkrét, a másodikban pedig, hogy folytonos eloszlású.
A Bayes tételben -t nevezik a prior súly-, vagy sűrűségfüggvényének, pedig a posteriori súly-, vagy sűrűségfüggvénynek (az feltétel mellett). Vegyük továbbá észre, hogy feltétel melletti feltételes valószínűségi súly-, illetve sűrűségfüggvénye arányos a értékkel, a nevezőben szereplő összeg, vagy integrál csak egy normáló konstans.
Szemléletesen és akkor függetlenek, ha a feltételes eloszlások megegyeznek a feltétel nélküli eloszlásokkal (tehát az egyik ismerete nem módosítja a másik eloszlását).
Igazoljuk, hogy az alábbiak ekvivalensek:
Feltételes eloszlásokat gyakran használnak olyan esetekben, amikor egy adott eloszlás paraméterét véletlenítjük. Lássunk erre néhány példát!
Feldobtunk két hagyományos, igazságos kockát, és a dobott számokat -vel jelöltük. Legyen a dobott számok minimuma, pedig a dobott számok maximuma.
A kocka- és érmedobás kísérletében először feldobunk egy igazságos kockát, majd egy pénzérmét annyiszor dobunk fel, amennyi a kockadobás eredménye. Legyen a kockával dobott szám, pedig az érmével dobott fejek száma.
A kocka- és érmedobás kísérletben válasszunk egy igazságos kockát és egy igazságos érmét!
Az érme- és kockadobás kísérletében először feldobunk egy szabályos pénzérmét, majd ha írást kaptunk, egy hagyományos, igazságos kockát dobunk fel, ha pedig fejet kaptunk, egy egy-hat irányban lapos kockát dobunk fel. Ez utóbbi az 1 és a 6 oldalait valószínűséggel, a többi oldalát valószínűséggel mutatja. Jelölje az érmedobás eredményét (0 jelöli az írást, 1 a fejet), pedig a kockadobás eredményét.
Az érme- és kockadobás kísérletében állítsuk be az előző feladat paramétereit!
Tegyük fel, hogy egy dobozban 12 érme van, ezek közül 5 igazságos, 4 cinkelt, ezek valószínűséggel mutatnak fejet, a maradék 3 érmének pedig mindkét oldala fej. Kiválasztunk egy érmét a dobozból, és azt feldobjuk kétszer. Jelölje azt a (véletlentől függő) valószínűséget, amivel a kiválasztott érme fejet mutat, pedig a dobott fejek számát!
Tegyük fel, hogy a valószínűségi változó sűrűségfüggvénye . Ez egy eleme a béta eloszláscsaládnak; a béta eloszlásokat részletesen a Nevezetes eloszlások fejezetben tárgyaljuk. Adott esetén háromszor feldobunk egy érmét, amely valószínűséggel mutat fejet. Jelölje a dobott fejek számát!
Hasonlítsuk össze a 14. feladatot a 15. feladattal! Az utóbbira gondolhatunk úgy, mintha olyan dobozból választottunk volna egy érmét, amelyben végtelen sok típusú érme van.
Egy dobozban 5 villanykörte van, amelyeket megszámoztak egytől ötig. Az -edik villanykörte élettartama (hónapokban kifejezve) exponenciális eloszlású paraméterrel. Kiválasztunk véletlenszerűen egy villanykörtét, és azt becsavarjuk egy foglalatba.
Legyen Poisson eloszlású 1 paraméterrel, és adott esetén binomiális eloszlású és paraméterekkel.
Legyen egyenletes eloszlású az halmazon, és ha , akkor egyenletes eloszlású a intervallumon!
Legyen az pár együttes sűrűségfüggvénye , amint .
Legyen az pár együttes sűrűségfüggvénye , amint .
Legyen az pár együttes sűrűségfüggvénye , amint .
Legyen az pár együttes sűrűségfüggvénye , amint .
Legyen az pár együttes sűrűségfüggvénye , amint .
Legyen egyenletes eloszlású a intervallumon, és ha , akkor egyenletes eloszlású -en.
Elevenítsük fel, hogy mi is a standard (Lebesgue) mérték -en:
Speciálisan, a hosszt méri -en, a területet -n, pedig a térfogatot -n.
Tegyük fel, hogy értékű, értékű úgy, hogy egyenletes eloszlású az halmazon. Vagyis az pár együttes sűrűségfüggvénye
Legyenek és projekciói (vagy más szóval vetületei) -re illetve -ra, azaz:
Ezután definiáljuk az és az pontban vett szeleteket:
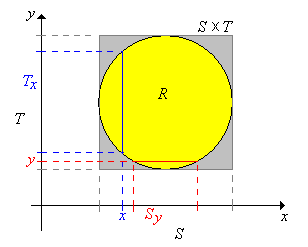
Az Együttes eloszlásokról szóló fejezetben láttuk, hogy annak ellenére, hogy egyenletes eloszlású, és marginális eloszlásai általában nem egyenletesek. Azonban a feltételes eloszlások mindig egyenletesek, ezt igazoljuk a következő feladatban.
Igazoljuk, hogy
A lenti esetek mindegyikében határozzuk meg mindkét valószínűségi változó feltételes eloszlását, és döntsük el, hogy függetlenek-e a változók:
A kétváltozós egyenletes eloszlás kísérletében szimuláljunk 5000 kísérletet (frissítsük az ábrát minden tizedik után) az alábbi esetek mindegyikében. Figyeljük meg a kapott pontfelhőt, és vázoljuk a marginális empirikus sűrűségfüggvényeket! Vessük össze a kapott szimulációs eredményeket az előző feladatokban kapott elméleti eredményekkel!
Legyen az vektor értékű valószínűségi változó egyenletes eloszlású az halmazon!
Az előző, Együttes eloszlások fejezetben tárgyaltuk a (többváltozós) hipergeometrikus eloszlásokat. Ugyanúgy, mint akkor, tegyük fel, hogy darab tárgyunk van, amelyek mindegyike négy különböző típusú lehet. Első típusú darab, második típusú darab, harmadik típusú darab és nulladik típusú darab. Az , és paraméterek természetesen nemnegatív egészek, továbbá . Véletlenszerűen, visszatevés nélkül kiválasztunk tárgyat. Jelölje a kiválasztott első, második és harmadik típusba tartozó tárgyak számát , és . Így a nulladik típusú tárgyakból darabot választottunk ki. Az alábbi feladatok ilyen esetekkel foglalkoznak, legyenek mindenütt az , , számok nemnegatív egészek!
Kombinatorikus és analitikus érvelésekkel is igazoljuk, hogy az pár feltételes eloszlása a feltétel mellett hipergeometrikus eloszlású az alábbi súlyfüggvénnyel. A kombinatorikus érvelésben tekintsünk a kísérletre úgy, mintha elemű véletlen mintát vennénk egy elemű halmazból, amelyek között darab egyes típusú, darab kettes típusú, darab pedig nullás típusú.
Kombinatorikus és analitikus érvelésekkel is igazoljuk, hogy feltételes eloszlása a , feltétel mellett hipergeometrikus eloszlású az alábbi súlyfüggvénnyel. A kombinatorikus érvelésben tekintsünk a kísérletre úgy, mintha elemű véletlen mintát vennénk egy elemű halmazból, amelyek között darab egyes típusú, darab pedig nullás típusú
A fenti feladatok eredményei természetes módon általánosíthatóak több változó esetére. Így kapjuk, hogy egy hipergeometrikus eloszlású véletlen vektor néhány koordinátájának feltételes eloszlása (feltéve, hogy ismerjük a többi koordináta értékét) szintén hipergeometrikus eloszlású. A hipergeometrikus eloszlásról és a többváltozós hipergeometrikus eloszlásról részletes leírást a Véges mintavételezési eljárások fejezetben olvashatunk.
Mint már korábban is tárgyaltuk, a bridzs kísérletben visszatevés nélkül választunk 13 lapot egy hagyományos, 52 lapos franciakártya pakliból. Legyen , és a kiválasztott pikkek, kőrök és kárók száma. Határozzuk meg az alábbi valószínűségi változók valószínűségi súlyfüggvényét:
Az előző, Együttes eloszlások fejezetben tárgyaltuk a multinomiális kísérleteket. Ugyanúgy, mint akkor, tekintsünk most is független kísérleteket, ahol minden kísérlet kimenetele négyféle lehet. Mindegyik kísérletnél az 1. kimenetel , a 2. kimenetel , a 3. kimenetel , a 0. kimenetel pedig paraméterrel következik be. Természetesen a , és paraméterek olyan nemnegatív számok, hogy . Az kísérlet során jelölje az 1 kimenetelű események számát , a 2 kimenetelek számát , a 3 kimenetelek számát pedig . Ekkor a 0. kimenetelek száma . Az alábbi feladatokban legyenek , és nemnegatív egészek.
Valószínűségszámítási és analitikus érveléssel is igazoljuk, hogy feltételes eloszlása a feltétel mellett multinomiális, méghozzá az alábbi súlyfüggvénnyel. A valószínűségszámítási érvelés lényegi része az az észrevétel, hogy a kísérletre tekinthetünk úgy, mint független kísérletre, ahol az 1. kimenetel valószínűsége mindig , a második kimenetelé pedig .
Valószínűségszámítási és analitikus érveléssel is igazoljuk, hogy feltételes eloszlása a és feltételek mellett binomiális az alábbi súlyfüggvénnyel. A valószínűségszámítási érvelés lényegi része az az észrevétel, hogy a kísérletre tekinthetünk úgy, mint független kísérletre, ahol az 1. kimenetel valószínűsége mindig .
Az eredmények természetes módon általánosíthatók olyan multinomiális kísérletekre, ahol tetszőleges számú kimenetel lehetséges. Ez esetben is igaz lesz, hogy egy multinomiális eloszlású vektor néhány komponensének feltételes eloszlása a többi komponens ismerete mellett multinomiális. A binomiális eloszlásról és a multinomiális eloszlásról részletesebben a Bernoulli kísérletekről szóló fejezetben olvashatunk.
Az egy-hat irányban lapos kocka egy olyan hatoldalú dobókocka, amelyet ha feldobnak, valószínűséggel mutat egyet vagy hatot, valószínűséggel pedig kettőt, hármat, négyet vagy ötöt. Feldobtunk egy ilyen kockát ötvenszer, és -vel jelöltük azt, hogy hányszor dobtuk az számot (). Határozzuk meg az alábbi valószínűségi változók súlyfüggvényét:
Legyen az valószínűségi változó pár sűrűségfüggvénye a következő:
Legyen az valószínűségi változó pár sűrűségfüggvénye a következő:
Az előző két példában adott együttes eloszlás a kétváltozós normális eloszlás speciális esetei. Mint láthattuk, ilyenkor a feltételes eloszlások is normálisak. Normális eloszlást nagyon gyakran alkalmaznak a gyakorlatban, például hibával terhelt mérési eredmények modellezésére. A kétváltozós normális eloszlásról részletesen a Nevezetes eloszlások fejezetben olvashatunk.
Legyenek és mint fent, és tegyük fel, hogy egy valószínűségi mérték -n minden -re. Legyen továbbá egy valószínűségi súly-, vagy sűrűségfüggvény -en. Ekkor kaphatunk egy új eloszlást -n úgy, hogy -vel súlyozzuk a fenti eloszlásokat . Így egy keverék eloszlást kapunk.
Először tegyük fel, hogy megszámlálható, pedig egy diszkrét eloszlás súlyfüggvénye -en. Igazoljuk, hogy az alább definiált egy valószínűségi mérték -n:
Az előző feladat jelölései mellett tegyük fel, hogy egy diszkrét (folytonos) eloszlás, melynek súlyfüggvénye (sűrűségfüggvénye) minden -re. Igazoljuk, hogy ekkor is diszkrét (folytonos) eloszlás, melynek súlyfüggvénye (sűrűségfüggvénye) az alábbi függvény:
Tegyük fel most, hogy és egy folytonos eloszlás valószínűségi sűrűségfüggvénye -en. Igazoljuk, hogy az alább definiált egy valószínűségi mérték -n:
Az előző feladat jelölései mellett tegyük fel, hogy egy diszkrét (folytonos) eloszlás, melynek súlyfüggvénye (sűrűségfüggvénye) minden -re. Igazoljuk, hogy ekkor is diszkrét (folytonos) eloszlás, melynek súlyfüggvénye (sűrűségfüggvénye) az alábbi függvény:
A fenti két esetben azt mondjuk, hogy a eloszlás a eloszlások szerint vett keveréke.
Mint látható, valószínűségi eloszlások keverékét akkor is definiálhatjuk, ha a megfelelő valószínűségi változók különböző valószínűségi mezőkön vannak értelmezve. Természetesen lehetnek közös valószínűségi mezőn is, ekkor a feltételes eloszlással rokon fogalmat kapunk. Legyenek ugyanis és valamilyen kísérlettől függő, illetve értékű valószínűségi változók. Tegyük fel, hogy diszkrét vagy folytonos eloszlású, súly-, vagy sűrűségfüggvénnyel. Ekkor a következő feladat állítása igaz (ami nem más, mint a már jól ismert teljes valószínűség tétele).
Igazoljuk, hogy eloszlása nem más, mint feltételes eloszlásainak keveréke az feltételek mellett, ahol , és a keveréket a súly-, vagy sűrűségfüggvénnyel állítjuk elő.
Tegyük fel, hogy egy értékű kevert eloszlású valószínűségi változó (azaz van diszkrét és folytonos komponense). Igazoljuk, hogy eloszlása egy diszkrét és egy folytonos eloszlás fenti értelemben vett keveréke!